46.贪心算法之二:做个好秘书,会议安排问题
Posted 和孩子一起学Python
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了46.贪心算法之二:做个好秘书,会议安排问题相关的知识,希望对你有一定的参考价值。
以会议安排问题为例,进一步理解贪心算法“当前最优”的含义。
上一篇,阿里巴巴又一次偷偷溜进了大盗们藏宝藏的山洞,这次他在山洞里看到很多箱子,箱子里装满了各种沙子状的贵重金属,比如金沙,银沙等等。
每个箱子上也贴上了标签,写着这个箱子里宝物的总重量(不含箱子重量)和总价值。
如果阿里巴巴有足够多不计重量的布口袋,在小毛驴承重有限的前提下,如何拿走价值最多的宝物?
这个问题的贪心策略是什么?
很显然,每一步的“当前最好”的选择是拿单价最高的宝物。
第1步,利用random模块,创建n个随机重量和价值的箱子。
import random
s = []
n = 10
for i in range(n):
s.append([random.randint(1, 20), random.randint(5, 1000)])
print(s)
第2步,对n个箱子按宝物的单价从大到小重新排序。
比如第1步得到如下10个随机重量和价值的箱子,怎么对它们按单价重新排序呢?

在《16.快速掌握Python列表类:Python列表类函数归纳总结》里,我们介绍了Python列表类的重用函数,其中sort() 函数可以对列表里的元素进行排序。
比如
list1 = [10,3,18,4,9]
调用sort() 函数之后
list1.sort()
列表里的元素就变成了 [3,4,9,10,18]
但现在我们列表里的元素都是一个包含2个元素的字列表,并且需要将子列表里的2个元素相除,根据商来排序。
Python是否提供了简易的方法呢?
当然是有的,只需要使用下面这一行代码,就可以实现按单价从大到小排序。
s.sort(key=lambda x: x[1]/x[0], reverse=True)
sort()函数里的 key = lambda x : x[1]/x[0]
表示,这次的排序要指定关键字key。
这个关键字 key 的逻辑是什么呢?就是 lambda 函数。
在python里, lambda 函数也称为匿名函数,这种函数没有函数名,只有函数的内容,在上面的代码里,函数的内容就是 x : x[1]/x[0]
其中 x 就是循环列表s时,取出来的每一个子列表,当拿到一个x时,比如[3,223],就计算 x[1]/x[0] ,也就是总价值除以总重量,得到单价。
lambda 函数是Python一个重要的高级技巧,应用很广泛,但这里就不展开了。
按单价排好序之后的代码就很简单了,按单价依次去取就好了。
代码省略……
阿里巴巴的新挑战
阿里巴巴再一次溜进了山洞,这次,他发现山洞里摆满了各种各样的古董,每个古董上也贴了一张标签
关羽的青龙偃月刀 41公斤 100万
诸葛亮的白羽扇 1公斤 50万
射瞎夏侯惇的箭 0.1公斤 10万
汪伦送李白的酒杯 0.5公斤 20万
……

同样,假设小毛驴的承重是C公斤。
阿里巴巴应该怎么挑选,使得拿走古董的价值最大?
假设还是采用贪心策略,每次都拿单价最高的古董。
假设有下面4件古董,且小毛驴的承重是15公斤。
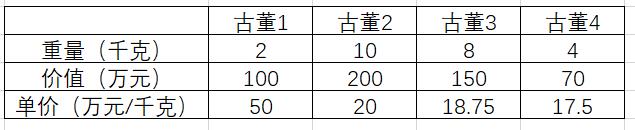
如果每次都挑选单价最高的古董
第1件,挑古董1。累积重量2公斤,累积价值100万
第2件,挑古董2。累积重量12公斤,累积价值300万。
第3件,挑古董3,累积重量已经超过小毛驴的承重,放不下了。
所以,阿里巴巴最多只能拿走价值300万的古董。
但是,很显然,阿里巴巴可以挑选古董1、古董3、古董4。总重量14公斤,总价值320万。
为什么贪心算法在这不适用了呢?
因为在这个问题里,局部最优不能得到全局最优。
怎么求解这个问题,已经超出了“贪心算法”的范畴。我们在后面再介绍。
像这类往口袋里装东西,在承重有限的情况下,怎么选择使得价值最大的问题,被称为“背包问题”。
“背包问题”是数学和计算机科学领域一个非常著名的研究方向。
“背包问题”根据假设条件的不同有多种典型的分类,比如上面的问题叫做“01背包问题”,后面我们将会介绍使用不同的算法解决各种类型的背包问题,包括如何解决“01背包问题”。

大家都知道,老板总是很忙,每天有很多会等着老板参加,但老板又没有时间参加所有的会议,所以需要秘书来合理安排。

某一天,老板对秘书说:“你安排一下,我希望今天尽可能多参加几场会议”。
秘书看了一下如下希望老板参加的会议,她应该如何安排,才能使老板参加会议的场次最多?
[[8,10],[9,11],[10,15],[11,14],[13,16],[14,17],[15,17],[17,18],[18,20],[16,19]]
列表里的每一个子列表都表示一场会议
比如第一场会议[8,10],表示这场会议开始时间是8点,结束时间是10点。
这个问题适合用贪心算法来做吗?
我们来分析一下:
1.全局的问题是否可以分解成多步
会议总是要一场一场开,所以全局问题可以分解成多步。
2.每一步是否可以做出“当前最好”的选择
每一步“当前最好”的选择是什么?
是会议时间最短?
是会议开始时间最早?
是会议结束时间最早?
如果一下子想不到的话,不妨用时间轴把会议表示出来。
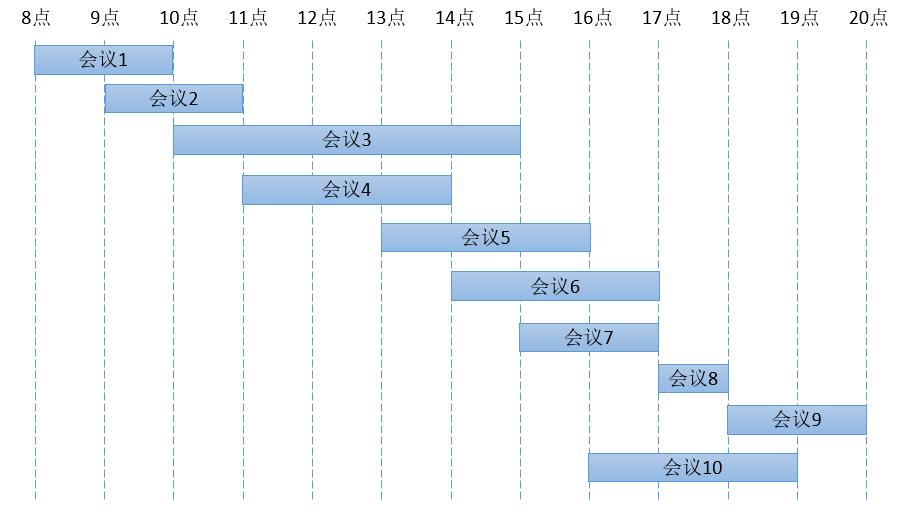
通过上面的图,就不难发现,每一步的“最优选择”应该是“结束时间最早,且和之前选择的会议时间不冲突”
3.每一步做出“当前最好”选择之后,是否全局的选择也是最优的。
不严格证明了。
如下是参考代码,不是性能最优的,但是是比较容易理解的。
第1步:对列表按会议结束时间排序 k.sort(key = lambda x:x[1])
第2步:把第一个会议直接加入到结果列表中。
第3步:双重循环,每次子循环都从剩余会议中挑出“结束时间最早,且和之前选择的会议时间不冲突的会议。”
k = [[8,10],[9,11],[10,15],[11,14],[13,16],[14,17],[15,17],[17,18],[18,20],[16,19]]
k.sort(key=lambda x:x[1])
result = []
result.append(k.pop(0))
while len(k) > 0:
pos = -1
minV = k[-1][1] + 1
for i in range(len(k)):
if k[i][0] < result[-1][1]:
continue
elif k[i][1] < minV:
pos = i
minV = k[i][0]
if pos > -1:
result.append(k.pop(pos))
else:
break
股票买卖时机问题

如果问沉迷炒股的人,最希望获得什么超能力。
答案一定是:预知未来的能力。
假设你拥有了预知未来的能力,来看下面2道题。
题目1:
给定一个列表,如[7,1,5,3,6,4]。表示的是某只股票每天的价格。
如果只允许你买卖一次,什么时候买入,什么时候卖出才能收益最大。
题目2:
还是某只股票,如[7,1,5,3,6,4]。
如果允许你买卖多次,什么时候买入,什么时候卖出才能收益最大。
扫描二维码
获取更多精彩
少儿编程
以上是关于46.贪心算法之二:做个好秘书,会议安排问题的主要内容,如果未能解决你的问题,请参考以下文章