48.贪心算法之四:跳跃游戏问题
Posted 和孩子一起学Python
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了48.贪心算法之四:跳跃游戏问题相关的知识,希望对你有一定的参考价值。
贪心算法的经典问题:跳跃游戏问题。
“大富翁”是一款非常经典的跳跃游戏。
在算法领域里,跳跃问题也是经典的算法问题。这一篇,我们要介绍的是其中2个可以用贪心算法解决的简单问题。

。
如下图
每一个格子上都有一个数字,表示你从这个格子上可以跳跃的最大长度。
如下图:
如果你站在第1个格子上,格子上的数字是3。
表示你可以跳1格,达到第2个格子
也可以跳2格,达到第3个格子
也可以跳3格,到达第4个格子。
但是你不能一次跳4格及以上

如果格子里的数字都是非负的整数。
问题1: 判断是否可以达到终点?
问题2:达到终点最少的跳跃次数是多少次?
仔细观察图中的数字,很容易找到如下的跳法是可以达到终点的。
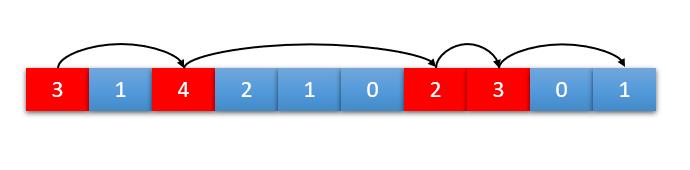
但如果我们将第3个位置上的数字4改成3,则走不到终点。
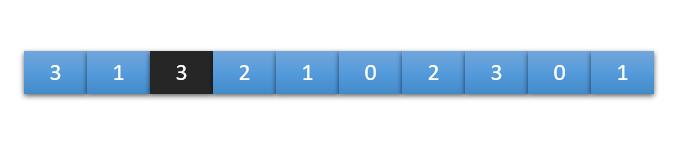
为什么呢?
根据题目的描述,格子上的数字表示从这个格子开始向前最远的跳跃范围。
我们给每个格子编上号,则有,
任一格子能够达到最远的距离 = 格子编号+格子上的数字。
比如编号0上的数字是3,从它开始,最远能达到的编号是 0+3 = 3
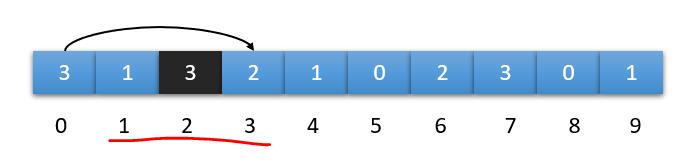
编号1上的数字是1,从它开始,最远能达到的编号是 1+1 = 2
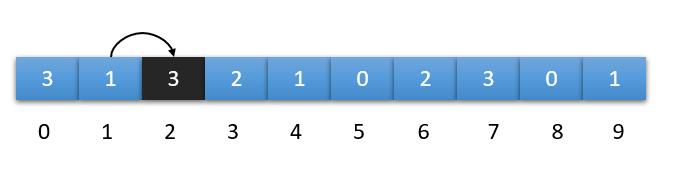
依次类推,我们发现一直走到编号5的格子。
它上面的数字是0,它能达到的最远编号是 5+0 = 5,
而它之前所有的格子,最远能达到的编号也是5。
也就是说,当试图走到编号6的位置时,却发现前面所有位置能达到的最远编号都小于6。所以,永远无法跳到编号是6的位置。
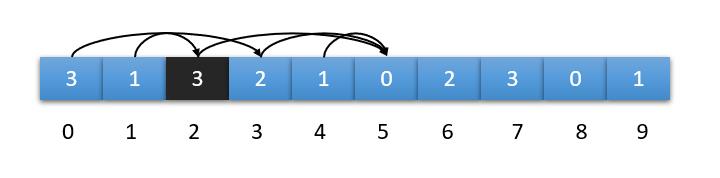
理解了上面的内容,程序就简单了。
我们只需要循环列表,一边循环,一边计算最远编号,只要不出现当前编号之前的能够达到的最远编号<当前编号,就可以一直走下去。
def jump(nums):
n = len(nums)
maxPos = 0
for i in range(n):
maxPos = max(nums[i]+i,maxPos)
if maxPos >= n-1 :
return True
elif i >= maxPos:
return False
else:
continue
假设给定的数字是一定可以达到终点的。
最少跳跃次数的思路很简单。
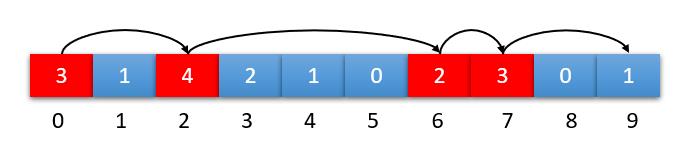
比如上面的跳跃方式,从编号0出发,0+3= 3,为什么会选择跳到编号2,而不是编号3?
如下图,为什么会从1,4,2里选择4,而不是其它2个呢?
我们计算一下每个位置能够达到的最远编号
编号1:1+1 = 2
编号2:2+4 = 6
编号3:3+2 = 5
所以,当然应该选择跳的最远的。
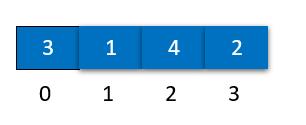
所以,我们在选择落脚位置时,需要比较这几个可能的落脚位置,谁能够达到的位置最远,就选择谁逻辑。
程序如下:
def jump(nums):
n = len(nums)
maxPos, end, step = 0, 0, 0
for i in range(n - 1):
if maxPos >= i:
maxPos = max(maxPos, i + nums[i])
if i == end:
end = maxPos
step += 1
return step
在花园和草地上,需要安装喷水装置给花草浇水

假设有一排名贵的花。为了给它们浇水,每盆花之间都安装了一个喷水龙头。
如下图,有4盆花,就有5个喷水龙头。
如果有n盆花,就有n+1个喷水龙头。
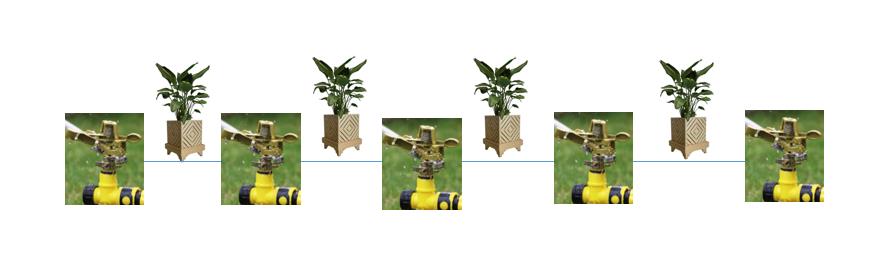
这些龙头用久了之后,能够喷水的范围变得乱七八糟,有的喷得远,有的喷得近,有的甚至坏掉了。
园丁用一组数字记录了每个龙头的喷水距离。
比如上图中5个龙头的喷水距离记录为
[2,3,0,0,1]
那么以第1个喷头为例,它的喷水范围是[-2,2],也就是说,它可以浇灌到前2盆花。
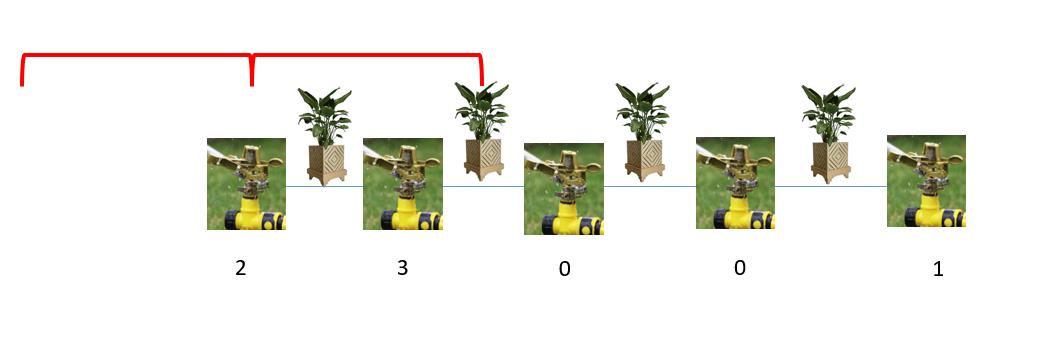
问题是:最少开多少个喷头,可以浇到所有的花。
扫描二维码
获取更多精彩
少儿编程
以上是关于48.贪心算法之四:跳跃游戏问题的主要内容,如果未能解决你的问题,请参考以下文章