数据结构与算法——图
Posted 胖虎不会写代码
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法——图相关的知识,希望对你有一定的参考价值。
最近在学数据结构,整理了一些资料,在这里以文章的形式发布出来,更新时间取决于我的学习进度。
图的定义
在计算机科学中,图是表达节点之间连接关系的数据结构,类似生活中的地图。图是由一系列顶点和若干连结顶点集合内两个顶点的边组成的数据结构。数学意义上的图,指的是由一系列点与边构成的集合,这里我们只考虑有限集。通常我们用 表示一个图结构,其中 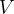 表示点集,
表示点集,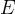 表示边集。
表示边集。
边分为有向和无向。类似于关注和好友的差别。A关注B不代表B关注A,那A到B就是有向的。而A是B的好友,那B也一定是A的好友,A和B的关系就是无向的。
严格地定义下图:图是由顶点集合(简称 点集)和顶点间的边(简称 边集)组成的数据结构,通常用 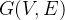 来表示。其中点集用
来表示。其中点集用 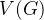 来表示,边集用
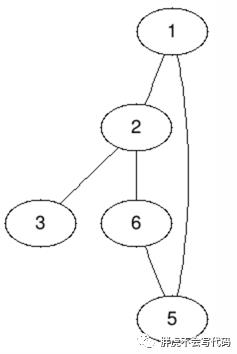
来表示,边集用 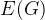 来表示。在无向图中,边连接的两个顶点是无序的,这些边被称为无向边。例如下面这个无向图
来表示。在无向图中,边连接的两个顶点是无序的,这些边被称为无向边。例如下面这个无向图 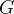 ,其点集
,其点集 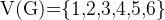 ,边集为
,边集为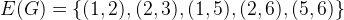 。
。
而在有向图中,边连接的两个顶点之间是有序的。例如下面这张有向图 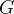 :
:
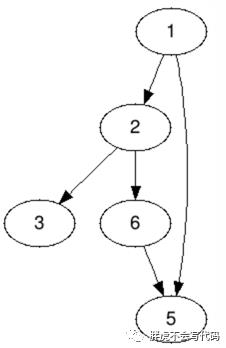
其点集 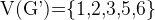 ,边集为
,边集为 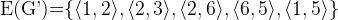 ,对于每条边
,对于每条边 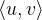 ,我们称其为从
,我们称其为从 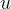 到
到 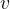 的一条有向边,
的一条有向边, 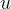 是这条有向边的起点,
是这条有向边的起点,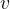 是这条有向边的终点。 注意在有向图中,
是这条有向边的终点。 注意在有向图中,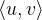 和
和 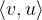 是不同的两条有向边。
是不同的两条有向边。
图的分类
有很少边或弧(如 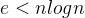 ,
, 指边数,
指边数,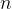 指顶点数)的图称为稀疏图,反之称为稠密图。如果图中边集为空,则称该图为零图。
指顶点数)的图称为稀疏图,反之称为稠密图。如果图中边集为空,则称该图为零图。
如果无向图中任何一对顶点之间都有一条边相连,也就是有 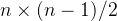 不重复的边,则这个无向图被称为完全图。类似地,如果有向图中任何一对顶点
不重复的边,则这个无向图被称为完全图。类似地,如果有向图中任何一对顶点 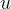 ,
,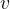 之间都有两条有向边
之间都有两条有向边 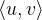 ,
,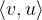 相连,则称这个有向图为有向完全图。下图就是由5个顶点组成的无向完全图。
相连,则称这个有向图为有向完全图。下图就是由5个顶点组成的无向完全图。
度
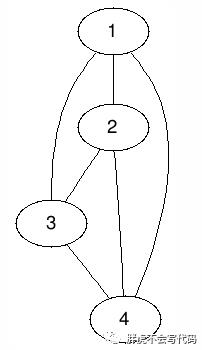
在无向图中,顶点的度是指某个顶点连出的边数。例如在下图中,顶点 b 的度数为 3,顶点 a 的度数为4。
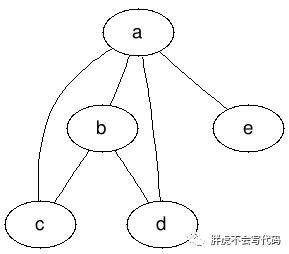
在有向图中,和度对应的是入度和出度这两个概念。顶点的入度是指以该顶点为终点的有向边数量;顶点的出度是指以顶点为起点的有向边数量。需要注意的是,在有向图里,顶点的度为入度与出度之和。例如在下图中,顶点 a 的入度为1 ,出度为3 ;顶点 c 的入度为2 ,出度为2。
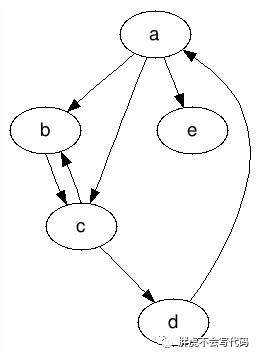
度的性质
在无向图或有向图中,顶点的度数总和为边数的两倍,即:
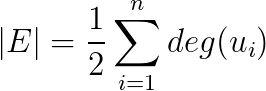
在无向图中,度序列的定义为:将图 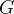 中所有顶点的度数排成一个序列 s ,则称 s 为图
中所有顶点的度数排成一个序列 s ,则称 s 为图  的度序列。例如下面这张图:
的度序列。例如下面这张图:
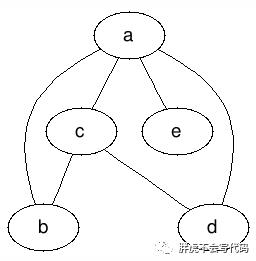
其对应的一个度序列为 4,2,3,2,1 ,而 1,2,2,3,4 也是其对应的度序列。换句话说,每个无向图对应的度序列不一定是唯一的。
一个序列是可图的,是指这个序列是某个无向图的度序列。判断一个序列是不是可图的,可以借助 Havel-Hakimi 定理:由非负整数组成的不递增序列: 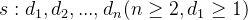 是可图的,当且仅当序列
是可图的,当且仅当序列
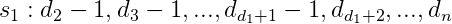
是可图的。序列 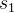 中有
中有 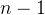 个非负整数,
个非负整数, 序列中
序列中 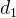 后的前
后的前 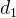 个度数(即
个度数(即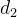 ~
~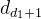 )减1后构成
)减1后构成 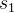 中的前
中的前 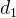 个数。
个数。
例如,我们要验证 4,3,2,2,1 是否是可图的,也就相当于判断 2,1,1,0 是否是可图的,也就相当于判断 0,0,0 是否是可图的。而 0,0,0 显然是可图的(对应一个零图)。因此,序列 4,3,2,2,1 就是可图的。
路径
在无向图 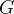 中,如果从顶点
中,如果从顶点 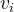 出发,沿着图中的边经过一些顶点
出发,沿着图中的边经过一些顶点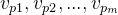 到达顶点
到达顶点 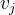 ,则称顶点序列
,则称顶点序列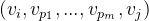 为从顶点
为从顶点 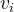 到顶点
到顶点 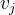 的一条路径(Path),其中
的一条路径(Path),其中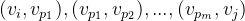 均为
均为 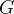 的边,如果
的边,如果 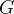 是有向图,则
是有向图,则 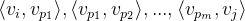 均为
均为 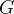 中的有向边。
中的有向边。
路径中边的数量被称为 路径长度。如果路径中的顶点均不重复,则称这条路径为 简单路径。如果路径中的第一个顶点 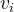 和走后一个顶点
和走后一个顶点 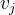 是同一个顶点,则称这条路径为回路。
是同一个顶点,则称这条路径为回路。
子图
对于两个图 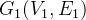 和
和 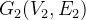 ,如果
,如果 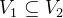 且
且 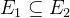 ,则称图
,则称图 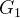 是图
是图 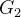 的子图。
的子图。
连通性
在无向图中,如果从顶点 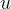 到顶点
到顶点 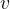 有路径,则称点
有路径,则称点 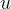 和点
和点 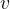 是连通的。如果无向图中任意一对顶点之间都是连通的,那么这个无向图就是连通图。如果一个无向图
是连通的。如果无向图中任意一对顶点之间都是连通的,那么这个无向图就是连通图。如果一个无向图 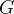 的子图是连通图,则称该子图为图
的子图是连通图,则称该子图为图 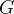 的连通子图。如果一个连通子图加上任何一个不在子图中的顶点后都无法构成连通子图,则称其为极大连通子图,又名连通分量。
的连通子图。如果一个连通子图加上任何一个不在子图中的顶点后都无法构成连通子图,则称其为极大连通子图,又名连通分量。
在有向图中,如果每对顶点之间都互相有路径可达,则称此图为强连通图。如果一个无向图 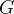 的子图是强连通图,则称该子图为图
的子图是强连通图,则称该子图为图 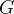 的强连通子图。如果一个强连通子图加上任何一个不在子图中的顶点后都无法构成强连通子图,则称其为极大强连通子图,又名强连通分量。
的强连通子图。如果一个强连通子图加上任何一个不在子图中的顶点后都无法构成强连通子图,则称其为极大强连通子图,又名强连通分量。
生成树
对一个无向图 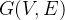 来说,它的一个生成树指的是包含
来说,它的一个生成树指的是包含 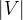 个顶点V-1条边的强连通子图。对于下面这个图
个顶点V-1条边的强连通子图。对于下面这个图 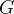 来说:
来说:
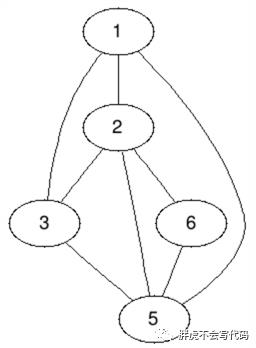
下面就是图 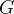 的一个生成树
的一个生成树
好了,对图的介绍就到这里,下篇文章会讲下图的一些基础算法。
再次比心~
以上是关于数据结构与算法——图的主要内容,如果未能解决你的问题,请参考以下文章