看图轻松理解数据结构与算法系列(二叉搜索树)
Posted 远洋号
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了看图轻松理解数据结构与算法系列(二叉搜索树)相关的知识,希望对你有一定的参考价值。
前言
推出一个新系列,《看图轻松理解数据结构和算法》,主要使用图片来描述常见的数据结构和算法,轻松阅读并理解掌握。本系列包括各种堆、各种队列、各种列表、各种树、各种图、各种排序等等几十篇的样子。
关于树
对于树的数据结构大家都了解,只是树的类型有很多,所以可能又会对树产生一种陌生感。树其实就是由有限n(n>=1)个节点组成的一个具有层次关系的集合,它看起来像一棵倒挂的树,所以称之为“树”。
树的特点
每个节点有若干个或0个子节点;
根节点没有父节点;
每一个非根节点有且只有一个父节点;
每个子节点可以分为多个不相交的子树;
二叉搜索树
二叉搜索树(Binary Search Tree,简写BST),又称为二叉排序树,属于树的一种,通过二叉树将数据组织起来,树的每个节点都包含了健值 key、数据值 data、左子节点指针、右子节点指针。其中健值 key 是最核心的部分,它的值决定了树的组织形状;数据值 data 是该节点对应的数据,有些场景可以忽略,举个例子,key 为身份证号而 data 为人名,通过身份证号找人名;左子节点指针指向左子节点;右子节点指针指向右子节点。
二叉搜索树特点
左右子树也分别是二叉搜索树。
左子树的所有节点 key 值都小于它的根节点的 key 值。
右子树的所有节点 key 值都大于他的根节点的 key 值。
二叉搜索树可以为一棵空树。
一般来说,树中的每个节点的 key 值都不相等,但根据需要也可以将相同的 key 值插入树中。
插入操作
如果为空树则将插入节点作为根节点。
如果不为空树则从根节点开始,比较插入节点与根节点的 key 值,值相同则不做任何处理直接返回,大于则继续比较右子节点R,小于则继续比较左子节点L。
右子节点R与插入节点比较,插入节点的 key 值大的话则继续往R节点的右子节点比较,小于的话则继续往R节点左子节点比较。
以此类推不断往下寻找,直到找到左子节点指针或右子节点指针为空的节点,将插入节点放进去。
对于下面这棵树,插入D和H,
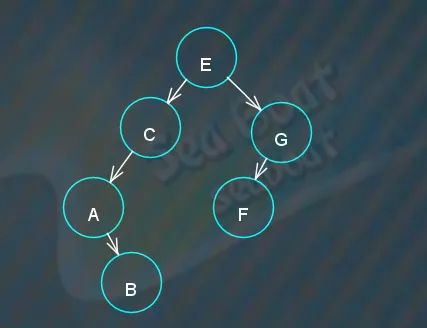
创建D节点并与根节点比较,
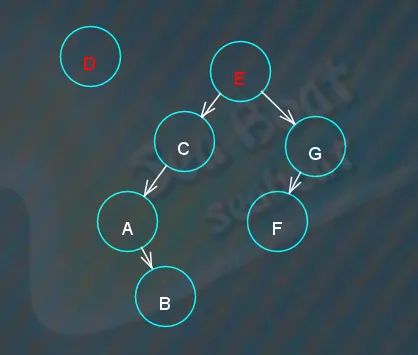
D 小于 E,于是往左子节点继续比较,
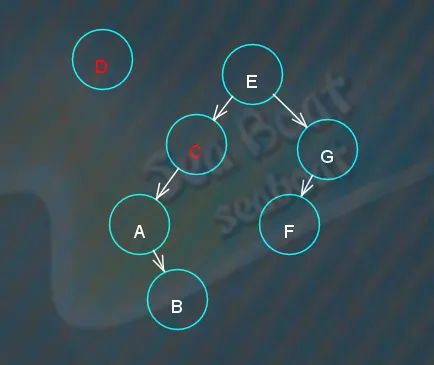
D 大于 C,应该往右子节点方向,而此时 C 节点的右子节点指针为空,D 节点可以放置进去。
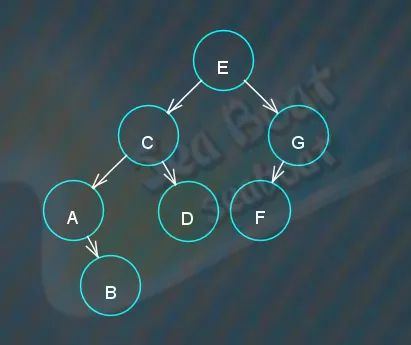
同样的,对于 H 节点,先创建 H 节点并与根节点比较,
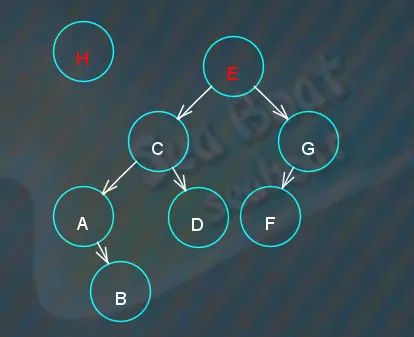
H 大于 E,于是往右子节点继续比较,
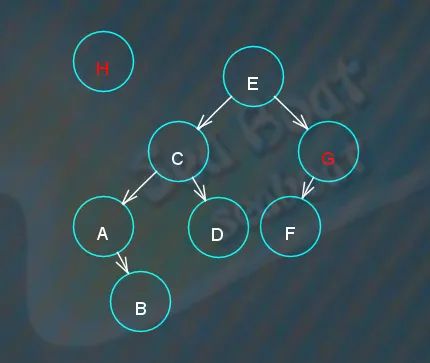
H 大于 G,应该往右子节点方向,而此时 G 节点的右子节点指针为空,H 节点可以放置进去。
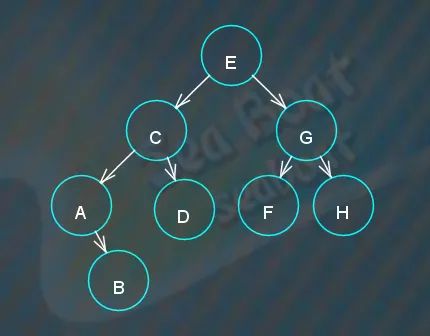
插入顺序性
二叉搜索树的形状与节点插入顺序不同而可能不同,比如对于A B C D E F G H这些节点集,按E C A B D G F H顺序插入则为,

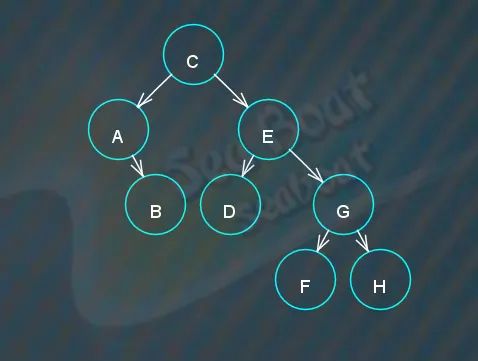
而如果调换前面两个节点,按照C E A B D G F H顺序插入则如下图,形状差别还是挺大的,
极端情况下,按照A B C D E F G H顺序插入,则为,

查询操作
则从根节点开始,比较查询节点与根节点的 key 值,值相同则表示找到该节点,直接返回,大于则继续往右子节点R查找,小于则继续往左子节点L查找。
右子节点R与查询节点比较,查询节点的 key 值大的话则继续往R节点的右子节点查找,小于的话则继续往R节点左子节点查找。
以此类推不断往下寻找,直到找到节点的 key 值与查询节点的相同,则表示查找成功,如果最终找不到则说明不存在该节点。
对于下图的树查找 key 值为“B”和“G”的节点,

“B”与根节点的 key 值比较,
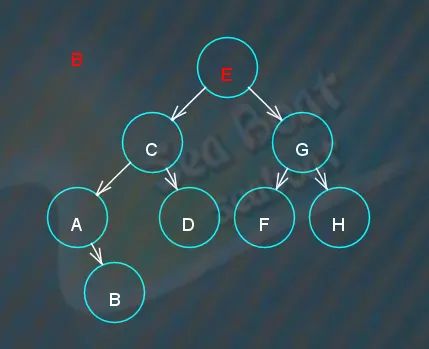
“B”小于“E”,往左子节点继续寻找,
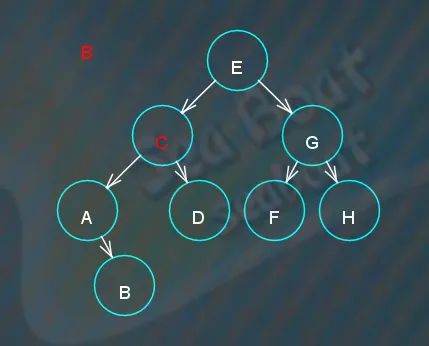
“B”小于“C”,往左子节点继续寻找,
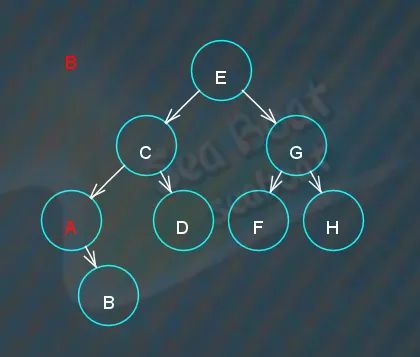
“B”大于“A”,往右子节点继续寻找,两者相等,找到。
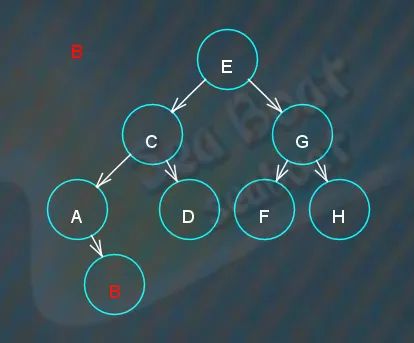
继续查询 key 值为“G”的节点,与根节点比较,
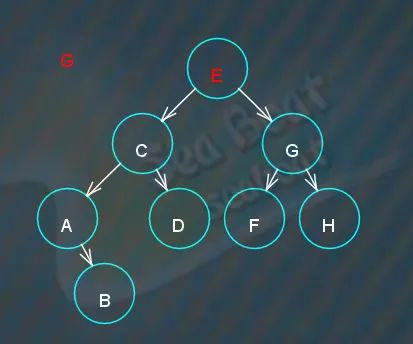
“G”大于“E”,往右子节点,两者相等,找到。
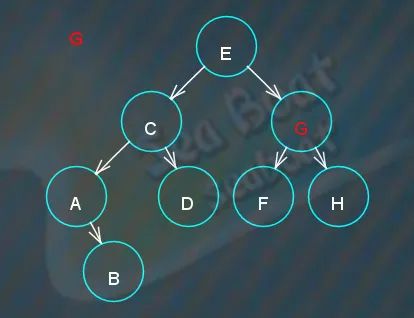
删除操作
删除操作分三种情况进行,
如果删除的节点为叶子节点,即它的左子节点指针和右子节点指针都为空时,则可以直接删掉该节点,并不会影响整棵树的结构。
如果删除的节点只有一个子节点(左子节点或右子节点),则直接将子节点提升到被删除的节点位置。
如果删除的节点有两个子节点,此时需要找到删除节点的中序后继或中序前驱来填补删除节点,中序后继其实就是所有大于删除节点中最小的那个,而中序前驱就是所有小于删除节点中最大的那个,因为二叉搜索树经过中序遍历后是一个递增序列,所以后继就是删除节点的后面那个节点,大于且大得最少的那个,比如
1 2 3 4 5中4就是3的后继。前驱就是删除节点前面那个节点,比如1 2 3 4 5中2就是3的前驱。
情况一
删除“B”叶子结点,从根节点开始查找,
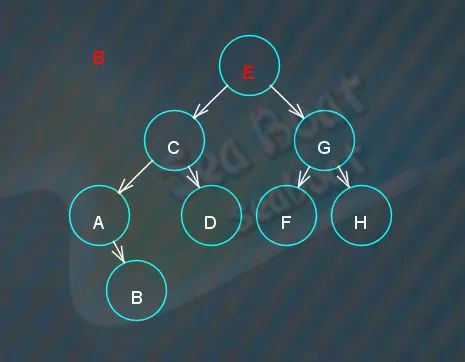
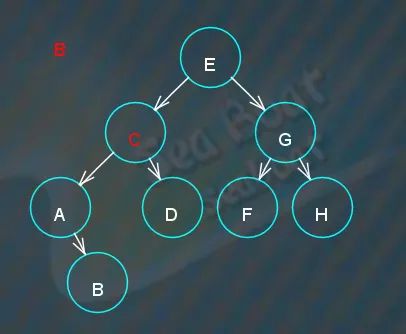
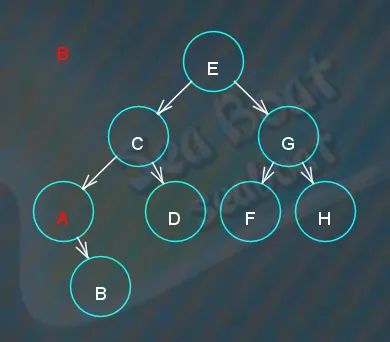
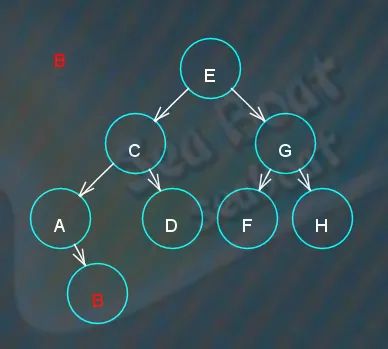
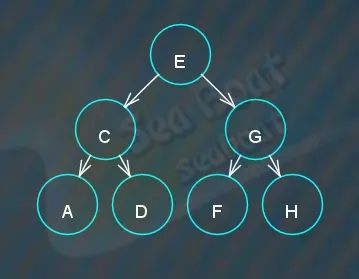
找到,直接删除,
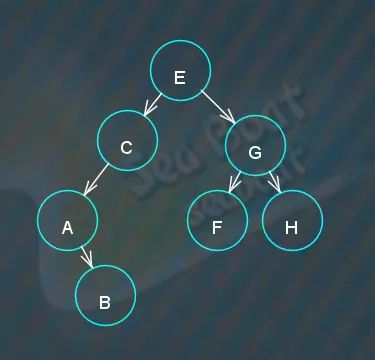
情况二
假如树的结构如下图,现在要删除“C”节点,
从根节点开始找,
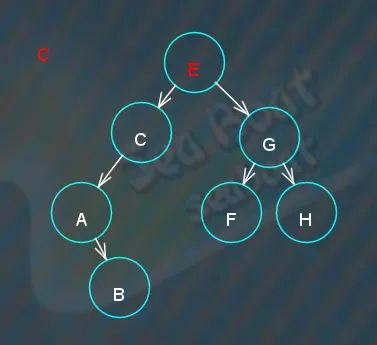
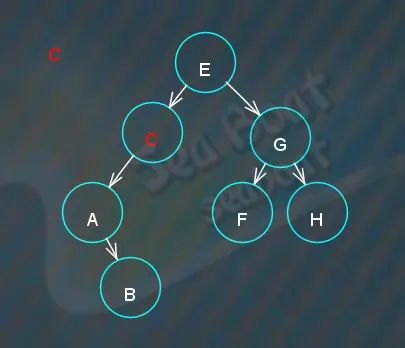
找到“C”节点,直接将原来指向“C”节点的右子节点指针指向“C”的子节点,
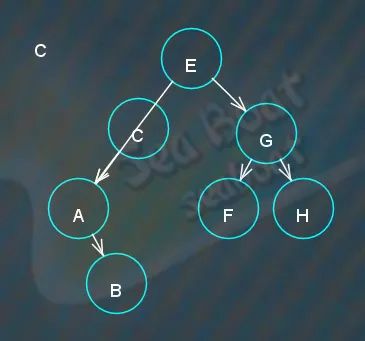
最终为,
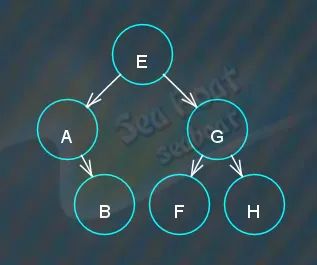
情况三
要在如下的树中删除“E”节点,
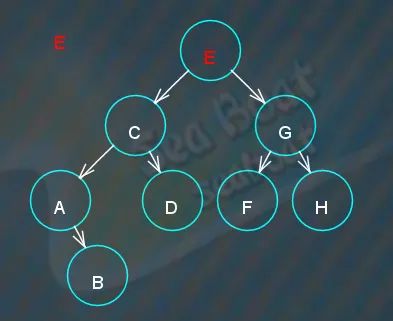
“E”节点存在两个子节点,于是开始寻找“E”节点的中序前驱来替换它,前驱在左子节点“C”下最大值的那个节点,
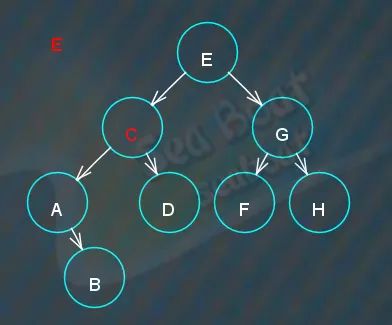
要找“C”节点下最大值节点则一直往右,
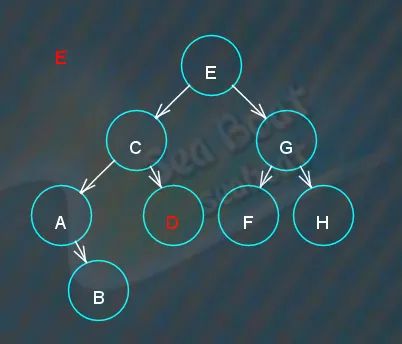
直到不能继续往下,即“D”节点即是前驱,用“D”节点来替换“E”节点,
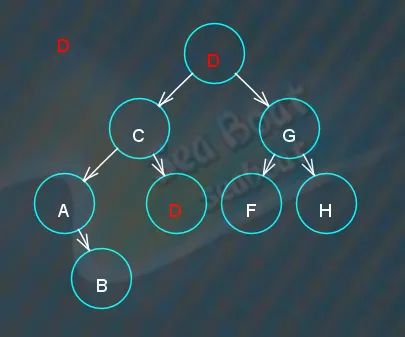
最终实现将“E”节点删除。
--------------------------------------
跟我交流:
-------------推荐阅读------------
以上是关于看图轻松理解数据结构与算法系列(二叉搜索树)的主要内容,如果未能解决你的问题,请参考以下文章