数据挖掘常用聚类分类模型速写贝叶斯分类

Posted 2021-04-25 从0开始学习数据挖掘

前面一节我们介绍了决策树分类器 (decision tree classifier)，举的例子是无脊椎动物的分类问题。我们选取包括体温、表皮覆盖类型、是否胎生等的多个属性，来确定这些动物的类别，包括哺乳类、爬行类、鸟类等。在这个例子中我们没有去讨论是否有两种动物它们在这些属性中取值完全相同，但是却归为不同的类别。现实生活中对于更复杂的分类问题，这种情况常常发生。比如很多疾病的发生原因至今尚不明确，通常我们会认为良好的饮食习惯是否健康，作息是否规律，人的心理性格和外界环境等会影响一个人的健康状况，但是无法通过这些因素完全预测一个人是否生病，会得什么病。一方面我们很难量化诸如人的心理、外界环境等来确定属性，甚至什么样的作息是最有益于健康的很多情况下也因人而异；另一方面，也有一些隐藏的属性可能未被我们发现。在这样的情况下就很容易发生，例如两个人在饮食习惯、作息、心理、性格、环境等各方面都非常相似但是一个生病一个未生病。现实生活中充满了不确定性，所以我们需要通过概率来将这种不确定因素引入我们的模型中，才能更好的进行分析预测。

（以下内容来源于数据挖掘经典书籍《数据挖掘导论》（《Introduction to Data Mining》）[美]作者Pang-Ning Tan，Michael Steinbach，Vipin Kumar 合著。）

    我们首先引入书中的一个例子，预测一个人是否拖欠贷款（default有违约的意思），见下图。属性包括是否有房（home owner）、婚姻状况（marital status）、年收入（annual income）。其中是否有房是二元属性（binary）；婚姻状况有单身（single）、已婚（Married）和离异（divorced）三种所以是分类变量（categorical）；年收入是具体数字，是连续变量。类别标签是二元的：是否拖欠贷款。

图：预测贷款拖欠问题的训练集

    通过这三种属性，我们不能确定的预测一个人是否会拖欠贷款，所以我们想知道，给定这些属性的值，其有多大概率拖欠贷款（或不拖欠贷款）。我们用X来表示属性，Y来表示分类，这个概率就可以表示为P(Y/X)。属性X有大量不同的组合，因此这个概率（被叫做后验概率posterior probability）不太好求出，贝叶斯定理（Bayes Theorem）让我们可以通过类条件（class-conditional）概率P(X/Y)，P(Y)（称为Y的先验概率prior probability）和P(X)来求出P(Y/X)，公式如下。

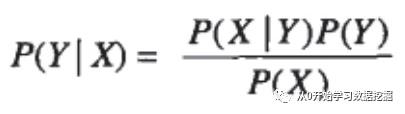
公式右边三个概率计算量要比直接求后验概率计算量小。

    实际的X包含多个属性，Y包含多个分类。如果我们假定属性之间相互独立，得到的就是朴素贝叶斯分类模型（Naive Bayes），那么就可以通过概率相乘的方法计算条件概率P(X/Y)，如下式所示。

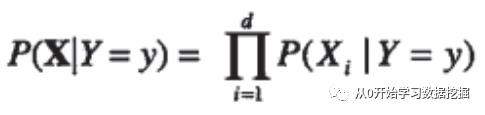
其中属性的个数为d。带入这个公式，贝叶斯定理就变成如下形式，

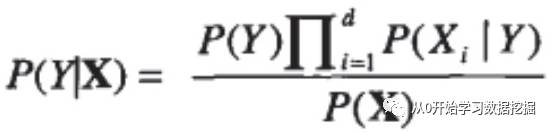
P(X)和P(Y)都比较容易求得，对条件概率P(Xi/Y)有分类属性和连续属性两种情况，对于分类属性可以直接求得，对于连续属性可以将其离散化，然后通过计数落入每个区间的样例的数量来计算概率。另外连续属性可以通过假设其满足某种概率分布来估计，比如通常假设变量服从高斯分布（就是含参数的那个e指数函数），然后通过训练数据估计高斯分布公式里的参数。高斯分布公式里的参数有总体均值μ和总体方差σ^2，这些可以通过抽样计算样本均值和样本方差来估计。这样就能确定高斯分布公式，其也就是概率密度函数（probability density function）。

    通过直接计数求解条件概率P(Xi/Y)会有个隐藏的问题，比如当训练集中的数据量较小，样例覆盖不全的情况下，有一些情况未被包含在训练集中，在这种情况下计算出来的概率P(Xi/Y)就为0，比如拖欠贷款的例子中，在Y=yes（拖欠贷款）类别中，X集为{无房，已婚，年收入=120K}的情况并未出现，如下所示，则概率为0。

概率为0，数学意义上就是这个情况绝对不可能发生，实际中这种情况可能发生，只是概率较小，或者并未包含在我们选取的训练集中。为了解决这个问题，我们将简单计数求概率的方法中加入一些参数，使得即使未被包含进训练集的情况求出的概率也不为0。公式的形式如下所示。

nc是计数，n是总数，简单计数求得的概率就是nc/n。新的概率估计公式是在分子分母中分别加入一项，其中m称为等价样本大小参数，p为用户指定参数。这种方法叫做m估计。

    朴素贝叶斯分类对噪声不敏感，对属性之间近似独立的情况下分类效果较好。但是属性之间独立这个条件太苛刻，现实中往往无法满足。贝叶斯信念网络（Bayesian belief networks， BBN）模型更加灵活，其不要求所有属性之间相互独立，而是允许指定哪些属性相互独立。

    贝叶斯网络模型，顾名思义是具有网状结构的模型，我们还可以想象类似如下图所示的有方向无环的结构，其节点之间有等级分别。

图：有向无环网络结构

    下图是一个发现心脏病（heart disease）和心口痛（heartburn）病人的贝叶斯网络结构的例子。图中我们可以看到例如饮食情况既有一定概率导致心脏病也有可能导致心口痛病，而心脏病和心口痛都有一定概率引起胸痛。在这个网络中，节点之间由一些列条件概率连结。

图：发现心脏病和心口痛病人的贝叶斯网络

    贝叶斯网络的具体实现算法在这里就不叙述了。贝叶斯网络模型的有效性取决于网络结构的选择，一旦确定了结构，各个节点间的概率就能通过与朴素贝叶斯方法中使用的类似的方法进行估计。构造网络结构的过程可能费时费力，但是一旦确定了结构，若要添加新的变量就很容易。