机器学习方法篇(15)------贝叶斯分类基础

Posted 2021-04-25 对半独白

➤ 导语

学过统计分析，一定知道什么是先验概率和后验概率，而贝叶斯分类的原理和这两种概率息息相关。为了更好地讲解贝叶斯分类，本节先讲讲概率统计相关的基础知识，方便之后的公式推导。

> > > >

概率基础

概率基础一共讲四个公式：加法公式、乘法公式/条件概率、贝叶斯公式、全概率公式。

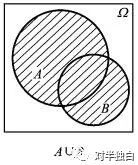
加法公式：P(A∪B) = P(A) + P(B) − P(A∩B) 。
上式对于任意两个事件A和B均成立。之所以要减掉A、B事件的并，是因为A发生时，B也有可能发生，即A与B不一定是条件独立事件。加法公式示意图如下： 

乘法公式/条件概率：

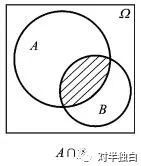
P(A∩B) = P(A)P(B|A) = P(B)P(A|B)。

所谓乘法，即在A事件发生的前提下P(A)，B事件也发生的概率P(B|A)；或者在B事件发生的前提下P(B)，A事件也发生的概率P(A|B)。乘法公式也叫作条件概率公式，示意图如下： 

贝叶斯公式：P(B|A) = P(B)P(A|B) / P(A)。
贝叶斯公式由乘法公式联立得出。

在机器学习中，贝叶斯公式通常写为P(h|D) = P(h)P(D|h) / P(D)。其中P(h)表示在没有进行样本训练之前假设h的初始概率，即前面提到的先验概率，先验概率反映了关于h的所有前提认知。而在机器学习中我们通常更关心后验概率P(h|D)，即给定D时h成立的概率。 

全概率公式：

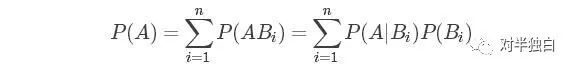
上式中，Bi表示两两不相容的时间，通俗的理解可以是两两不相同的时间段。P(A|Bi)表示在Bi时段A事件发生的概率，由于Bi两两不相容，因此上述P(A)的全概率公式使用加法公式计算得来。全概率公式图例描述如下： 

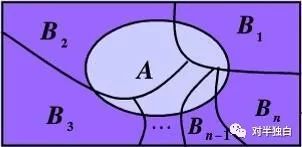
以上便是贝叶斯分类必备的四大概率公式，敬请期待下节内容。

结语

---

当前浏览器不支持播放音乐或语音，请在微信或其他浏览器中播放

每周一言

  音乐，是不二良药。