18贝叶斯分类器：朴素贝叶斯分类器(属性之间条件独立)

Posted 2021-04-25 FinTech修行僧

贝叶斯分类器：朴素贝叶斯分类器

预备知识

(1)P(A)：事件A发生的概率；P(B)：事件B发生的概率；

(2)联合概率：两个事件共同发生的概率，形式有

                P(AB)，P(A,B)，P(A∩B)

(3)先验概率(prior probability)

    根据以往经验和分析得到的概率；

(4)后验概率(posterior probability)，即条件概率

    在事件B发生下事件A的条件概率P(A|B)，读作“在B条件下A的概率”；

(5)贝叶斯定理

    

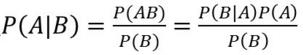
贝叶斯决策论(Bayesian decision theory)

贝叶斯决策论是概率框架下实施决策的基本方法。对分类任务来说，在所有相关概率都已知的理想情形下，贝叶斯决策论考虑如何基于这些概率和误判损失 来选择最优的类别标记。

假设

假设一个样本有N种可能的类别标记，即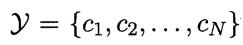，将一个真实标记为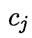的样本误分类为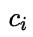所产生的损失记作。

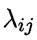基于后验概率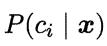 可获得将样本 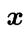分类为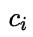 所产生的期望损失，即在样本 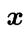上的“条件风险”：

        

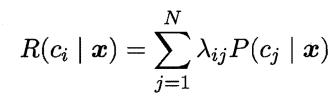
任务

我们的任务是寻找一个判定准则 以最小化总体风险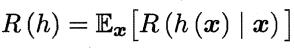

显然对每一个样本，若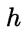能最小化条件风险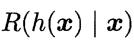，则总体风险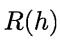也将被最小化。

贝叶斯判定准则(Bayes decision rule)

为最小化总体风险，只需在每个样本上选择那个能使条件风险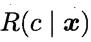最小的类别标记，即：

                    

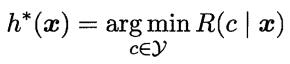
其中：

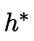          是贝叶斯最优分类器；

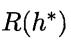          是贝叶斯风险；

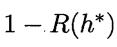         反映了分类器所能达到的最好性能(精度)；

具体来说

若目标是最小化分类错误率，则有

        误判损失：

        条件风险：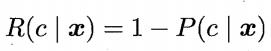

        最小化分类错误率的贝叶斯最优分类器：

        

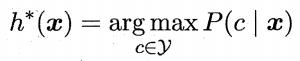
即对每个样本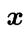，选择能使后验概率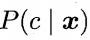最大的类别标记。

那么如何估计后验概率P(c|x)呢？

有两种方法：

(1)判别式模型：给定 x ，直接建模P(c|x)，来预测 c ，如决策树，BP神经网络，支持向量机；

(2)生成式模型：对联合概率分布P(x , c)建模，然后由此获得P(c|x)

对生成式模型来说，必然得考虑：

                        

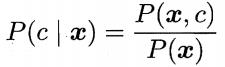
再基于贝叶斯定理，有

                        

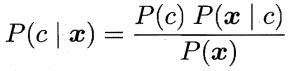
其中：

     1)  P(c)是类先验概率；

     2)  P(x|c)是样本x相对于类标记c的，类条件概率 ，或称似然；

     3)  P(x)是用于归一化的证据因子；

对给定的样本 x ，证据因子P(x)与类标记无关，因此估计P(c|x)的问题就就转化为如何基于训练数据D来估计先验概率P(c)和似然P(x|c) 。

实际上，P(c)是训练集中各类样本出现的概率，P(x|c)是在训练集中，在类别C里特征 x 出现的条件概率 ，P(x)是训练集中特征x出现的概率；

极大似然估计与贝叶斯估计

极大似然估计(极大似然法)

估计类条件概率的常用策略

假定类条件概率具有某种确定的概率分布形式，再基于训练样本对概率分布的参数进行估计。

具体地，记关于类别C的类条件概率为P(x|c)，假设P(x|c)具有确定的形式并且被参数向量θ_c唯一确定，则我们的任务就是利用训练集D估计参数θ_c。为明确起见，我们将P(x|c)记为P(x|θ_c) 。

令D_c表示训练集D中第c类样本组成的集合，假设这些样本是独立同分布的，则参数θ_c对于数据集D_c的似然是

                

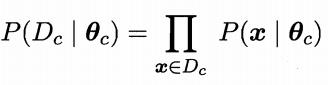
对θ_c进行极大似然估计，就是去寻找能最大化似然函数P(D_c|θ_c)的参数值 。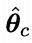

直观上看，极大似然估计是试图在θ_c所有可能的取值中，找到一个能使数据出现的“可能性”最大的值。

由于连乘操作易造成下溢，通常使用对数似然(log-likelihood)：

            

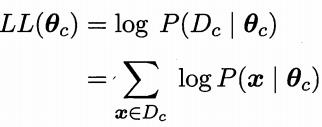
此时，参数θ_c的极大似然估计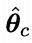为：

            

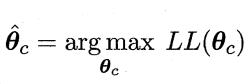
在连续属性情形下

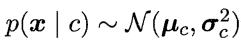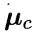假设概率密度函数，则参数和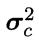的极大似然估计为：

            

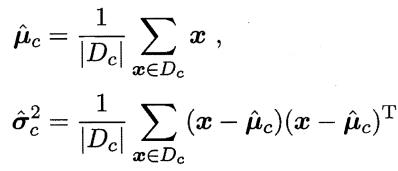
总结：这种参数化的方法，虽然能使条件概率估计变得相对简单，但估计结果的准确性严重依赖于所假设的概率分布形式是否符合潜在的真实数据分布。在现实任务中，往往还需要利用，关于应用任务本身的经验知识来假设概率分布形式。

贝叶斯估计

用极大似然估计可能会出现所要估计的概率值为0的情况，这时会影响到后验概率的计算结果，从而使分类产生偏差，解决这一问题的方法是采用贝叶斯估计。

具体地，条件概率的贝叶斯估计是

            

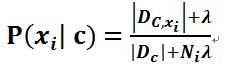
先验概率的贝叶斯估计是

            

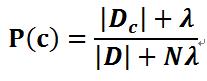
其中，N_i 表示第 i 个属性可能的取值数 ，D_c 表示训练集D中第 c 类样本组成的集合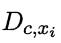，表示 D_c 中第 i 个属性上取值为 x 的样本组成的集合，N 表示训练集D中可能的类别数，λ≥0 。

因此，贝叶斯估计等价于在随机变量各个取值的频数上赋予一个正数 λ 。当 λ=0时，就是极大似然估计；当 λ=1时，就是拉普拉斯平滑(Laplace smoothing)，或叫 拉普拉斯修正。

拉普拉斯修正，避免了其他属性携带的信息被训练集中未出现的属性值“抹去”，即避免了因训练集样本不充分而导致概率估值为零的问题，并且在训练集变大时，修正过程所引入的先验的影响，也会逐渐变得可忽略，使得估值渐趋向于实际概率值。

朴素贝叶斯分类器

不难发现，基于贝叶斯公式

                

来估计后验概率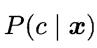的主要困难在于：

类条件概率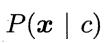是所有属性上的联合概率，难以从有限的训练样本直接估计而得，在计算上将会遭遇组合爆炸问题，在数据上将会遭遇样本稀疏问题，而且属性越多，问题越严重。因此，为了避开这些障碍，就有了朴素贝叶斯分类器。

朴素贝叶斯分类器采用“属性条件独立性假设”，对已知类别，假设所有属性相互独立。换言之，假设每个属性独立地对分类结果发生影响。

朴素贝叶斯分类器的表达式

基于属性条件独立性假设，后验概率公式为：

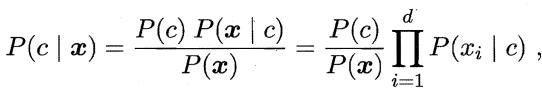
其中， d 为属性数目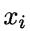， 为 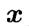在第 i 个属性上的取值。

由于对所有类别来说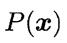，相同，因此贝叶斯判定准则有

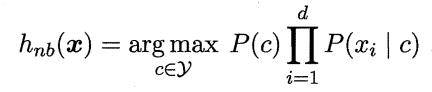
其中，

            

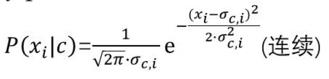
这就是朴素贝叶斯分类器的表达式。也就是说，根据期望风险最小化原则，便使后验概率最大化。

朴素贝叶斯分类器的分类流程

第一步，根据训练数据，计算先验概率和条件概率：

先验概率(即分别算出各个类出现的概率)

                        

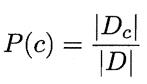
条件概率(即在已知类的情况下，分别求出各个特征出现的概率)：

                        

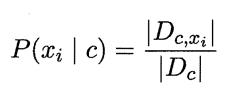
第二步，根据给定的实例 x，计算其后验概率(即根据属性，计算实例分别为各个类别时的概率)：

根据下式，分别计算实例为各个类别时的后验概率大小

                        

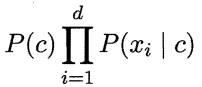
第三步，从后验概率中，选取概率最大的后验概率所对应的类，作为实例 x 的类别：

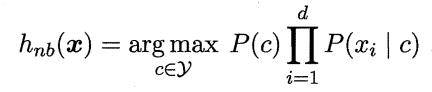
朴素贝叶斯分类器分类流程如下图所示：

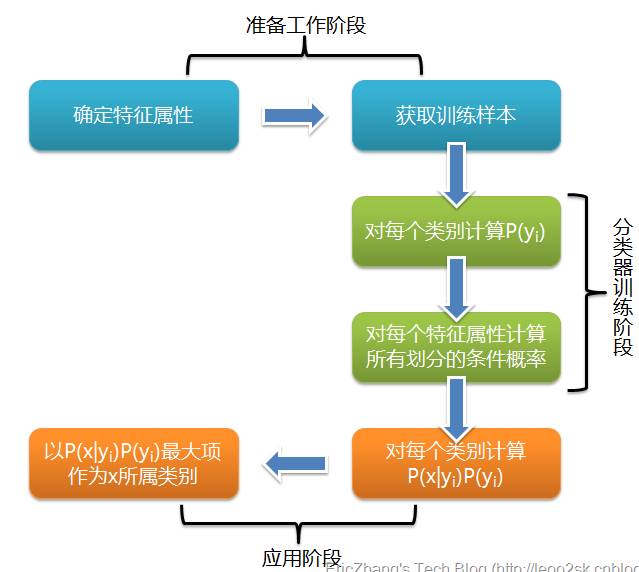
可以看到，整个朴素贝叶斯分类分为三个阶段：

第一阶段——准备工作阶段：

这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。

第二阶段——分类器训练阶段：

这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。

第三阶段——应用阶段。

这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。

朴素贝叶斯分类实例：检测SNS社区中不真实的账号

对于SNS社区来说，不真实账号（使用虚假身份或用户的小号）是一个普遍存在的问题，作为SNS社区的运营商，希望可以检测出这些不真实账号，从而在一些运营分析报告中避免这些账号的干扰，亦可以加强对SNS社区的了解与监管。

如果通过纯人工检测，需要耗费大量的人力，效率也十分低下，如能引入自动检测机制，必将大大提升工作效率。这个问题说白了，就是要将社区中所有账号在真实账号和不真实账号两个类别上进行分类，下面我们一步一步实现这个过程。

      

首先设C=0表示真实账号，C=1表示不真实账号。

(1)、确定特征属性及划分

      

这一步要找出可以帮助我们区分真实账号与不真实账号的特征属性，在实际应用中，特征属性的数量是很多的，划分也会比较细致，但这里为了简单起见，我们用少量的特征属性以及较粗的划分，并对数据做了修改。

      

我们选择三个特征属性：

a1：日志数量/注册天数，a2：好友数量/注册天数，a3：是否使用真实头像。在SNS社区中这三项都是可以直接从数据库里得到或计算出来的。

      

下面给出划分：

a1：{a<=0.05, 0.05<a<0.2, a>=0.2}；

a2：{a<=0.1, 0.1<a<0.8, a>=0.8}；

a3：{a=0（不是）,a=1（是）}；

(2)、获取训练样本

这里使用运维人员曾经人工检测过的1万个账号作为训练样本(具体数据省略，看懂问题解决思路即可)。

(3)、计算训练样本中每个类别的频率

 用训练样本中真实账号和不真实账号数量分别除以一万，得到：

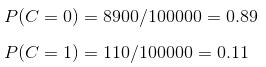
(4)计算每个类别条件下，各个特征属性划分的频率

    

(5)使用分类器进行鉴别

下面我们使用上面训练得到的分类器鉴别一个账号，这个账号使用非真实头像，日志数量与注册天数的比率为0.1，好友数与注册天数的比率为0.2。

可以看到，虽然这个用户没有使用真实头像，但是通过分类器的鉴别，更倾向于将此账号归入真实账号类别。这个例子也展示了当特征属性充分多时，朴素贝叶斯分类对个别属性的抗干扰性。

参考文献

【1】李航 · 统计学习方法 · 清华大学出版社

【2】周志华 · 机器学习 · 清华大学出版社

【3】贝叶斯分类器(一)：朴素贝叶斯分类器与半朴素贝叶斯分类器  http://blog.csdn.net/rongrongyaofeiqi/article/details/53100391

【4】算法杂货铺---分类算法之朴素贝叶斯分类 http://www.cnblogs.com/leoo2sk/archive/2010/09/17/naive-bayesian-classifier.html