从朴素贝叶斯分类到贝叶斯网络
Posted RM数据工作室
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了从朴素贝叶斯分类到贝叶斯网络相关的知识，希望对你有一定的参考价值。
机器学习专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。在学习过程中，绝大部分学习任务是分类，朴素贝叶斯分类是一种最简单且非常有效的分类算法。由朴素贝叶斯分类谈到图模型中的贝叶斯网络，贝叶斯网络模型最简单的例子也是“分类器”，即在观测节点输入多个特征，就能获得这些特征所对应的具体事物。
先验知识：
拉普拉斯平滑（贝叶斯网络中用到：防止0概率估计）：
比如一个例子，垃圾邮件分类：
P(x1|c1)：表在垃圾邮件c1这个类别中，单词x1出现的概率。x1是待考察的邮件中某个单词。
n1：c1这个类别中单词x1出现的次数，没有出现为0；
n1：c1这个类别中所有文档出现过的单词总数目。
N：所有文档数目，包括垃圾邮件和非垃圾邮件的单词的总数目
得到公式：
（为什么分母加N这样设计，在c1类别中，我们要计算所有词x1，x2，，，xN，所以加了N次1）
一．朴素贝叶斯分类
贝叶斯公式：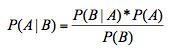
设x={a1,a2,a3,,,,,am}为一个待分类项，而每个a为x的一个特征属性（比如分鸡和大象，他们特征属性可以是：嘴巴，翅膀，脚，，，）
类别集合c={c1，c2，c3，，，，，，cn} （被分到的类别：c1可以是鸡，c2可以是桌子）
计算P(c1|x), P(c2|x), P(c3|x) ,,,,,P(cn|x) 每个类别在训练样本中出现的概率
P(ck|x)=max{P(c1|x), P(c2|x),,,,,P(cn|x)}
怎么得到第3步？
一个已经分类好的分类项集合，这个集合叫训练样本集。
在训练样本中：统计各个类别c1，c2，，，，cn 下，各个特征a1，a2，，，，an的概率。
P（a1|c1） P（a1|c2） P（a1|c3） P（a1|c4），，，， 在鸡，猪，椅子中 计算a1脚这个特征的概率。
P（a2|c1） P（a2|c2） P（a2|c3） P（a2|c4），，，， 在鸡，猪，椅子中 计算a2眼睛这个特征的概率。
3. 如果各个类别的特征独立的，则根据贝叶斯定理得：
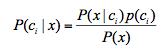（p（x）是常数，后验概率= 样本信息*先验概率）
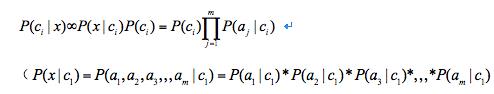特征独立）
例子：
有10000封邮件，每个邮件已被标记为垃圾邮件或非垃圾邮件。
如果有第10001封邮件，确定他是垃圾邮件还是非垃圾邮件？
现用朴素贝叶斯方法求解。
类别：c1：垃圾邮件，c2：非垃圾邮件
特征项的建立：
先将每封邮件（10001封）分词
统计所有邮件中的单词，总的单词个数（不重复的）为N
把每封邮件都映射成一个维度为N的向量X={w1,w2,w3,,,,wN}(若这个单词出现为1，不出现置0) （这里用的词袋模型，认为每个特征的权值一样，也可以用TF-IDF对不同的特征加权）
计算P(c1|x), P(c2|x)
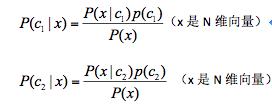
因为：
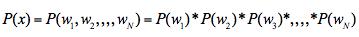
为常数（特征独立，P（wi）就是表示在所有样本中单词wi出现的概率）
所以：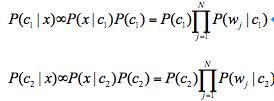
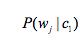表示：在所有垃圾邮件c1中，单词wj出现的概率
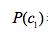表示：在所有10001封邮件中，垃圾邮件c1出现的概率（用频数代表概率：垃圾邮件个数/10001）
6.
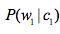：是计算在垃圾邮件中，单词w1出现的概率
如果用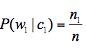
（n1：在所有垃圾邮件中w1出现的次数，没出现为0
n： 在所有垃圾邮件中单词的个数（可以是重复的））
那么，这个概率可能为0，怎么办？
用拉普拉斯平滑解决：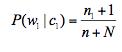
（N：所有单词的数目（不重复），防止出现0概率）
为什么分母加N，分子加1？因为（n1+1）+（n2+1）+（n3+1）+，，，（nN+1）= n+N
用拉普拉斯平滑处理P（wi），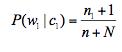
（ni表示在所有邮件中单词wi出现的次数，n表示所有邮件单词的总数（可以重复），N：所有单词的数目（不重复））
7. 
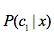和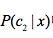
哪个概率大就是哪个类
二．贝叶斯网络
图模型：用图的方式表达概率推理，用图结构描述随机变量之间的依赖关系，节点表示随机变量，边表示随机变量之间的依赖关系。
有向图：贝叶斯网络
无向图：马尔科夫随机场
贝叶斯网络的定义
贝叶斯网络（Beyesian network）或有向无环图模型（directed acyclic graphic model），是一种概率图模型。它是一种模拟人类推理过程中因果关系的不确定性处理模型，其网络拓扑结构是一个有向无环图（DAG）。
把某个系统中涉及节点表示随机变量{x1，x2，x3，，，xn}，可以是可观测的变量、隐变量、未知参数等。认为有因果关系（或非条件独立）的变量或命题则用箭头来连接。若两个节点间以一个单箭头连接在一起，表示其中一个节点是“因(parents)”，另一个是“果(children)”，两节点就会产生一个条件概率值。
总而言之，连接两个节点的箭头代表此两个随机变量是具有因果关系，或非条件独立。
下面看一个简单的贝叶斯网络：
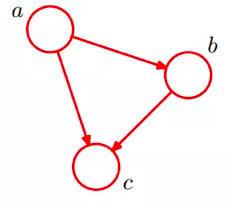
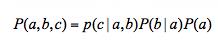
2. 通过贝叶斯网络判定条件独立的三种形式
下面给一个一般的贝叶斯网络：
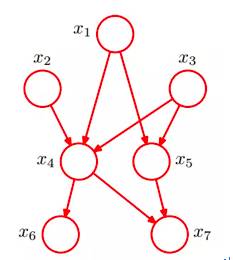
从图中可得：
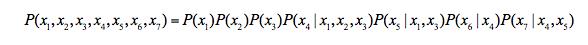
下面分别介绍，，三种形式
（1）tail-to-tail
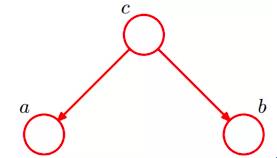
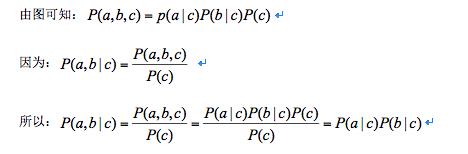
即：在c给定条件下（c已知），a和b独立。
在之前图中，当x4给定，x6和x7独立，对应tail-to-tail
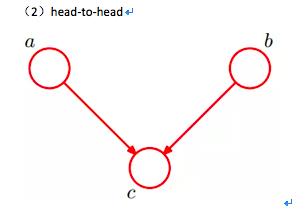
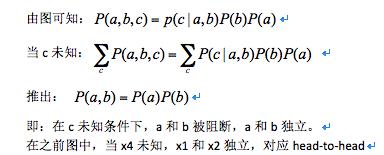
在之前图中，当x4未知，x1和x2独立，对应head-to-head
（3）head-to-tail
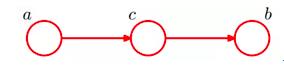
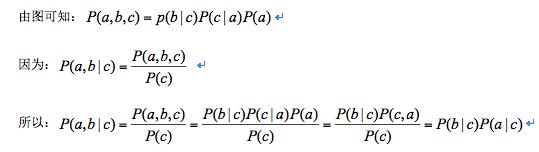
即：在c给定条件下（c已知），a和b独立。
由此我们引出马尔科夫链（Markov chain）:
根据之前对head-to-tail的讲解，我们已经知道，在xi给定的条件下，xi+1的分布和x1,x2…xi-1条件独立。即当前状态只跟上一状态有关，跟上上或上上之前的状态无关。这种顺次演变的随机过程，就叫做马尔科夫链（Markov chain）。
有：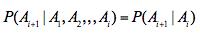
例子：假设有两个服务器（S1，S2），会传送数据包到用户端 (以U表示之)，但是第二个服务器的数据包传送成功率会与第一个服务器传送成功与否有关，因此此贝叶斯网络的结构图可以表示成如图2的型式。就每个数据包传送而言，只有两种可能值：T(成功) 或 F(失败)。
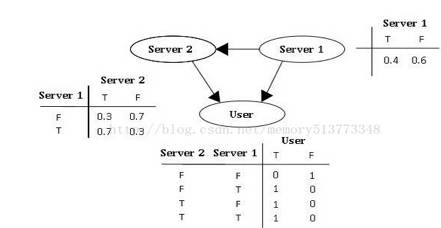
则此贝叶斯网络之联合概率分配可以表示成：
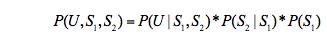
“假设已知用户端成功接受到数据包，求第一服务器成功发送数据包的概率?”
参考：
1.July 《从贝叶斯方法谈到贝叶斯网络》
2.邹博 机器学习视频
3. 贝叶斯网络http://www.mamicode.com/info-detail-319717.html
以上是关于从朴素贝叶斯分类到贝叶斯网络的主要内容，如果未能解决你的问题，请参考以下文章