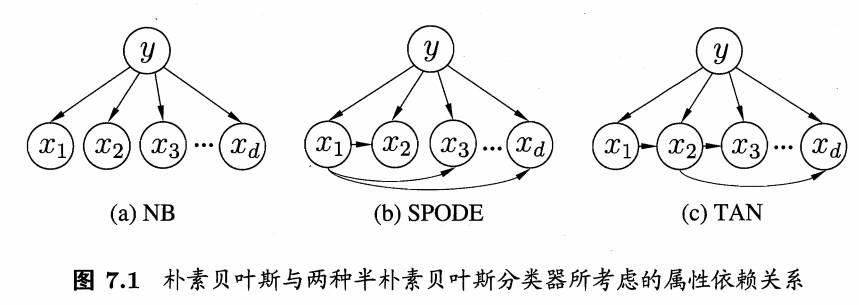
19贝叶斯分类器:半朴素贝叶斯分类器(属性之间存在依赖)
Posted FinTech修行僧
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了19贝叶斯分类器:半朴素贝叶斯分类器(属性之间存在依赖)相关的知识,希望对你有一定的参考价值。
贝叶斯分类器:半朴素贝叶斯分类器
半朴素贝叶斯分类器(属性之间不完全独立)
为了降低贝叶斯公式
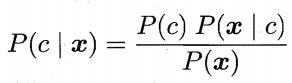
中估计后验概率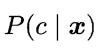 的困难,朴素贝叶斯分类器采用了属性条件独立性假设,但在现实任务中这个假设往往很难成立。于是,人们尝试对属性条件独立性假设进行一定程度的放松,由此产生了“半朴素贝叶斯分类器”(semi-naive Bayes classifiers) 。
的困难,朴素贝叶斯分类器采用了属性条件独立性假设,但在现实任务中这个假设往往很难成立。于是,人们尝试对属性条件独立性假设进行一定程度的放松,由此产生了“半朴素贝叶斯分类器”(semi-naive Bayes classifiers) 。
半朴素贝叶斯分类器的基本想法是适当考虑一部分属性间的相互依赖信息,从而既不需进行完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系,即属性间不完全独立。
“独依赖估计”(One-Dependent Estimator,简称ODE)是半朴素贝叶斯分类器最常用的一种策略。所谓“独依赖”,就是假设每个属性在类别之外最多仅依赖于一个其他属性,即
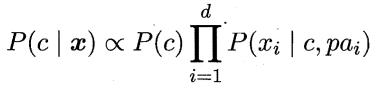
其中,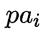 为属性
为属性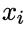 所依赖的属性,称为
所依赖的属性,称为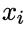 的父属性。
的父属性。
此时,对每个属性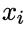 ,若其父属性
,若其父属性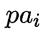 已知,便可根据训练数据估计出概率值
已知,便可根据训练数据估计出概率值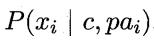 (注,这里是 已知c和pai 的条件下,得到xi 的概率) 。
(注,这里是 已知c和pai 的条件下,得到xi 的概率) 。
于是,问题的关键就转化为:如何确定每个属性的父属性,不同的做法会产生不同的独依赖分类器。
注意以下两个概率的区别:
P(xi | c,xj) :已知 c 和 xj 的条件下,xi 的概率;
P(xi,xj | c):已知 c的条件下,xi 和 xj 的联合概率;
也就是说,逗号运算符优先于条件运算符“ | ”,即逗号两边的操作数优先;

如何确定父属性呢?
有三种方法:
(1)SPODE方法(Super-Parent ODE)
即假设所有属性都依赖于同一个属性,这个属性称为“超父”,然后通过交叉验证等模型选择方法来确定超父属性。
(2)TAN(Tree Augmented naive Bayes)--树增强朴素贝叶斯方法
它是在最大带权生成树算法的基础上,通过如下步骤将属性间依赖关系约简为如下图所示的树形结构:
a、计算任意两个属性之间的条件互信息(conditional mutual information)
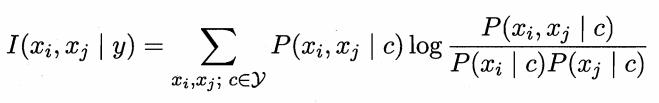
b、以属性为结点构建完全图,任意两个结点之间边的权重设为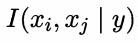 ;
;
c、构建此完全图的最大带权生成树,挑选根变量,将变置为有向;
d、加入类别结点 y ,增加从 y 到每个属性的有向边;
容易看出,条件互信息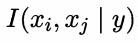 刻画了属性
刻画了属性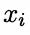 和
和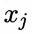 在已知类别情况下的相关性,因此,通过最大生成树算法,TAN实际上仅保留了强相关属性之间的依赖性。
在已知类别情况下的相关性,因此,通过最大生成树算法,TAN实际上仅保留了强相关属性之间的依赖性。
举个例子:
已知
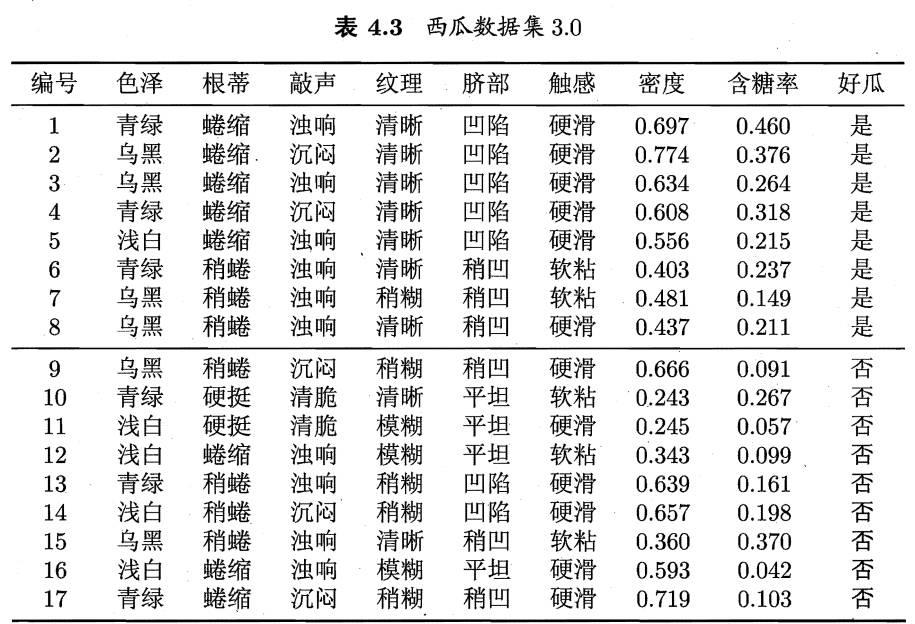
则依据TAN有
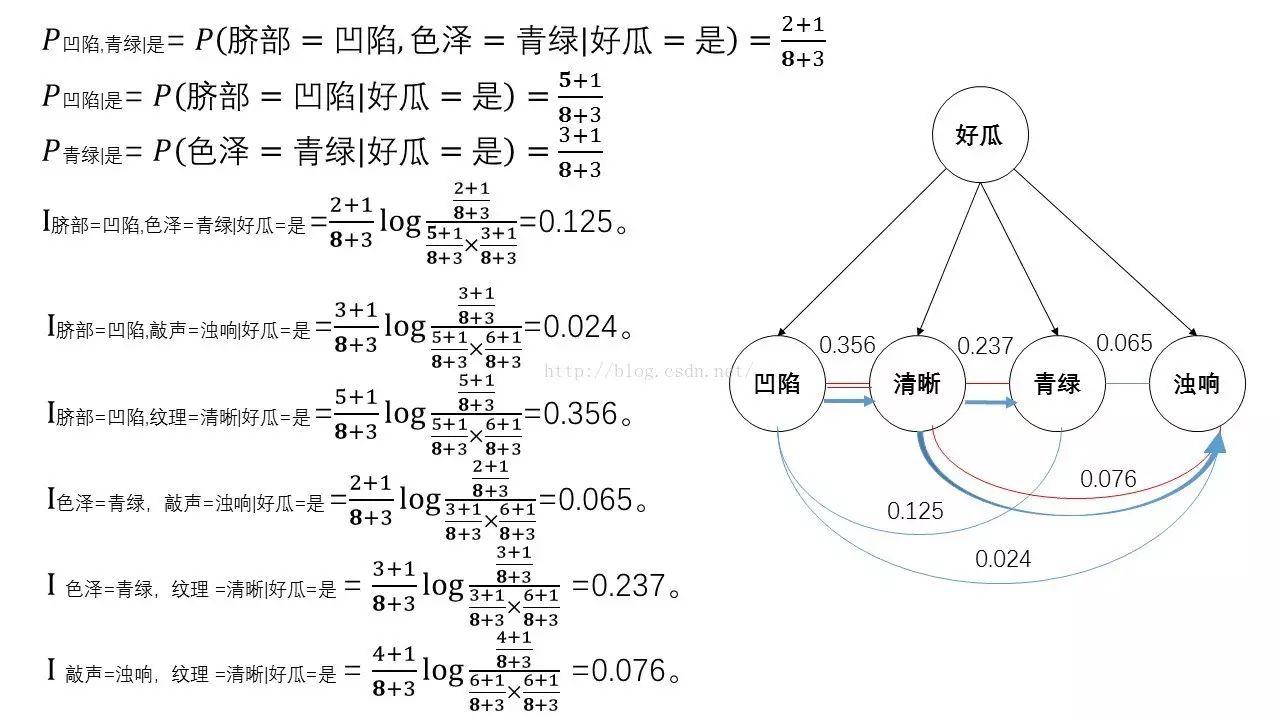
注:这里计算概率时用了拉普拉斯修正。
(3)AODE(Averaged One-Dependent Estimator)
它是一种基于集成学习机制、更为强大的独依赖分类器。
它尝试将每个属性作为超父来构建SPODE,然后将那些具有足够训练数据支撑的SPODE集成起来作为最终结果,即
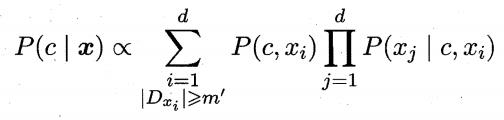
其中,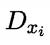 是在第
是在第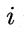 个属性上取值为
个属性上取值为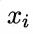 的样本集合,
的样本集合,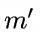 为阈值常数,默认设置为30。显然,AODE需估计
为阈值常数,默认设置为30。显然,AODE需估计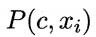 和
和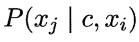 ,于是有:
,于是有:
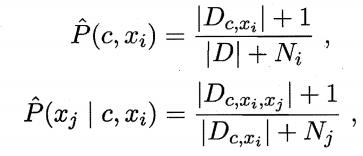
其中,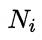 是第
是第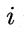 个属性可能的取值数,
个属性可能的取值数,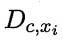 是类别为 c 且在第
是类别为 c 且在第 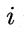 个属性上取值为
个属性上取值为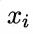 的样本集合,
的样本集合,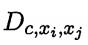 是类别为 c 且在第
是类别为 c 且在第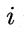 和第
和第 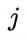 个属性上取值分别为
个属性上取值分别为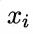 和
和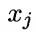 的样本集合。例如,对西瓜数据集3.0有
的样本集合。例如,对西瓜数据集3.0有
不难看出,与朴素贝叶斯分类器类似,AODE的训练过程也是“计数”,即在训练数据集上对符合条件的样本进行计数的过程。
既然将属性条件独立性假设放松为独依赖假设可能获得泛化性能的提升,那么,能否通过考虑属性间的高阶依赖(即对多个属性的依赖)来进一步提升泛化性能呢?实际上,若训练数据非常充分,泛化性能有可能提升;但在有限样本条件下,则又陷入估计高阶联合概率的泥沼。
【1】周志华 · 机器学习 · 清华大小出版社
【2】贝叶斯分类器(一):朴素贝叶斯分类器与半朴素贝叶斯分类器 http://blog.csdn.net/rongrongyaofeiqi/article/details/53100391
以上是关于19贝叶斯分类器:半朴素贝叶斯分类器(属性之间存在依赖)的主要内容,如果未能解决你的问题,请参考以下文章