巧克力里到底有没有红包?极简图解朴素贝叶斯分类
Posted Kira和极客们
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了巧克力里到底有没有红包?极简图解朴素贝叶斯分类相关的知识,希望对你有一定的参考价值。
你的APP每个月升级一次
你的头脑打算多久升级一次?
关注我,你比别人更靠近未来

「我们的目标是:要干货!还要看得懂!」
——Kira和极客们
被封面骗进来的各位,经过前两次隐马尔科夫模型的洗礼,大家是晕了还是升华了呢?

马上就要过年了,过年前让我们来轻松地学习点小知识吧,今天我们就来和大家讲讲朴素贝叶斯分类(Naive Bayes)。
它既然叫朴素,它就必然是“朴素”的,绝对不会像隐马尔可夫那么重口味,还是比较小清新的。
老规矩,作为“抽象概念”抵抗力0级物种,我们还是用例子给大家说明问题,毕竟“看得见摸得着”的才是我们这种吃瓜群众的最爱啊。
(下面是基础科普,熟悉条件概率的小伙伴们就跳过这段吧~~~)
我是告诉你以下是基础科普的分割线

我们先来讲讲什么是独立事件和联合概率。
马上就要过年了,你总要出去吃饭吧,而店家也往往会在这个时候推出各种活动,比如吃满多少钱可以抽奖。
假设你中午在饭店A吃饭抽中了大奖100元,晚上在和A饭店完全没有关系的饭店B吃饭又抽中了大奖200元。
一句话,你这天的运气好得不得了!因为如果假设饭店A中大奖的概率是1/100,饭店B中奖的概率是1/150,那么你一天之内两次吃饭都中奖的概率就是1/15000!
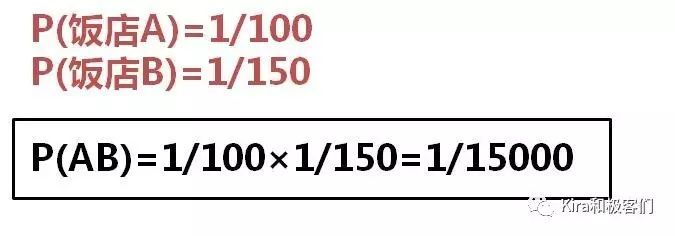
饭店A中奖和饭店B中奖是两个独立事件,也就是说这两家饭店之间没有半毛钱关系,B饭店的老板不会因为你在A饭店中奖了觉得你很厉害还故意让你在B饭店也中奖。
总之就是一句话,两个独立事件之间没有任何联系。
因此对于两个独立事件A和B,各自发生的概率是P(A)和P(B),它们同时发生的概率记为P(AB)(称为A和B的联合概率),那么:
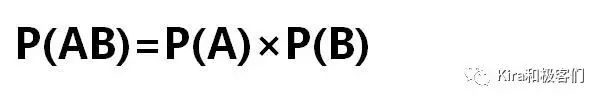
也就是说,独立事件的联合概率等于各自发生概率的乘积。
比如今天你去游乐园,遇到了几十年没见的老同学的概率就等于你去游乐园的概率乘以老同学去游乐园的概率。
(前提是你们事先没有互相联系,也没有任何渠道知道对方行动,这是两个独立事件。)
接下来我们来做一个盒子里选球的实验。
此时有两个盒子,盒子A和盒子B。盒子A里有8个红球,2个绿球。盒子B里有6个红球,4个绿球。
你闭着眼睛先选一个盒子,然后再从盒子里摸球,请问摸到红球的概率是多少?
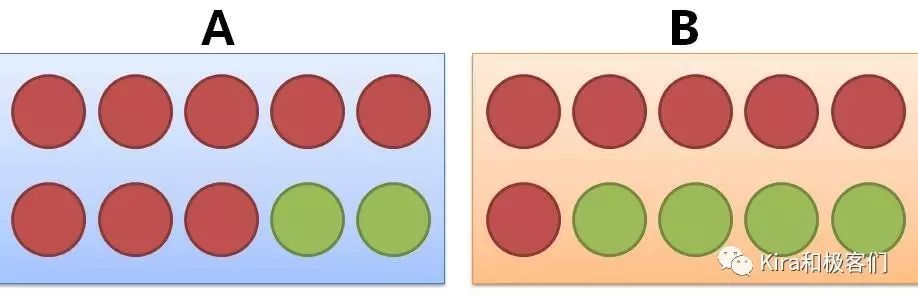
从实验条件中我们知道,首先,你需要在A和B里选中一个盒子,选中A和B的概率分别是1/2。
在A盒子里,红球占的比例是8/10,也就是说如果你选中的A盒子,那么摸到红球的概率是8/10。
这个8/10是在你选定A盒子后发生的概率,我们用X表示摸到红球的概率话,那X在选中A盒子后的概率记为P(X|A),表示X在A条件下的条件概率。
所以对于既要选中A盒子,又要摸到红球的概率P(X|A)是多少呢?
答案就是P(A)(选中盒子A的概率)× P(X|A)(选中盒子A以后摸到红球的概率)。
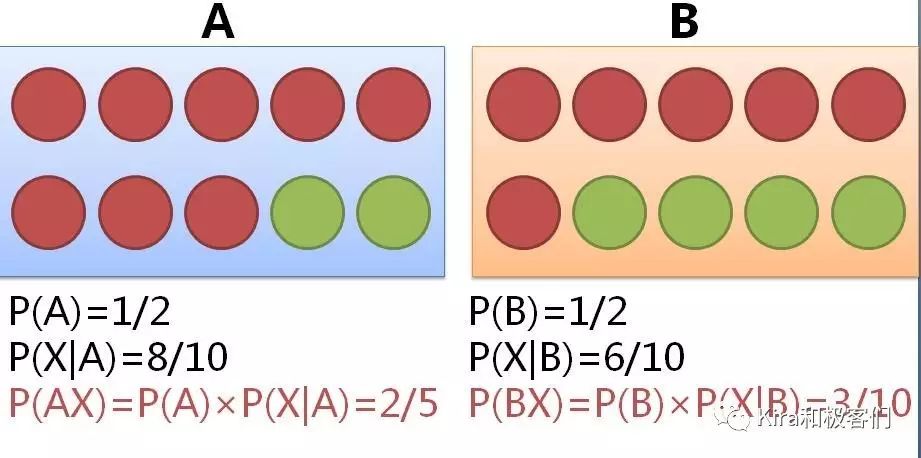
同理,如果你选中了B盒子,概率同样是1/2,而在B盒子里摸到红球的概率是6/10,因此P(X|B)表示在选中B盒子的条件下摸到红球的概率是6/10。
此时选中B盒子并摸到红球的概率就是1/2×6/10=3/10。
所以你闭着眼睛先选盒子再摸球,最终得到红球的概率P(X)就是选到A盒子摸到红球的概率加上选到B盒子摸到红球的概率。
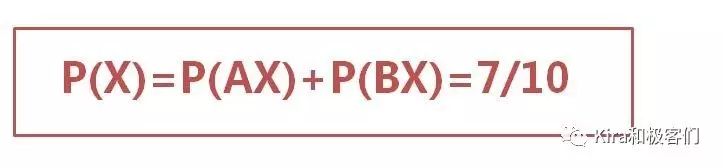
好了,现在我要反过来问这个问题:假设你闭着眼睛最终摸到了一个红球,请问这个红球到底是来自A还是来自B?
也就是说这个红球属于盒子A的概率和盒子B的概率分别是多少?
此时,我们需要求的是把已经摸到红球作为条件,问它是属于盒子A还是盒子B的条件概率。
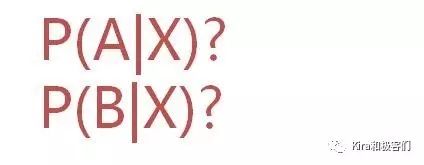
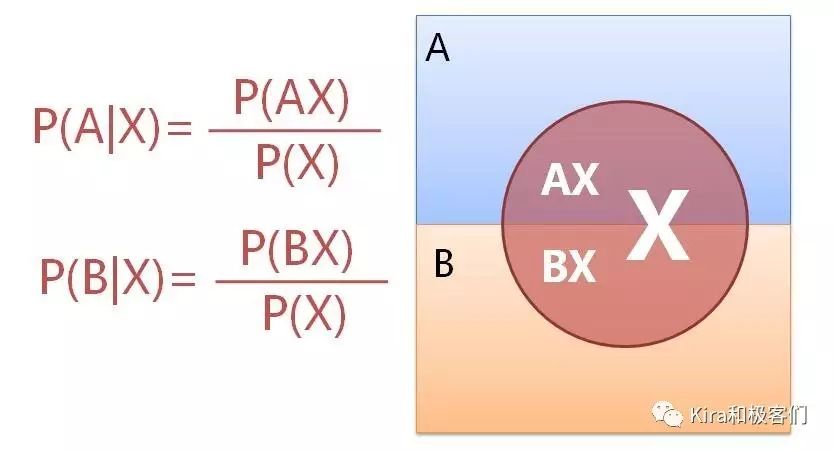
为了求解这个问题,我们来看一张图:
摸到红球的总概率P(X)是盒子A摸到红球的概率P(AX)和盒子B摸到红球的概率P(BX)的总和,所以显然P(AX)在P(X)中所占的比例就是就是盒子A中的红球对总的红球的贡献。
我们可以计算出P(AX)在P(X)中所占的比例,这个结果就是红球来自盒子A的概率P(A|X)。
如果大家还记得我们之前是如何计算P(AX)和P(BX)的话,一定可以发现:
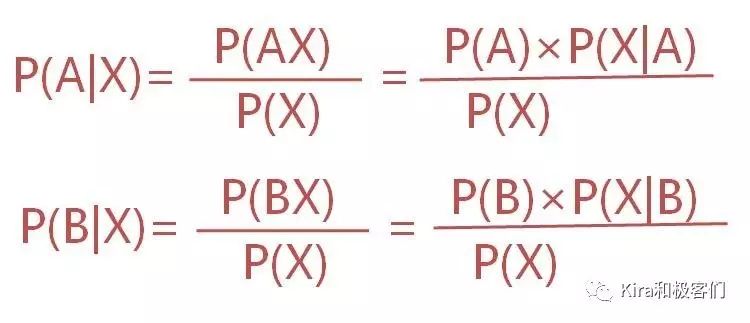
这是什么?这是贝叶斯公式啊!
所以贝叶斯公式的本质就是条件概率!
而贝叶斯公式最重要的精华是在于:你可以从事件X在事件A下的条件概率P(X|A)计算出事件A在事件X下的条件概率P(A|X)。
翻译成人话:就是可以从容易得到的条件概率求出不容易得到的条件概率。
等下你就知道这个看起来不过是条件概率颠来倒去的公式究竟有多神奇!
但是在开始之前我们再来讲最后一个概念,如果N个事件和某一事件相关,但是它们之间又是彼此独立,那么它们同时发生的条件概率可以用它们自己的条件概率计算。
解释不清楚,看图更清楚!
例如事件A1,A2,A3相互独立(彼此不影响),但是它们又与事件B相关,A1,A2,A3同时发生的条件概率等于各自的条件概率相乘。
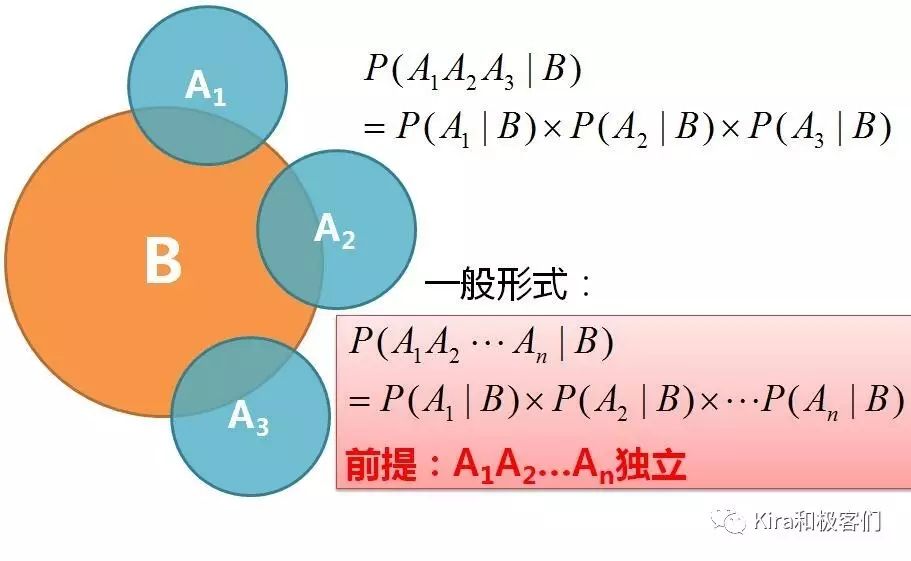
★注意,这里的前提条件是A1,A2,A3是独立事件!这个前提条件是朴素贝叶斯分类的重点!
我是告诉你基础科普已经结束的分割线

好了,搞清楚了贝叶斯公式,我们就来看看传说中的朴素贝叶斯分类吧。
我的经典台词:我们来看个例子。
马上就要过年了,大家有没有准备好年货啊?作为甜食控的吃货一族,巧克力是过年必备啊。
于是有家巧克力厂商就推出了买巧克力有机会得红包的活动。
(注意,以下开始都是我编的例子,你要是执着地问我到底哪家巧克力送红包,我就给你两个字,呵呵)
就是说只要你买一袋这个牌子的巧克力,里面就可能藏着红包。
不要和我吐槽这不像巧克力!
这个时候假设你是这家公司的商品调查员,就是负责记录顾客购买反馈信息的,比如顾客买了哪种巧克力,有没有抽到红包。。。
然后智商奇高无比机智聪明绝顶的你在记录了大量顾客反馈信息后发现:巧克力里面有没有红包好像和四个因素有那么点关系。
这些因素分别是巧克力的口味,生产日期,产地,还有包装。

这个时候,你的同事为了继续给公司做贡献,也买了一袋公司的巧克力:去年16年12月在上海加工厂生产的礼盒装抹茶巧克力。
买来后,你的同事还问你,你说我会中红包吗?
你默默地看了他一眼,说了一句无比装逼的话:我用朴素贝叶斯分类算一算。
(不要问我为什么不直接拆开......)
从上述的故事中我们知道巧克力和红包相关的特征X一共有四个:X1=口味,X2=生产日期,X3=产地,X4=包装类型,并且每个特征都有不同的属性。
比如口味有3个属性:X11=原味,X12=咖啡,X13=抹茶。
生产日期有2个属性,X21=16年11月,X22=16年12月。
......
这些巧克力一共可以分为2类:Y1=有红包,Y2=没红包。
所以我们要判断同事买的巧克力到底有没有红包其实也就是计算,在特征(X1,X2,X3,X4=抹茶,12月,上海,礼盒)的前提下,这袋巧克力有红包和没有红包的概率分别是多少,概率高的就是最终结果。

大家有没有对这个描述似曾相识?这就是计算类别Y在特征X下的条件概率啊!
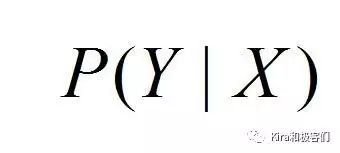
根据贝叶斯公式,这个条件概率可以这样计算:
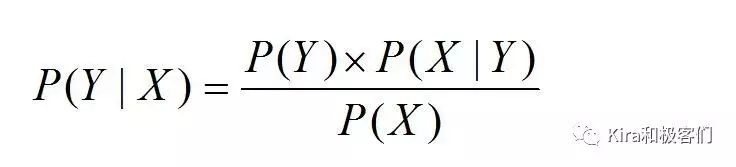
(不记得了请看前面的贝叶斯公式。)
也就是说,只要分别计算有红包的概率P(Y=有红包),特征X在有红包时的条件概率P(X=抹茶,12月,上海,礼盒|有红包),我们就可以得到一袋特征为X的巧克力有红包的概率。
(分母P(X)先不用管,因为无论对于有红包还是没有红包,P(X)都是一样的。分类是一个比大小的过程,所以直接看分子大小就可以。)
我们记录得到的数据是这样的:一共15组来自不同客户购买后反馈的数据。
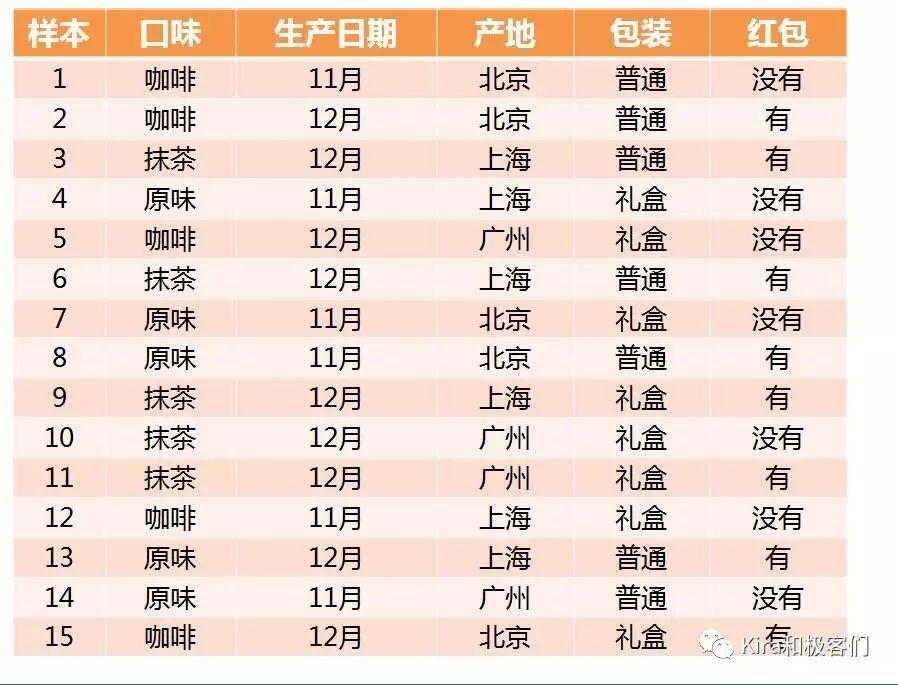
然后和上次隐马尔科夫模型的参数估计一样,我们直接“数一数”就能分别得到有红包和没有红包的概率。

大家回顾下之前提过的多个独立事件和某事件相关的概率计算公式,因此对于巧克力的4个特征,我们可以通过计算它们各自的条件概率得到。
(注意:假设这些特征相互独立是朴素贝叶斯分类的重要前提条件。一般来说,现实中的事件是不可能完全相互独立的,所以朴素贝叶斯分类在简洁、便于应用的同时也因为“独立假设”牺牲了一定的准确性。)
举例来说,在有红包条件下口味是“抹茶”的条件概率,就是在所有有红包的巧克力样本中寻找是“抹茶”口味的个数。
同理,有红包条件下,产地是“上海”的条件概率,就是“上海”在有红包的样本中占的比例。

所以对于其它特征,我们都可以这样数出来。
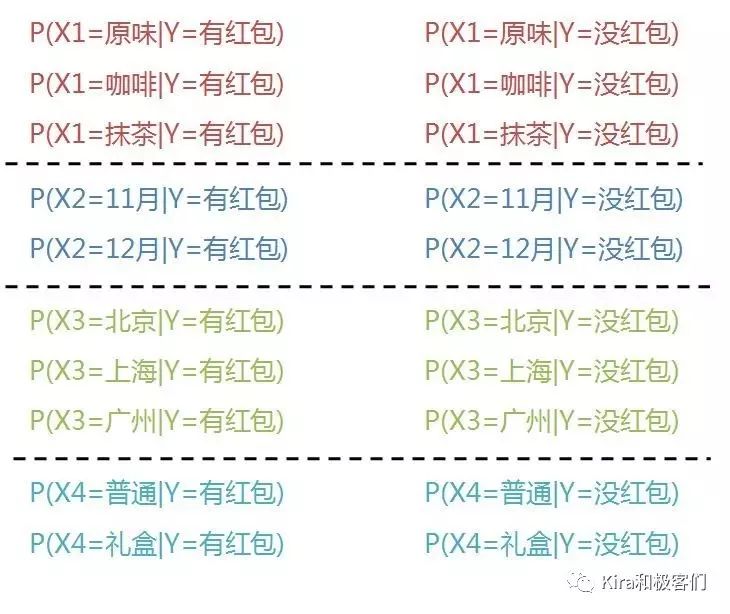
最终结果和数据都在一张图里,大家可以亲自数一数,看看你是否理解了这个“数”的概念,顺便帮我检查下有没有数错,谢谢~~~
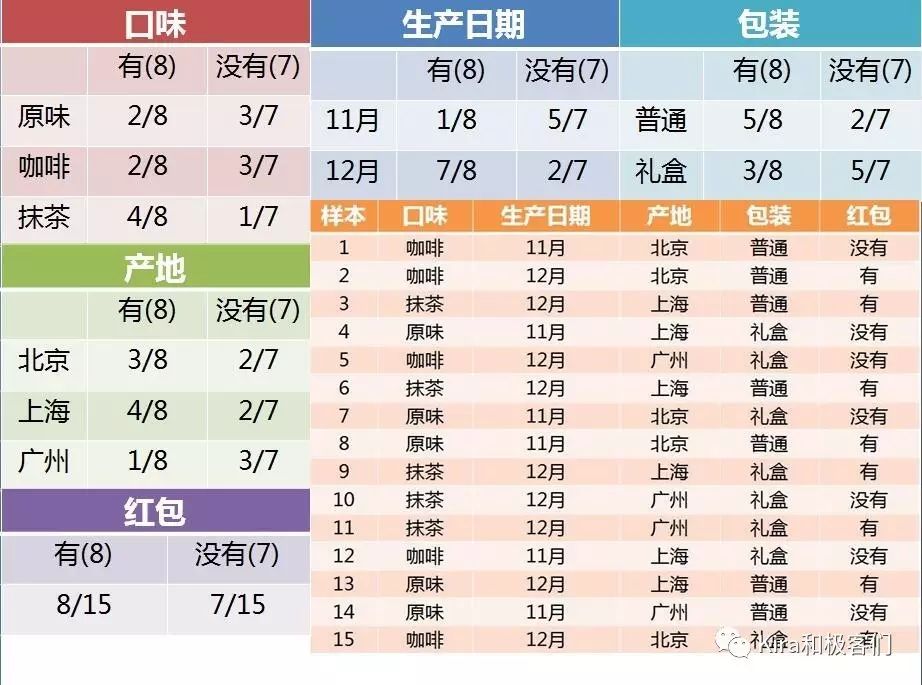
当然对于特征X(抹茶,12月,上海,礼盒装),其实你只需要数一下特征属性为抹茶,12月,上海和礼盒装时候的条件概率,但是为了给大家解释概念,这里是全部都列出了。
总之有了这些结果,就可以进行计算了。


你看,分母都是一样的,所以不用管它。
最后我们可以得到:

所以这袋同事买的去年16年12月在上海加工厂生产的礼盒装抹茶巧克力有红包的概率更高,就是说如果要分类的话,它应该是属于有红包的一类。
当然这个例子可能不太好,朴素贝叶斯分类一般用于更加直接的分类应用。
比如判断一封邮件是不是垃圾邮件这种,反正朴素贝叶斯在邮件分类上的科普文章很多,有兴趣的小伙伴可以自行查阅。
(如果你们要问那我为什么还要用这个巧克力的例子?我必须诚实地回答,因为快过年了,我的心中只有吃。。。)
总之,朴素贝叶斯分类就是一种“数一数”已知数据样本,来计算某个特征的样本应该属于的类别。
仔细的小伙伴一定会注意到这里面有个问题。
如果已知样本中没有“抹茶”这个属性出现在“有红包”,或者“没有红包”的样本中怎么办啊?
也就是说P(X1=抹茶|有红包)或者P(X1=抹茶|没有红包)=0,我们的计算中如果分子中的一项等于0,那么整体概率都是0。

然而这种判断是显然是不合理的,我们不能说因为一个现象没有观察到,所以这个事件就100%不可能发生。
万一随着数据的增加,下次它出现了呢?对于没有观察到的现象更加一般化地理解是,它发生的概率很小,但绝不是0。
(你不要和我说数学上概率为0表示依然存在很小的可能发生这种话。。。。我们这里是应用举例,你就当0表示绝对不可能发生。)
所以为了解决0概率的问题,我们在“数一数”的时候需要做拉普拉斯平滑。
大家不要怕,不是所有和拉普拉斯有关的东西都是复杂的。所谓拉普拉斯平滑只是在你数数的时候“加1”而已。
计算类别概率的时候,在分子上加1,分母则加上类别的个数。比如在我们例子中,只有2个类别,有红包和没有红包,所以分母加2(因为有红包和没红包的分子各加了1,等于总数加了2)。
如果是4个类别,比如学生成绩分为优良中差,那么分子还是加1,分母就是加4。
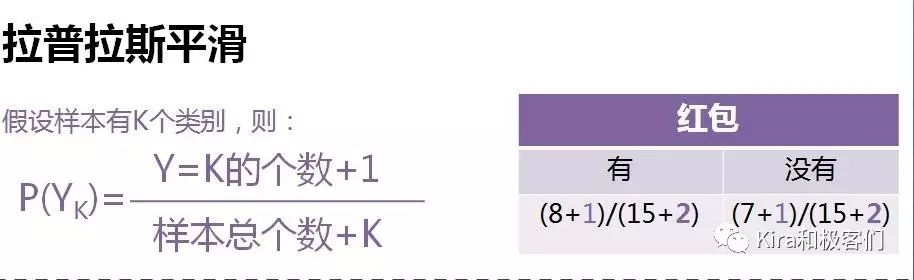
计算特征属性的条件概率时,也是一样,分子加1,这样就避免了0,然后有几个属性,分母就加上相应的个数。
比如对口味来说有3个属性,所以分母加3;对于生产日期来说,只有2个属性,所以分母加2。

这就是所谓拉普拉斯平滑了,接下来的计算方法和之前完全一样。
看到这里,其实你已经掌握了朴素贝叶斯分类,大家鼓掌,开始点赞。
最后,让我们来总结下朴素贝叶斯分类的特点。
首先朴素贝叶斯分类是基于贝叶斯公式,也就是条件概率。
其次,这种分类方法的重要前提条件是假设样本中的特征都是相互独立的,因此牺牲了一定的准确性。
再次,对于样本中可能出现0概率的情况应该采用拉普拉斯平滑处理。
朴素贝叶斯分类的基本应用过程如下:
决定你到底要分成哪些类别。
寻找和类别相关的特征。(这一步非常重要,所以能不能在一大堆数据中找到重要的特征往往决定了分类的准确性。)
计算类别概率P(Y);特征X在Y类别的条件概率P(X|Y)。
计算P(Y|X),选择X特征下,概率最大的类别作为样本的类。
好了,今天的小清新朴素贝叶斯分类就讲到这里,我要去吃(?)年货了~~~
由于我们是极简图解给大家科普,在讲解的过程中可能忽略了某些细节,所以有问题的小伙伴们请给我们留言。

参考资料:
1.《统计学习方法》李航,网上有电子版,我不多说了,你懂。
《极简科普》系列文章

END
原创文章,严禁私自转载
如有转载需求请后台回复“转载”,谢谢。
以上是关于巧克力里到底有没有红包?极简图解朴素贝叶斯分类的主要内容,如果未能解决你的问题,请参考以下文章