朴素贝叶斯分类器

Posted 2021-04-25 桂和杯大数据建模大赛

今日内容朴素贝叶斯分类器，我们从分类器、贝叶斯、朴素三方面来进行介绍。

首先分类器，顾名思义，即进行分类，我们可以通过这个算法来预测一个新来的个体属于哪一类。

然后是贝叶斯，封面这位就是托马斯·贝叶斯，他老人家证明了现在称为贝叶斯定理的一个特例。

也就是这么个定理：

贝叶斯定理：

这个定理解决了现实生活里经常遇到的问题：已知某条件概率，如何得到两个事件交换后的概率，也就是在已知P(A|B)的情况下如何求得P(B|A)。

这里再来解释一下条件概率：

P(A|B)就是B发生条件下A发生的概率，比如说黑人和非洲。P(黑人|非洲)就是已知他来自非洲的情况下，是黑人的概率。P(非洲|黑人)就是黑人中非洲人的概率。

一般来讲P(B|A)和P(A|B)的获取难度是不同的，这也就是贝叶斯定理的价值所在。仍然以黑人及非洲举例，P(黑人|非洲)就相对好统计，但是P(非洲|黑人)则不然，来了一个黑人哥，他可能是非洲，也可能是美洲，也可能是欧洲，等等。

这时贝叶斯定理就可以发挥作用。我们可以根据贝叶斯公式：

P(非洲|黑人)=P(黑人|非洲)*P（黑人）/P(非洲)

计算此概率。

最后，我们讲朴素。一个事情可能由多种原因决定，朴素就是假设这些原因是独立的。互不影响。一旦我们设定独立的条件，就可以把条件概率公式大大简化。经过一系列推导可以得到如下公式：

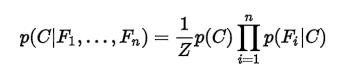
（详细推导可见https://zh.wikipedia.org/wiki/%E6%9C%B4%E7%B4%A0%E8%B4%9D%E5%8F%B6%E6%96%AF%E5%88%86%E7%B1%BB%E5%99%A8）

举个贝叶斯分类器的例子

（示例参考自：bilibili-av7719936）

假设我们想预测一个学生是否会挂科。首先，我们选择三个因素，比如说喝酒、逛街、和好好学习。现在来了一个学生不喝酒、不逛街还学习，预测他是否会挂科。

我们去做一个历史数据的统计，如图：

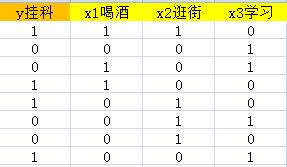
1表示做该项目，0表示不做该项目。

根据历史数据，计算P(x1|y)、P(x2|y)、P(x3|y)。之后对于待预测的学生：

分别计算

P(y=1|x1 x2 x3)和P(y=0|x1 x2 x3)

该学生不喝酒不逛街且学习，所以：

P(y=1|x1 x2 x3)=P(y=1|0 0 1)

朴素贝叶斯假设各因素独立，所以上式=

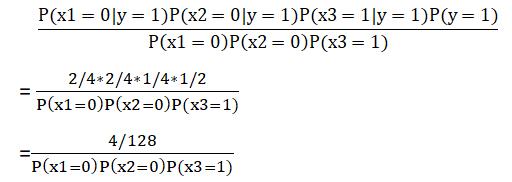
同理计算

P(y=0|x1 x2 x3)=P(y=0|0 0 1)

比较两者发现y=0即不挂科的概率较大。所以我们预测该生不挂科。

当然以上例子统计的样本数较少，实际生活中我们需统计大数量的样本来计算条件概率，可以更加准确。

朴素贝叶斯分类器虽然很简单，但在实际应用中可以取得不错的效果，对存在的少量异常点也不敏感。大家可以搜索更多资料了解一下。

数字人生，掘出战神

桂和杯大数据建模大赛

邮箱：[e-mail]