朴素贝叶斯分类：拉普拉斯修正

Posted 2021-04-25 算法channel

主要推送关于对算法的思考以及应用的消息。培养思维能力，注重过程，挖掘背后的原理，刨根问底。本着严谨和准确的态度，目标是撰写实用和启发性的文章，欢迎您的关注。

01

—

回顾

昨天的推送介绍了朴素贝叶斯分类的原理及阐述了一个例子，这种方法的预测发现了一个问题：某个样本的属性值并未出现在训练集中，导致尽管要预测的这个苹果看起来很像是好果，但是朴素贝叶斯目标函数的结果仍为0，最终被划分为一般的苹果，有些时候这并不是合理的，那么该如何解决呢？

如下的数据集：

#	大小	颜色	形状	标签
1	小	青色	非规则	否
2	大	红色	非规则	是
3	大	红色	圆形	是
4	大	青色	圆形	否
5	大	青色	非规则	否
6	小	红色	圆形	是
7	大	青色	非规则	否
8	小	红色	非规则	否
9	小	青色	圆形	否
10	大	红色	圆形	是

测试集上要预测的某个样本如下：

#	大小	颜色	形状	标签
11	大	青色	圆形	?

02

—

拉普拉斯修正

上面通过这个例子折射处一个问题：训练集上，很多样本的取值可能并不在其中，但是这不并代表这种情况发生的概率为0，因为未被观测到，并不代表出现的概率为0 。

正如上面的样本，看其他两个属性很可能属于好苹果，但是再加上颜色：青色，这三个属性取值组合在训练集中并未出现过，所以朴素贝叶斯分类后，这个属性取值的信息抹掉了其他两个属性的取值，在概率估计时，通常解决这个问题的方法是要进行平滑处理，常用拉普拉斯修正。

拉普拉斯修正的含义是，在训练集中总共的分类数，用 N 表示；di 属性可能的取值数用 Ni 表示，因此原来的先验概率 P(c) 的计算公式由：

被拉普拉斯修正为：

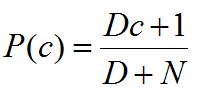
类的条件概率P(x | c) 的计算公式由：

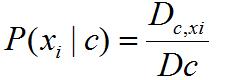
被拉普拉斯修正为：

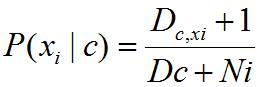
03

—

例子阐述

在拉普拉斯修正后，本文提到的预测样本预测的结果会不会还是一般的果子呢？（因为好果的概率因为某项乘积为0，所以导致最终结果为0）

#	大小	颜色	形状	标签
11	大	青色	圆形	?

用拉普拉斯修正后的公式计算，先验概率 P(c) ，

P(c = 好果）=  (4+1) / (10+2) = 5/12

P(c = 一般) = (6+1) / (10+2) = 7/12

每个属性的类条件概率：

P(大小=大 | c=好果) =   (3+1)/(4+2) = 4/6

P(颜色=青色 | c=好果) = (0+1）/(4+2) = 1/6

P(形状=圆形 | c=好果) = (3+1) / (4+2) = 4/6

P(大小=大 | c=一般) =  (3+1) /( 6+2) = 4/8

P(颜色=青色 | c=一般) = (5+1)/(6+2) = 6/8

P(形状=圆形 | c=一般) =  (2+1)/(6+2) = 3/8

因此：  

P(c=好果） * P(大小=大 | c=好果) * P(颜色=青色 | c=好果) * P(形状=圆形 | c=好果)  

= 5/12 * 4/6 * 1/6 * 4/6 

= 0.031

P(c=一般） * P(大小=大 | c=一般) * P(颜色=红色 | c=一般) * P(形状=圆形 | c=一般)  

= 7/12 * 4/8 * 6/8 * 3/8

= 0.082

因此预测结果还是一般的果子，这是训练集学习后得到的结果，可能与原来的结果正好吻合，但是并不代表拉普拉斯修正是没有必要的，有时候预测的结果会和原来直接某项为0的结果不一样，可以看到拉普拉斯修正后，原来为0的结果被平滑的过渡为0.031，这起到了修正的作用。

04

—

展望

以上总计了朴素贝叶斯分类器的基本原理，并用一个简单的例子进行了说明。注意到它有一个假定为：各个属性条件是独立的假设，但是在现实任务中此假设往往难以成立，可不可以对这个假设进行一定程度的放松呢？ 对此假设的放松产生了一种分类算法：半朴素贝叶斯分类。请看明天的推送，半朴素贝叶斯分类原理解析。

谢谢您的阅读！

更多文章：

请记住：每天一小步，日积月累一大步！

交流思想，注重分析，看重过程，包含但不限于：经典算法，机器学习，深度学习，LeetCode 题解，Kaggle 实战，英语沙龙，定期邀请专家发推。期待您的到来！