机器学习：说说贝叶斯分类

Posted 2021-04-25 算法channel

编辑：Emily

1 进入例子

假如我是一个质检员，现在接到了三箱零件需要检验，其中第一箱有10个零件，第二箱有20个零件，第三箱有15个。半小时过去了，检验的结果出炉，第一箱有1个不合格，第二箱有3个不合格，第三箱2个不合格。

下午领导要来视察了，看看我验的货到底有没有问题，于是他随手拿了一个零件，我心里默默计算，领导拿到这个件为合格件的概率有多大？

在这个问题中，领导拿的这个零件首先一定在这3个箱子中的某一个，因此样本空间可以由这3个箱子组成，记 Ai 为从第i个箱子拿的零件，i的取值范围为1,2,3。然后再用一个事件来标记拿到正品，记为B，因此，领导拿到这个件为合格件的概率，记为 P(B)。

那么这个P(B)等于多少呢？这个事件B的发生肯定来自于样本空间吧，也就是说这个合格件要么从A1，A2，或者A3中获取到，因此，

 P(B) = P(A1)*P(B | A1) + P(A2) *P(B | A2) + P(A3)*P(B | A3)

                    = (1/3) * 9/10 + (1/3) * 17/20 + (1/3) * 13/15 

                    =  0.872

上面P(B | A1) 是条件概率：零件来自于第一个箱子的条件下，并且它为合格件的概率。

果不其然，领导抽到了一个合格品，然后他亲自检验了下，发现质检的没有问题，冲着我笑了笑，很满意地拍拍屁股就走人了。

当他走了的时候，我想到了一个问题，领导抽的这个合格品来自于箱子1的概率是多大呢？这个问题也就是求 P(A1 | B)，即取到合格品事件B发生了地情况下，来自于A1的概率。

求P(A1 | B)称为求解逆向概率，这个概率往往是不好求解答，但是它对应的正向概率：P(B | A1)，往往求解简单。

因此，自然地，既然 P(A1|B)比较难求解，我们如下转化一下：

P(A1| B) =  P(A1*B) / P(B) 

其中，A1*B 事件表示从第一个箱子抽取且为合格件，则

 P(A1*B) = P(A1) * P(B | A1) = (1/3) * 9/10 =  0.3 

P(A1*B)，也可以记为：P(A1,B)，它称为联合概率。

因此，P(A1| B) =  0.3  / 0.872 = 0.344 

这个已知B发生，然后，预测B来自于哪里，便是贝叶斯公式做的事情。

那么这个例子如何上升进而提取出一个模型出来呢？

2 例子引出贝叶斯公式

以上《合格品的例子》的样本空间有 A1，A2 ，A3 组成，它们把样本空间划分为三部分。

如果将划分上升到由 n 个部分组成，抽中一个合格件为本次随机试验的事件B，明显地，P(Ai) 和 P(B)都大于零，则事件B发生后，找出它属于哪个类别的计算公式如下：

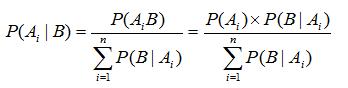
贝叶斯公式是要找出组成发生事件B的各个样本空间，然后预测事件B的发生来自于Ai的概率。

其中 P(Ai) 称为原因的先验概率，可以看到它是在不知道事件B是否发生的情况下获取的概率。比如在抽取零件时，我们不知道能不能抽取到合格件，但是选择任意一个箱子的概率一定都为1/3，所以称为先验概率。

而 P(Ai | B) 是原因的后验概率，它是在知道了事件B发生的条件下，有了这个进一步的信息后，判断原因 Ai 发生的概率有多大。可以看到，一般地，如果对样本空间做了大于1的划分，即：

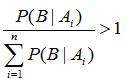
所以根据上面提到贝叶斯公式，不难推断出：

这也就是说在获取了进一步的信息B后，原因的后验概率一般大于原因的先验概率。

3 例子看贝叶斯决策

根据北平市第一实验中学101班历年的统计数据，班上努力学习的学生占到90%，并标记这部分群体为A0类，学习不用功的占到10%，并标记这部分群体为A1类。因此将学生群体划分为两类：

1. 学习努力的学生

2. 学习不努力的学生

再根据历年的升学率，学生只要学生努力学习考上重点大学的概率为 0.7，而不努力的学生考上重点大学的概率为 0.01 。

目标是预测以下两个问题：

1. 当一个学生考上重点大学时，这个学生属于群体A0的概率？

2. 当一个学生考上重点大学时，这个学生属于群体A1的概率？

---

求解过程

定义一个事件B：学生考上重点大学，其发生的概率为P(B)，该样本空间被划分为两类：A0和A1，则 P(B) = P(B | A0) + P(B | A1)  = 0.71 

这个学生考上重点大学条件下且来自群体A0的概率标记为：P(A0 | B ) 。

由贝叶斯公式可知，

这个考上重点大学的学生属于群体A0的概率： P(A0 | B ) 

= P(A0 * B) / P(B) 

= P(A0) * P(B | A0)  / 0.71

= 0.9 * 0.7 / 0.71

= 0.887

同理，这个考上重点大学的学生属于群体A1的概率：P(A1 | B ) 

= P(A1 * B) / P(B) 

= P(A1) * P(B | A1)  /  0.71

= 0.1 * 0.01 /  0.71

= 0.0014

可以看出，这个学生属于努力学习那个圈里头的概率为0.887，属于不努力学习圈的概率为0.0014，换言之，不努力学习还能上重点的概率是一千人里出一个多的天才，这就是根据贝叶斯公式做出的预测。

4 总结和展望

用一个合格零件判断来自哪个箱子的例子引出贝叶斯公式，然后解释贝叶斯公式和其中涉及的两个概念：先验概率和后验概率，最后用一个很直接的例子说明如何用贝叶斯做分类。

注意到在贝叶斯公式中，要求后验概率 P(classification | data) ，利用贝叶斯公式将其其转化为求解 ：

P(classification) * P(data | classification) / P(data)

这次求解模式在机器学习中被称为：生成式（generative models）模式。

注意到 

P(data) 是与类标记无关的量，可以看做是一个常数；

P(classification) 表达了各类样本所占的比例，根据大数定律，当训练集包含了充足的独立同分布样本时，P(classification)可以通过各类样本出现的频率来进行估计。

您知道 P(data | classification) 即 data相对于classification的概率怎么计算吗？ 如果一旦我们知道了它的求解方法，那么贝叶斯公式分类预测算法的核心就掌握了。预知其答案，求关注明天的推送！

谢谢您的阅读！ 

交流思想，注重分析，看重过程，包含但不限于：经典算法，机器学习，深度学习，LeetCode 题解，Kaggle 实战，英语沙龙，定期邀请专家发推。期待您的到来！