最基础的分类算法-朴素贝叶斯分类

Posted 2021-04-25 歌老师的小笔记本

文末福利，帮你学会构造朴素贝叶斯分类器的数据和代码。

---

最近跟其他人交流的，听说有一个人面试的时候解释了线性回归和朴素贝叶斯分类器以后直接拿下offer，于是我决定讲一讲这个听上去就很奇怪的分类算法。

解释一下贝叶斯公式，有概率论基础的同学应该不难理解。

先看条件概率，条件概率指的是一件事发生的情况下另一件事发生的概率：

这个式子左边这个符号指的就是条件概率，用中文说，就是事件B发生的情况下A发生的概率；右面这个分式呢，分母是事件B发生的概率，分子是事件A、B都发生的概率。

理解不了的同学看这里啦，我们想象这样一个过程，扔一个骰子，我们把数字1朝上或者数字3朝上记作事件A，就是说我扔一次，朝上的是1，我们可以说事件A发生了，再扔一次，朝上的是3，这一次事件A也发生了，那么P(A)=2/6=1/3。同理把数字1或者数字2朝上记作事件B，则P(B)=2/6=1/3。

事件AB都发生表示什么呢，分开看，事件B发生了表示朝上的是1或者2，事件A发生了表示朝上的是1或者3，那么AB都发生就表示朝上的是1，也就说P(AB)=1/6。

现在换个玩法，扔了一次以后不告诉你朝上的数字是几，但是告诉你事件B发生了，意味着什么呢，朝上的不是1就是2，那么这个时候事件A发生的概率就表示为P(A|B)，这个值是多少呢，不是1就是2，是1还是2又是等概率的，这个时候只有朝上的是1，A事件才是发生了，所以P(A|B)就等于1/2。

为什么是这样的呢？因为当我们知道B发生的时候，再计算A的概率的时候，可能发生的事件数目就少了，剩余可能的事件数恰好是之前事件数乘上P(B)，相应地，我们计算的概率就要用P(AB)除以P(B)。

然后呢，把这个公式变一下，写成下面这个样子：

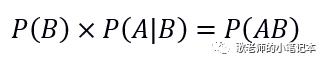
同样的，我们也有这个式子：

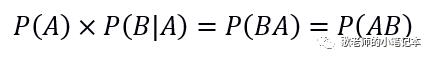
把上面两个式子连起来再做个简单的变换，得到下面这个公式，就叫贝叶斯公式啦：

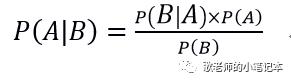
整个算法呢，都是依据着这个公式来的。

怎么运用这个公式呢，我们来看一个分类问题：

这是一个有关汽车测评的数据集，我们要做的是根据汽车的六个属性buying、maint、doors、persons、lug_boot、safaty确定其所属的类别class。表格中列代表一个属性，每一行代表一个已知属性的汽车和其正确的分类，当然我们的任务是给一些待分类的汽车，根据他们这六个属性的情况，确定类别。

假设有一辆待分类的汽车属性是这样的：

buying: Vhigh; 

maint: Med;

doors: 3; 

persons: 4; 

lug_boot: Med; 

safety: high

想确定他的class应该是属于Unacc 还是Acc。

思路是这样的，我们分别求一下在这样的属性取值下类别是Unacc和Acc的概率，哪个大，就把类别定为哪一类，这个时候，分类情况就是事件A，属性取值就是事件B。

 

先看第一种情况：

定义两个事件：

    事件A：该汽车分类为Unacc

    事件B：该汽车属性如下：

    buying: Vhigh; maint: Med; doors: 3; persons: 4; lug_boot:Med; safety:High

这个时候我们求的就是条件概率：

现在来看的话，如果我们知道了P(B|A)、P(A)、P(B)，把他们代到公式里面去就可以得到答案啦。

首先来看最简单的，P(A)，表示什么呢，表示一辆汽车被分类为Unacc的概率，注意哦，这里说的被分类为Uacc的概率指的是任何一辆汽车被分类为Unacc的概率，跟我们现在要计算的条件概率P(A|B)是不一样的。这个时候就用到我们已有的数据集啦，我们认为，已有数据集中出现Unacc的频率除以已有数据集中的样本个数就是P(A)，也就是说，如果表格中的数据是全部数据集的话，这个时候P(A)=5/7。

再来看P(B|A)，为了方便呢，我们定义几个新的事件：

    事件B1：buying = Vhigh

    事件B2：maint = Med

    事件B3：doors = 3

    事件B4：persons = 4

    事件B5：log_boot = Med

    事件B6：safety = High

这个时候P(B|A)就可以写成这个样子：P(B1,B2,B3,B4,B5,B6|A)，什么意思呢就是说事件A发生的条件下事件B1-B6都发生的概率，也就是之前的事件B发生的概率。

这个时候要解释一下什么叫“朴素”，你贝叶斯就贝叶斯，朴素又是什么意思呢？

这里的“朴素”说的是我这个样本啊，不同属性在取值上相互之间是没有任何的影响的。举个例子，本例中buying属性取什么值，对其他属性没有任何影响。这就是朴素的含义。

那么如果属性之间朴素了，怎么样呢，就有这么一个关系：

P(B1,B2,B3,B4,B5,B6| A) = P(B1|A)*P(B2|A)*P(B3|A)*P(B4|A)*P(B5|A)*P(B6|A)

这个公式叫做全概率公式，只要是“朴素”的，全概率公式就成立，没有必要钻牛角尖去理解这个公式，只要知道满足什么条件可以用这个公式就OK啦。

我们再来看怎么求P(B1 | A)呢，类似求P(A)的方法，我们可以从数据集中得到，按照条件概率的定义，P(B1 | A)表示A发生的条件下B1发生的概率，也就是说一辆车是属于Unacc的情况下，它的buying属性为Vhigh的概率，那我们把数据集中所有Unacc类别的汽车拿出来，看看有几个的buying属性是Vhigh，再除以Unacc类别汽车的数量就可以啦，同样的，按照表格中的数据呢，P(B1 | A) = 2/5，这样一点一点就可以把P(B | A)的值求出来啦。

还有一个P(B)，这里呢我们先不求，先看第二种情况：

第二种情况下

    事件A：该汽车分类为Acc

    事件B：该汽车属性如下：

buying: Vhigh; maint: Med; doors: 3; persons: 4; lug_boot:Med; safety: High

类似上面那个过程，也可以求得这个时候的P(A)、P(B | A)，不过我们发现一个有趣的事情，这两种情况里，事件B 的定义是完全一样的，也就是说两种情况下P(B)的相等的。我们要做到呢，其实并不是要求两种情况下的P(A|B)具体数值，只是说比较两者的大小，哪个大就把汽车分在哪一类，所以我们完全没必要求P(B)的具体数值啊，反正两个数都除以一个大于0的数，他们的大小关系不变，所以P(B)是我们不用花时间去计算的。

 

下一步呢，就比较复杂了，算了不吓唬大家了，下一步比较大小就可以了。

 

同样，我也花时间做了一个关于朴素贝叶斯分类器的练习，有代码有数据，后台回复“朴素贝叶斯”获取。

 

至此，朴素贝叶斯分类器的原理就介绍完啦，当然还有一些其他的问题没有涉及，之后也会一点一点讲到的，解释的婆婆妈妈，其实是想通过大白话让大家能更好地理解，毕竟一些太专业的公式定理理解起来还是有点无聊的，觉得讲得好可以关注和转发～不好的或者没理解地方可以后台直接提问！