贝叶斯分类算法
Posted Python之王
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了贝叶斯分类算法相关的知识,希望对你有一定的参考价值。
贝叶斯分类算法
贝叶斯分类算法是统计学的一种分类方法,它是一类利用概率统计知识进行分类的算法。在许多场合,朴素贝叶斯(Naïve Bayes,NB)分类算法可以与决策树和神经网络分类算法相媲美,该算法能运用到大型数据库中,而且方法简单、分类准确率高、速度快。
贝叶斯原理概念:
一、先验概率:
通过经验来判断事情发生的概率 ,比如说“贝叶死”的发病率是万分之一,就是先验概率。再比如南方的梅雨季是 6-7 月,就是通过往年的气候总结出来的经验,这个时候下雨的概率就比其他时间高出很多。
二、后验概率:
后验概率就是发生结果之后,推测原因的概率。 比如说某人查出来了患有“贝叶死”,那么患病的原因可能是 A、B 或 C。患有“贝叶死”是因为原因 A 的概率就是后验概率。它是属于条件概率的一种。
三、条件概率:
事件 A 在另外一个事件 B 已经发生条件下的发生概率, 表示为 P(A|B),读作“在 B 发生的条件下 A 发生的概率”。比如原因 A 的条件下,患有“贝叶死”的概率,就是条件概率。
朴素贝叶斯算法
设每个数据样本用一个n维特征向量来描述n个属性的值,即:X={x1,x2,…,xn},假定有m个类,分别用C1, C2,…,Cm表示。给定一个未知的数据样本X(即没有类标号),若朴素贝叶斯分类法将未知的样本X分配给类Ci,则一定是
根据贝叶斯定理
由于P(X)对于所有类为常数,最大化后验概率P(Ci|X)可转化为最大化先验概率P(X|Ci)P(Ci)。
如果训练数据集有许多属性和元组,计算P(X|Ci)的开销可能非常大,为此,通常假设各属性的取值互相独立,这样
先验概率P(x1|Ci),P(x2|Ci),…,P(xn|Ci)可以从训练数据集求得。
根据此方法,对一个未知类别的样本X,可以先分别计算出X属于每一个类别Ci的概率P(X|Ci)P(Ci),然后选择其中概率最大的类别作为其类别。
朴素贝叶斯算法成立的前提是各属性之间互相独立。当数据集满足这种独立性假设时,分类的准确度较高,否则可能较低。另外,该算法没有分类规则输出。
在贝叶斯分类中,我们感兴趣的是在给定一些观察到的特征的情况下找到标签的概率,我们可以将这些特征写成P(L | features)P(L | features) 。贝叶斯定理告诉我们如
P(L | features)=P(features | L)P(L)P(features)
P(L | features)=P(features | L)P(L)P(features)
在两个标签之间做出决定,我们称它们为L1L1 和L2L2,那么做出这个决定的一种方法是计算每个标签的后验概率之比
P(L1 | features)P(L2 | features)=P(features | L1)P(features | L2)P(L1)P(L2)
P(L1 | features)P(L2 | features)=P(features | L1)P(features | L2)P(L1)P(L2)
Sklearn提供了3个朴素贝叶斯算法:
高斯朴素贝叶斯:特征变量是连续变量,符合高斯分布,比如说人的身高,物体的长度。
多项式朴素贝叶斯:特征变量是离散变量,符合多项分布,在文档分类中特征变量体现在一个单词出现的次数,或者是单词的 TF-IDF 值等。
伯努利朴素贝叶斯:特征变量是布尔变量,符合 0/1 分布,在文档分类中特征是单词是否出现。
代码开干
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
先生成数据
from sklearn.datasets import make_blobs
X, y = make_blobs(100, 2, centers=2, random_state=2, cluster_std=1.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu');
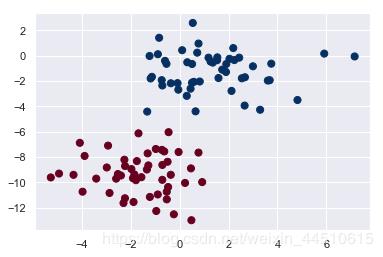
在使用MultinomialNB分类器训练时,如果输入数据出现负值,会出现"ValueError: Input X must be non-negative"的错误。解决办法,将MultinomialNB换成 GaussianNB即可。
这种朴素高斯假设的结果如下图所示:
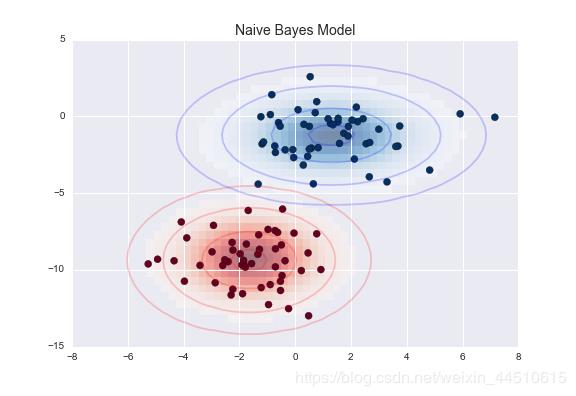
这里的椭圆代表每个标签的高斯生成模型,有更大的概率朝向椭圆的中心
高斯朴素贝叶斯
英文名:Gaussian Naive Bayes
导入高斯朴素贝叶斯模型
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(X, y)
预测新数据的分类
rng = np.random.RandomState(0)
Xnew = [-6, -14] + [14, 18] * rng.rand(2000, 2)
ynew = model.predict(Xnew)
ynew
# array([1, 1, 1, ..., 0, 1, 1])
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='RdBu')
lim = plt.axis()
plt.scatter(Xnew[:, 0], Xnew[:, 1], c=ynew, s=20, cmap='RdBu', alpha=0.1)
plt.axis(lim)
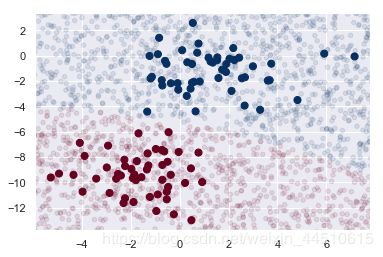
在比如有些特征可能是连续型变量,比如说人的身高,物体的长度,这些特征可以转换成离散型的值,比如如果身高在160cm以下,特征值为1;在160cm和170cm之间,特征值为2;在170cm之上,特征值为3。也可以这样转换,将身高转换为3个特征,分别是f1、f2、f3,如果身高是160cm以下,这三个特征的值分别是1、0、0,若身高在170cm之上,这三个特征的值分别是0、0、1。不过这些方式都不够细腻,高斯模型可以解决这个问题。高斯模型假设这些一个特征的所有属于某个类别的观测值符合高斯分布
下面是高斯朴素贝叶斯模型处理iris数据集
>>> from sklearn import datasets
>>> iris = datasets.load_iris()
>>> iris.feature_names # 四个特征的名字
['sepal length (cm)', 'sepal width (cm)', 'petal length (cm)', 'petal width (cm)']
>>> iris.data
array([[ 5.1, 3.5, 1.4, 0.2],
[ 4.9, 3. , 1.4, 0.2],
[ 4.7, 3.2, 1.3, 0.2],
[ 4.6, 3.1, 1.5, 0.2],
[ 5. , 3.6, 1.4, 0.2],
[ 5.4, 3.9, 1.7, 0.4],
[ 4.6, 3.4, 1.4, 0.3],
[ 5. , 3.4, 1.5, 0.2],
......
[ 6.5, 3. , 5.2, 2. ],
[ 6.2, 3.4, 5.4, 2.3],
[ 5.9, 3. , 5.1, 1.8]]) #类型是numpy.array
>>> iris.data.size
600 #共600/4=150个样本
>>> iris.target_names
array(['setosa', 'versicolor', 'virginica'],
dtype='|S10')
>>> iris.target
array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0,....., 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, ......, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2])
>>> iris.target.size
150
>>> from sklearn.naive_bayes import GaussianNB
>>> clf = GaussianNB()
>>> clf.fit(iris.data, iris.target)
>>> clf.predict(iris.data[0])
array([0]) # 预测正确
>>> clf.predict(iris.data[149])
array([2]) # 预测正确
>>> data = numpy.array([6,4,6,2])
>>> clf.predict(data)
array([2]) # 预测结果很合理
多项式朴素贝叶斯
除了高斯朴素贝叶斯,另一个有用的例子是多项式朴素贝叶斯(naive bayes),其中假定特征是由简单的多项式分布生成的。多项式分布描述了在许多类别中观察计数的概率,因此多项式朴素贝叶斯最适合表示计数或计数率的特征。
举例叙说多项式朴素贝叶斯
收集大量的垃圾邮件和非垃圾邮件,建立垃圾邮件集和非垃圾邮件集。
提取邮件主题和邮件体中的独立字符串,例如 ABC32,¥234等作为TOKEN串并统计提取出的TOKEN串出现的次数即字频。按照上述的方法分别处理垃圾邮件集和非垃圾邮件集中的所有邮件。
每一个邮件集对应一个哈希表,hashtable_good对应非垃圾邮件集而hashtable_bad对应垃圾邮件集。表中存储TOKEN串到字频的映射关系。
计算每个哈希表中TOKEN串出现的概率P=(某TOKEN串的字频)/(对应哈希表的长度)。
综合考虑hashtable_good和hashtable_bad,推断出当新来的邮件中出现某个TOKEN串时,该新邮件为垃圾邮件的概率。数学表达式为:
A 事件 ---- 邮件为垃圾邮件;
t1,t2 …….tn 代表 TOKEN 串
则 P ( A|ti )表示在邮件中出现 TOKEN 串 ti 时,该邮件为垃圾邮件的概率。
设
P1 ( ti ) = ( ti 在 hashtable_good 中的值)
P2 ( ti ) = ( ti 在 hashtable_ bad 中的值)
则 P ( A|ti ) =P2 ( ti ) /[ ( P1 ( ti ) +P2 ( ti ) ] ;建立新的哈希表hashtable_probability存储TOKEN串ti到P(A|ti)的映射。
至此,垃圾邮件集和非垃圾邮件集的学习过程结束。根据建立的哈希表 hashtable_probability可以估计一封新到的邮件为垃圾邮件的可能性。
当新到一封邮件时,按照步骤2,生成TOKEN串。查询hashtable_probability得到该TOKEN 串的键值。
假设由该邮件共得到N个TOKEN 串,t1,t2…….tn,hashtable_probability中对应的值为 P1 , P2 , ……PN, P(A|t1 ,t2, t3……tn) 表示在邮件中同时出现多个TOKEN串t1,t2……tn时,该邮件为垃圾邮件的概率。
由复合概率公式可得P(A|t1 ,t2, t3……tn)=(P1P2……PN)/[P1P2……PN+(1-P1)(1-P2)……(1-PN)],当 P(A|t1 ,t2, t3……tn) 超过预定阈值时,就可以判断邮件为垃圾邮件。
该模型常用于文本分类,特征是单词,值是单词的出现次数。
TF-IDF值:
词频 TF 计算了一个单词在文档中出现的次数,它认为一个单词的重要性和它在文档中出现的次数呈正比。
计算公式:词频 TF=单词出现的次数/该文档的总单词数
逆向文档频率 IDF ,是指一个单词在文档中的区分度。它认为一个单词出现在的文档数越少,就越能通过这个单词把该文档和其他文档区分开。IDF 越大就代表该单词的区分度越大。
计算公式:逆向文档频率 IDF=log(文档总数/该单词出现的文档数+1)
TF-IDF 实际上是词频 TF 和逆向文档频率 IDF 的乘积 。这样我们倾向于找到 TF 和 IDF 取值都高的单词作为区分,即这个单词在一个文档中出现的次数多,同时又很少出现在其他文档中。这样的单词适合用于分类。
例子
假设一个文件夹里一共有 10 篇文档,其中一篇文档有 1000 个单词,“this”这个单词出现 20 次,“bayes”出现了 5 次。“this”在所有文档中均出现过,而“bayes”只在 2 篇文档中出现过。我们来计算一下这两个词语的 TF-IDF 值。
针对“this”,计算 TF-IDF 值:
词频 TF =20/100=0.02
逆向文档频率 IDF = log(10/10+1)=-0.0414
TF-IDF=0.02*(-0.0414)=-8.28e-4。
针对“bayes”,计算 TF-IDF 值:
词频 TF =5/1000=0.005
逆向文档频率 IDF = log(10/2+1)=0.5229
TF-IDF=0.005 * 0.5229=2.61e-3。
总结:
“bayes”的 TF-IDF 值要大于“this”的 TF-IDF 值。这就说明用“bayes”这个单词做区分比单词“this”要好。
案例:如何对文档进行分类:
从文本中提取特征信息 CountVectorizer类和TfidfVectorizer类
CountVectorizer和TfidfVectorizer方法的不同:
CountVectorizer__ 和 _TfidfVectorizer_ 是 __文本特征提取 的两种方法。两者的主要区别在于,CountVectorizer仅仅通过计算词语词频,没有考虑该词语是否有代表性。而TfidfVectorizer可以更加精准的表征一个词语对某个话题的代表性。
sklearn中的fit,transform,fit_transform 在文本提取特征中各自的作用。
首先,计算机是不能从文本字符串中发现规律。只有将字符串编码为计算机可以理解的数字,计算机才有可能发现文本中的规律。
对文本编码,就是让词语与数字对应起来,建立基于给定文本的词典。(fit方法 )
再根据词典对所有的文本数据进行转码。(transform方法)
scikit库的CountVectorize类就是这种思路。
from sklearn.feature_extraction.text import CountVectorizer
cv = CountVectorizer()
使用fit方法,CountVectorizer()类的会从corpus语料中学习到所有词语,进而构建出text词典。
text=["Hey hey hey lets go get lunch today :)",
"Did you go home?",
"Hey!!! I need a favor"]
text相当于三篇文章
fit学会语料中的所有词语,构建词典
cv.fit(text)
CountVectorizer(analyzer='word', binary=False, decode_error='strict',
dtype=<class 'numpy.int64'>, encoding='utf-8', input='content',
lowercase=True, max_df=1.0, max_features=None, min_df=1,
ngram_range=(1, 1), preprocessor=None, stop_words=None,
strip_accents=None, token_pattern='(?u)\\b\\w\\w+\\b',
tokenizer=None, vocabulary=None)
这里我们查看下“词典”,也就是特征集(11个特征词)
cv.get_feature_names()
Out:
['did',
'favor',
'get',
'go',
'hey',
'home',
'lets',
'lunch',
'need',
'today',
'you']
注意feature_name的返回结果,我们可以发现这几条规律:
一、所有的单词都是小写
二、单词长度小于两个字母的,会被剔除掉,如果我们想要保留长度为1的词 可以使用如cv = CountVectorizer(token_pattern='(?u)\\b\\w+\\b' )
三、标点符号会剔除掉
四、不重复
五、这个特征集是有顺序的
文档-词频矩阵(document-term matrix),英文简写为dtm
dtm=cv.transform(texts)
print(dtm)
Out:
(0, 2) 1
(0, 3) 1
(0, 4) 3
(0, 6) 1
(0, 7) 1
(0, 9) 1
(1, 0) 1
(1, 3) 1
(1, 5) 1
(1, 10) 1
(2, 1) 1
(2, 4) 1
(2, 8) 1
用pandas库以行列形式展示- 在 jupyer notebook中展示的没有加print:
pd.DataFrame(cv_fit.toarray(),columns=cv.get_feature_names())
对应输出的pandas图片,和上面的out(输出)结合来看,就是第0行第3个数为1次,第0行第4个数为1次……
同时在我们pandas显示出来的图片中每一行代表一个文章,每一列代表一个特征,在第0行的hey特征下面的数字为3,表示hey在该文章里面出现了3次。
注意:
此时我们已经构建完成了我们的词频矩阵, 如果我们还想加入新的文档此时我们需要注意了。
举个例子:
new_document = ['Hello girl lets go get a drink tonight']
new_dtm = cv.transform(new_document)
print(new_dtm.toarray())
pd.DataFrame(new_dtm.toarray(), columns=cv.get_feature_names())
Out: new_dtm.toarray()的输出
[[0 0 1 1 0 0 1 0 0 0 0]]
显示如下图:
比如其中,是类别下特征出现的总次数;是类别下所有特征出现的总次数。对应到文本分类里,如果单词word在一篇分类为label1的文档中出现了5次,那么的值会增加5。如果是去除了重复单词的,那么的值会增加1。是特征的数量,在文本分类中就是去重后的所有单词的数量。的取值范围是[0,1],比较常见的是取值为1。
待预测样本中的特征在训练时可能没有出现,如果没有出现,则值为0,如果直接拿来计算该样本属于某个分类的概率,结果都将是0。在分子中加入,在分母中加入可以解决这个问题。
下面的代码来自sklearn的官方示例:
>>> import numpy as np
>>> X = np.random.randint(5, size=(6, 100))
>>> y = np.array([1, 2, 3, 4, 5, 6])
>>> from sklearn.naive_bayes import MultinomialNB
>>> clf = MultinomialNB()
>>> clf.fit(X, y)
MultinomialNB(alpha=1.0, class_prior=None, fit_prior=True)
>>> print(clf.predict(X[2]))
[3]
伯努利模型
在伯努利模型中,每个特征的取值是布尔型的,即true和false,或者1和0。在文本分类中,就是一个特征有没有在一个文档中出现。
还是官网的例子
>>> import numpy as np
>>> X = np.random.randint(2, size=(6, 100))
>>> Y = np.array([1, 2, 3, 4, 4, 5])
>>> from sklearn.naive_bayes import BernoulliNB
>>> clf = BernoulliNB()
>>> clf.fit(X, Y)
BernoulliNB(alpha=1.0, binarize=0.0, class_prior=None, fit_prior=True)
>>> print(clf.predict(X[2]))
[3]
完
以上是关于贝叶斯分类算法的主要内容,如果未能解决你的问题,请参考以下文章