朴素贝叶斯之实践篇
Posted 混沌巡洋舰
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了朴素贝叶斯之实践篇相关的知识，希望对你有一定的参考价值。
在阅读本篇之前，建议先看看 和
拉普拉斯平滑(Laplacian Smoothing)
首先，我们回忆一下我们已经聊过的朴素贝叶斯模型，通过极大化朴素贝叶斯模型对应的对数似然函数，我们得到了下面的朴素贝叶斯模型的参数
这个公式看起来虽然极具对称性和美感，但是，其中有一个潜在的问题。当然，这个问题并不出在我们求解参数的数学上，而在于模型本身隐藏着的一个缺陷。
设想一下，如果在我们所有的训练样本中，第j个特征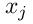 
都没有取等于１这个值，那么，利用上面的公式，我们就可以看到
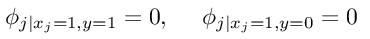
换句话说，在训练样本中，我们从来没有见过第j个特征取值为１的情形，结果，很不幸，在测试集中，存在一个样本，它的第j个特征的取值正好是１，那么，我们就会得到下面的不幸结果
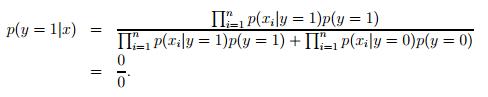
这样的结果当然是我们不希望看到的，因为这会让我们的模型在这种情况下变得手足无措。当然，出现这样的事情，我们是万万不能去责怪我们的模型的。这就像是一个轻量级的拳击手，平时训练的对手体重都在50kg一下，突然，有一天他站上了拳击台，面对的对手是一个体重100kg的对手一般，他从未见过这样强壮的对手，自然就变得手足无措了。
扯了这么久，我们还是没有看到这一大段和我们要将的拉普拉斯平滑有什么关系。接下来，我们当然就要让他俩发生一下关系了。
拉普拉斯平滑是一种避免 0/0 这种不愉快的故事发生的手段。关于拉普拉斯平滑的思想， 我想简单地聊一下我自己的理解，可能不是很准确，大家可以自行判断是否接受。
我们还是看已经提到过的拳击手的例子，为了让他不至于在看到大重量级别的选手时候变得手足无措，最理想的情况下，我们当然希望能够给他找几个重量级的选手来进行训练，但，这显然是不可能的。那我们能怎么办？
办法很土，那就是虽然我是个轻量级选手，也没有重量级的对手来进行训练，那我就自己YY一下各个重量水平的选手的样子，让自己有个心理准备。既然没有真正和他们交过手，那YY的时候当然要不失公平性，换句话说，在训练之前，我们就很天真地认为，不管是哪个重量级的选手，我们都是一样地对待。
下面，我们把这个思想翻译成拉普拉斯平滑，也就是下面的表达式
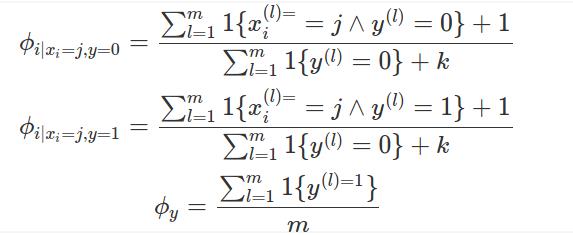
注意到，我们在模型参数的分子上加了１，在分母上加了k。这和我们刚刚的讨论是吻合的。由于我们的每个特征只会取1, 2, ... , k 这k 个值，假设我们没有训练样本，那他们对于的参数值就变成了 1/k, 也就是说，我们对他们进行了同等对待。
值得注意的是，我们没有对先验分布(也就是最后一个式子)进行拉普拉斯平滑处理，当然，如果需要，我们也可以进行同样的处理。
经过拉普拉斯平滑处理，我们发现，0/0 这种不愉快的情形将不会出现了。
文本分类的利器：事件模型(event model)
在这个部分中，我们将聊一聊朴素贝叶斯模型的一种变型，这种变型在处理文本分类中，有很好的效果，例如垃圾邮件识别问题。
现在，我们开始考虑垃圾邮件分类问题。并通过这个问题来介绍朴素贝叶斯模型的简单变种，事件模型。
垃圾邮件分类问题是非常重要的问题，几乎所有的邮箱都内置了垃圾邮件识别的功能，打开邮箱，你会发现，有的邮件自动就被归为了垃圾邮件，这就是因为邮箱中内置了垃圾邮件识别算法。问题的描述其实非常简单，当你收到一封邮件时，算法将通过分析邮件中的词，来判断这封邮件是否是垃圾邮件，如果是垃圾邮件，那么将自动进入垃圾邮箱。
从上面的描述来看，首先，非常明确的一点是，我们面对的是一个二分类问题：对于一封邮件，判断它是垃圾邮件或者不是垃圾邮件。其次，我们会发现，我们面临的是一个文本分析问题，那么，我们所需要构建的特征，自然是要基于文本中的词或者句子的。
首先，我们撇开机器学习不谈，先从直观上来分析一下这个问题，人是怎样分辨一封邮件是否是垃圾邮件的？一般来说，如果我们看到一些关键的词，比如说“大优惠”、“买买买”、“错过这次，你还要再等一年”，我们大概就知道这是一封垃圾邮件了，而且，这样类似的词出现的频率越高，则越有可能是一封垃圾邮件。
基于这样的想法，我们自然地想到通过分析每个词出现的频率来判断邮件的类别，换句话说，也就是把词出现的频率作为特征来进行学习。那么，另一个问题出现了，计算机只能进行数值计算，我们怎样把一封邮件和一个向量进行对应呢？也就是我们怎样统计频率，统计哪些词的频率呢？
为了回答上面的问题，我们需要构造一个字典D，里面按顺序包含着我们所关心的词，这样，我们关系的每个词都对应着一个唯一的位置。这个字典的质量，是非常影响我们识别的准确率的，一些小的构造技巧，将在后面的实验部分进行讨论。
现在，我们就要开始聊事件模型了。引入事件模型的一个动机，是为了解决文本本身长短不一的问题。比如说，“买”这个词在一封只有100个词的邮件中出现了五次，和在一封1000个词的邮件中出现了五次相比，前者更有可能是一封垃圾邮件。而在之前的朴素贝叶斯模型中，我们可以看到，模型参数表达式的分母只和训练样本的个数有关(也就是只和有多少封邮件有关)，不能很好地反应我们刚刚提到的这一点。因此，我们开始考虑下面的模型：
对于一封邮件，因为我们已经建好了一个字典，假设字典中一共用V个词，那么，对于邮件中的任何一个词，如果它出现在字典中(我们关心的词)，那他就对应了1, 2, ..., V 这V个整数中的唯一一个数。那么，对于第i个训练样本，如果其一共有ni 个词，那么，它就唯一地对应到了一个向量
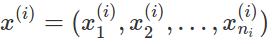
其中，每个分量的取值都是1, 2, ..., V 中的某一个整数。假设 y = 0 表示邮件不是垃圾邮件，y = 1 表示邮件是垃圾邮件。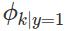
表示邮件是垃圾邮件，且字典D中的第k个词在邮件中某个位置上出现的概率，
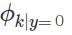表示邮件不是垃圾邮件，且字典D中的第k个词在邮件中某个位置上出现的概率，
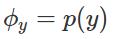表示y的概率分布(先验概率分布)。于是，和朴素贝叶斯模型类似，对于 m 个训练样本，我们可以写出事件模型的似然函数
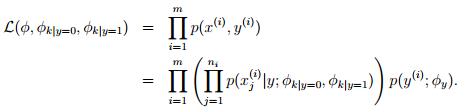
通过极大化其对应的对数似然函数，我们得到了如下的模型参数
类似地，我们通过拉普拉斯平滑，得到下面的模型参数估计
在下面的部分，我们将看到事件模型在垃圾邮件分类问题上的具体表现。
Talking is cheap, show me the code!!!
取这个标题并不是为了炫耀一下英语，只是引用一下在机器学习这个圈里流传地比较广的一句话，来表明我决定 show 一些代码，算是一个小福利了。对了，上面这句话翻译成中文我个人觉得有个直接了当的说法：别只光说不练！！！这个也是我自己觉得在机器学习中非常中肯的建议，不要每天只带着涨姿势的心态看看这个模型，看看那个模型，然后感慨一番，真正的开始，是自己写点代码实现一些你觉得有趣的模型，看看它的表现到底怎么样。
上面这段稍微有点跑题了，下面进入正题。
现在，我通过Andrew Ng 在 CS229 Machine Learning 这门课程中提供的一个垃圾邮件分类的数据集，向大家展示事件模型在真实的垃圾邮件分类中的能力。
在这个数据集中，一共有６个不同的训练数据集，分布包含着不同个数的训练样本，同时，包含着一个测试集。关于这个数据集的结构，我想稍微讲一讲，这样，方便大家理解代码。(下面蓝色这段关于数据集的描述比较无聊，不感兴趣的读者可以跳过)
每个数据集的第一行是这个数据集的名字，没有实际的意义。第二行中有两个整数，分别表示包含的训练样本(或者测试样本)的个数和字典中包含的词的个数。然后，紧接着的一行是所有字典中的词的列表。接下来就是数据集的正题了，每一行(由换行符'\n'表示一行结束，不是眼睛看上去的一行)表示一个训练样本，数据集采用所谓"cumsum"的格式，奇数位置的数表示相对上一个词在字典中位置的偏移量，紧接着的偶数位置的数字表示这个词出现的次数。
跳过上面蓝色部分的读者只要知道代码中 read_data 这个函数是用来从数据集中读取数据就好了。作为机器学习中最常用的编程语言之一，以后我贴出的代码尽量用 python 写。注意，我个人目前还是用 python 2.7 比较多，如果有用python 3 的读者，可能要稍微修改一下代码。
我发现直接把代码贴出来在手机上阅读体验很差，我把代码和数据都上传到百度网盘了，大家可以通过文末提供的链接和提取码获取。
下面展示一下实验结果。
训练样本为50封邮件：测试正确率：96.125%
训练样本为100封邮件：测试正确率：97.375%
训练样本为400封邮件：测试正确率：98.125%
训练样本为1400封邮件：测试正确率：98.375
我们可以发现，事件模型在垃圾邮件分类问题中表现地相当不错。下面，我们来聊一点细节。
在实际应用中，字典的构造非常的重要。通常来说，我们要避免在字典中包含一些出现频率比较高，但是对于分类意义不大的词，例如中文中的“我”， “你好”， 英文中的 "the", "a" 这类词。应该尽量选择一些在日常生活中使用频率适中的词。
训练模型，计算模型参数，已及通过贝叶斯模型计算后验概率 p(y|x)时 一定要取对数。一个原因是训练时，通过取对数能将乘积变成求和，另一个很重要的原因是计算精度的问题。要知道，把很多小于１的数乘在一起得到的数可能非常的接近零，用这样的数做分母是非常危险的！！！
看到这里，估计大家也看累了。贝叶斯思想在机器学习中非常非常重要，绝不是简单的一两个杂谈就能聊清楚的。对于朴素贝叶斯模型，我们暂时只聊这么多，但是贝叶斯思想，在我们以后的推送中可能会经常聊起。
最后，提一句，不知道有多少读者会读到这一句，事实上，在一类线性回归问题中我们可以看到，利用贝叶斯模型，实际上相当于正则化的 disrimitive 学习模型，这一点，以后有机会的话我可能会详细地聊一聊。
祝大家周末愉快！！！
数据与代码链接：https://pan.baidu.com/s/1pLCTYe3
提取码： aff6
版权声明：数据集与代码仅用于交流学习！！！
以上是关于朴素贝叶斯之实践篇的主要内容，如果未能解决你的问题，请参考以下文章