Python之朴素贝叶斯对展会数据分类
Posted 老胡的储物柜
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Python之朴素贝叶斯对展会数据分类相关的知识,希望对你有一定的参考价值。
读大学时期写的博文
目的
国内数据比较少,占四百多条,在类别上来看有所属行业这一列,所以比较好处理,国外数据就有些尴尬:

国外网站展会数据将近五万多条,跟分类有关的只有 categories这一列数据,都是一些标签词,还偏少。
现在需要将五万多条展会数据进行分类,如何解决这个问题,我觉得可以写个朴素贝叶斯分类器。
数据
朴素贝叶斯分类器是利用样本数据来进行训练的,每个样本必须含有一组特征词以及对应的分类。
数据的准备
获取的国内数据就很适合作为训练数据,可以将其处理成如下格式作为样本输入:

训练数据主要是这两列,所属行业以及展会范围,每一行的类别都有其对应的展会范围,将这些作为训练数据实在再好不过,我们将其称之为训练集。
那么相对应,国外待分类的展会数据便是测试集。
我们将利用训练好的分类器,将测试集一一输入,看看能否得到期望的输出结果。
可是现在有个问题,作为训练集的国内数据只有四百多条,实在太少,于是我只能再去那个国内展会网站将以前的展会数据尽量爬取下来,最终训练集达到了 39555条,虽说数量还是不够,但是不试试最终分类器的分类结果,说不定准确率还可以呢?
分词&&提取
不积小流,无以成江海,以小见大,咱们看这样一条数据:
所属行业:建材五金
展会范围:各类卫生洁具、浴室家具和配件、面盆、马桶、淋浴房、浴缸、花洒、水龙头及配件、浴室照明、镜子、五金挂件等
思考一下,这一条数据的所属行业和展会范围有什么关系,我们将从这里得到编写分类器的出发点。
在这条数据中,展会范围的内容是具有一定的代表性的,其代表这条数据的描述很偏向建材五金这个行业。
那我么是不是可以提炼出这个描述的关键词,从而让这个关键词代表建材五金这个行业。
# 可以利用结巴分词
import jieba.analyse
con = "各类卫生洁具、浴室家具和配件、面盆、马桶、淋浴房、浴缸、花洒、水龙头及配件、浴室照明、镜子、五金挂件等"
feature = jieba.analyse.extract_tags(con, 8)
print(feature)
# output:['配件', '各类', '家具', '五金', '照明', '浴室', '淋浴房', '浴缸']
那么刚刚那条数据可以这样看:
# data_01
所属行业:建材五金
描述关键词:'配件', '各类', '家具', '五金', '照明', '浴室', '淋浴房', '浴缸'
以此类推,如果一条未分类数据的关键词也是这样,那是不是可以将该数据归为建材五金这个类别,是的,你可以这么干。
但有个问题,若该未分类数据的关键词只含有以上关键词的某个,比如:
# data_02
所属行业:未知
描述关键词:'配件','家具'
这样子若分为建材五金不大对吧,我倒觉得应该分为房产家居,这个问题可以解决,就让我们的概率出场吧。
大三的时候学过概率统计,也记得一个公式名为贝叶斯定理。
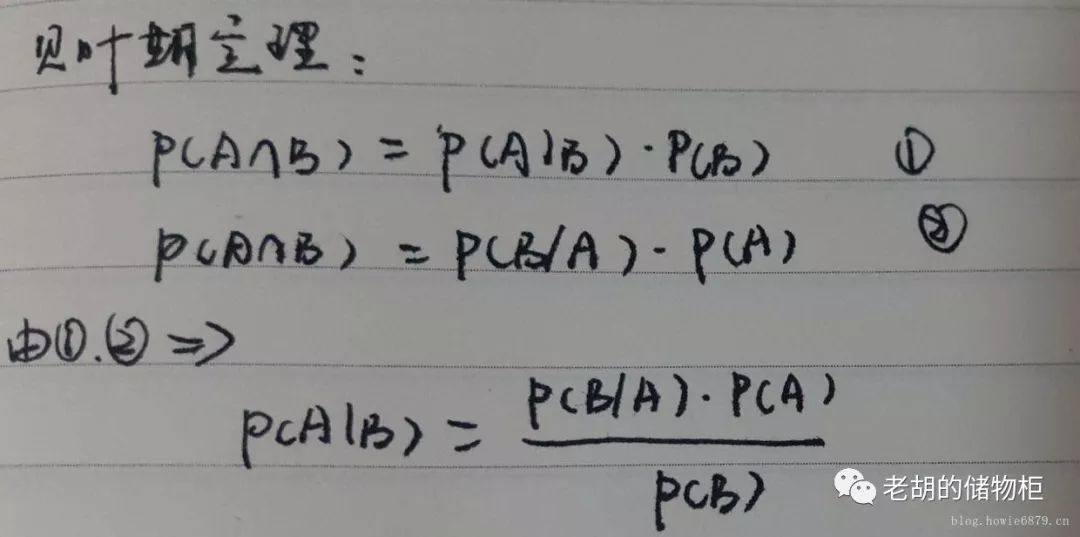
这表示计算条件概率的公式:
P(A\B) = P(B\A)*P(A)/P(B) == 后验概率 = 先验概率 x 调整因子
# 这样写会不会更加清晰
P(category\keywords) = P(category) * P(keywords\category)/ P(keywords)
## 朴素贝叶斯便是假设即将被组合的各个概率是独立的,可以理解成keyword1出现在category1的概率和keyword2出现在category1的概率是没有关系的,是独立的。
P(category\keywords) = P(category) * P(keyword1\category)P(keyword2\category)...P(keywordn\category)/ P(keywords)
总结就是,我们先求出样本空间中每个分类的概率P(category)——先验概率
再求出一组待分类数据的关键词在各个类别中的概率P(keywords\category)——调整因子
最后先验概率 * 调整因子得出后验概率,再经过比较,后验概率最大的,便是待分类数据最可能的类别。
我们的准备很充足了,但在写分类器之前,还是先将下面要用到的数据提前提取出来。
2.2.1.确定训练数据有多少类别
2.2.2.训练数据的关键词集合,为了方便后续计算,将其转为id:word的格式存为id_word.txt

2.2.3.计算出每个关键词在每个不同类别出现的概率,将其转为category=id:pro(id)的格式存为tf_id_word.txt

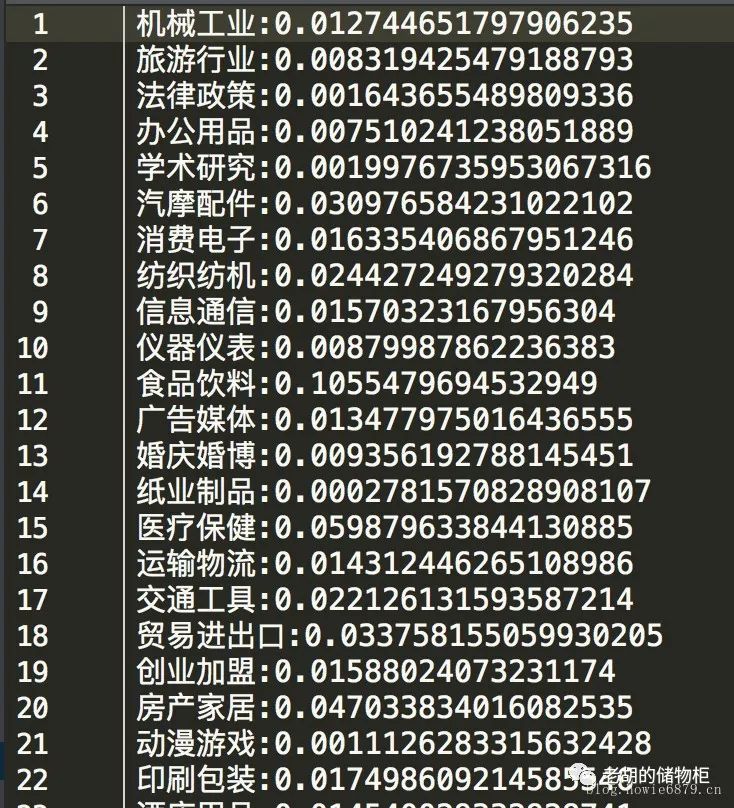
2.2.4.求出样本空间中每个分类的概率P(category)——先验概率,将其转为category:pro(category)的格式存为type_pro.txt
编码
经过前面的步骤,现在编写代码实在简单,不过有两点要注意。
其一是关键词并不是在每个类别都会出现,这样会导致P(keyword\category) = 0,进而导致整个后验概率为0,为了解决这个问题,可以引入拉普拉斯平滑,这样便确保不会出现为0的情况,具体代码中有介绍。
其二是若每个调整因子的数值都很小,大家都知道很小的值相乘,会导致结果变得更小,这样子表现出各个分类结果的后验概率便会出现问题,这个问题便是下溢出问题,解决办法便是将其转化为对数,对数相乘便是对数相加,这样便很巧妙的解决了这个问题。
好了,直接上代码,让我们看看分类的结果吧。
# -*-coding:utf-8-*-
__author__ = 'howie'
import jieba.analyse
import pandas as pd
import math
class Pridict(object):
"""
利用txt/中数据进行朴素贝叶斯算法训练
"""
def __init__(self):
# 初始化结果字典
self.resultData = {}
def getKeyword(self, path):
"""
通过结巴分词进行关键词提取
:param path: 待分词文件路径 相关参数可更改 也可不调用直接写
:return: keywordDic = {index:['word1','word2'...]}
"""
keywordDic = {}
df = pd.read_csv(path)
for des in df.values:
jieba.analyse.set_idf_path('txt/type_dict.txt')
feature = jieba.analyse.extract_tags(des[15], 8)
keywordDic[des[16]] = feature
return keywordDic
def idDic(self, keywordDic):
"""
将每条待分类关键词替换成对应的单词向量
:param keywordDic:格式 keywordDic = {index:['word1','word2'...]}
:return: keywordDic = {'1': ['12198', '16311', '6253', '8302']}
"""
with open('txt/id_word.txt', 'r', encoding='utf8') as of:
lines = of.read().split('\n')
for key, values in keywordDic.items():
id_word = []
for eachValue in values:
id_word += [eachLine.split(':')[0] for eachLine in lines if eachValue == eachLine.split(':')[-1]]
keywordDic[key] = id_word
return keywordDic
def calPro(self, keywordDic):
"""
计算每一组待分类数据关键词对应概率总和
:param keywordDic:格式 keywordDic = {'1': ['12198', '16311', '6253', '8302']}
:return: result = {'1': {'type1': -33.23204707236557, 'type3': -31.376043125934267, 'type3': -27.385192803356617...}
"""
result = {}
# print(keywordDic)
# 获取每个类别关键词出现概率
with open('txt/tf_id_word.txt', 'r', encoding='utf8') as of:
lines = of.read().split('\n')[0:-1]
# 循环待分类数据
for key, values in keywordDic.items():
result[key] = {}
# 读取分类概率文件中读取每行数据
for eachLine in lines:
valLen = len(values)
valPro = list(map(lambda x: '', [x for x in range(0, valLen)]))
laplace = ''
# 分类名称 该分类下关键词概率
lineData = eachLine.split("=")
# 该分类下每个关键词概率
eachLineData = lineData[-1].split("#")
# 循环每个待分类字典的关键字向量
for index,eachValue in enumerate(values):
# 每个关键词对应的词向量以及词概率 得到所有关键词该分类下的概率列表
resPro = [eachPro.split(':')[1] for eachPro in eachLineData if eachValue == eachPro.split(':')[0]]
# 防止待分类关键词概率为0,添加拉普拉斯平滑
laplace = str(1 / (valLen + len(eachLineData)))
valPro[index] = (resPro[0] if resPro else laplace)
valPrlLen = int(valLen / 2)
# 处理关键词为空 增加限制条件,排除小概率分类影响后验概率大小
if valPro:
if valPro.count(laplace) <= valPrlLen:
# 防止下溢出转化为对数相加
typePro = sum([math.log(float(x)) for x in valPro])
result[key][lineData[0]] = typePro
else:
# 将该待分类数据标记为None
result[key] = None
return result
def resPro(self, result):
"""
为各个分类乘上先验概率 提高分类成功率
:param result: 格式 result = {'1': {'type1': -33.23204707236557, 'type3': -31.376043125934267, 'type3': -27.385192803356617...}
:return: resultData = {'1': {'type': -28.135469210164924}}
"""
for eachKey, eachVal in result.items():
# 初始化每个待分类数据字典 储存最可能分类的概率
self.resultData[eachKey] = {}
# 初始化最终分类结果概率
allPro = {}
if eachVal:
# print(eachVal)
with open('txt/type_pro.txt', 'r', encoding='utf8') as of:
lines = of.read().split('\n')
for line in lines:
lineData = line.split(':')
# 乘上该分类概率 即先验概率
allPro = dict(allPro,**{key:(value + math.log(float(lineData[1]))) for key, value in eachVal.items() if key == lineData[0]})
# 返回各个分类对应后验概率最大值
largest = max(zip(allPro.values(),allPro.keys()))
self.resultData[eachKey][largest[1]] = largest[0]
else:
# 无法分类
self.resultData[eachKey] = {'failed': None}
return self.resultData
def mainPri(keywordDic):
pri = Pridict()
dic = pri.idDic(keywordDic)
result = pri.calPro(dic)
resultData = pri.resPro(result)
return resultData
初步写好分类器,其实这才是任务的开始,分类器的最重要的是第二部分的数据提取,接下来需要通过不断地训练,让数据变得更加优雅美丽,从而让分类器的结果趋于完美,本人苦逼地调了一个星期,现在也就勉强能用。
让我们看看分类器的分类效果:
可以看到分类器给出的参考分类很有代表性,这一段就此结束,若有错误,敬请指出,谢谢。
往期推荐:
以上是关于Python之朴素贝叶斯对展会数据分类的主要内容,如果未能解决你的问题,请参考以下文章