朴素贝叶斯：世界上最广泛的分类模型之一，看完我马上就去了福利彩票店！

Posted 2021-04-25 裸露奇点

贝叶斯的简介

贝叶斯(Thomas Bayes,1702—1761)英国牧师、业余数学家。生活在18世纪的贝叶斯生前是位受人尊敬英格兰长老会牧师。为了证明上帝的存在，他发明了概率统计学原理，遗憾的是，他的这一美好愿望至死也未能实现。贝叶斯在数学方面主要研究概率论。他首先将归纳推理法用于概率论基础理论，并创立了贝叶斯统计理论，对于统计决策函数、统计推断、统计的估算等做出了贡献。1763年发表了这方面的论著，对于现代概率论和数理统计都有很重要的作用。贝叶斯的另一著作《机会的学说概论》发表于1758年。

贝叶斯所采用的许多术语被沿用至今。贝叶斯思想和方法对概率统计的发展产生了深远的影响。今天，贝叶斯思想和方法在许多领域都获得了广泛的应用。从二十世纪20~30年代开始，概率统计学出现了“频率学派”和“贝叶斯学派”的争论，至今，两派的恩恩怨怨仍在继续。

内容简介

本文叙述朴素贝叶斯法，包括朴素贝叶斯法的学习与分类，朴素贝叶斯法的参数估计算法。（阅读本文大概只需6分钟）

朴素贝叶斯（naÏve Bayes）法是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的数据集，首先基于特征条件独立假设学习输入/输出的联合概率分布；然后基于此模型，对给定的输入x，利用贝叶斯定理求出后验概率最大的输出y。朴素贝叶斯法实现简单，学习与预测的效率都非常高，是一种常用的方法。

朴素贝叶斯法的学习与分类

基本方法

设输入空间为n维向量的集合，输出空间为类标记集合{c1,c2,...,ck}。输入为特征向量x，输出类标记（class label）y。X是定义在输入空间上的随机向量，Y是定义在输出空间上的随机变量。P(X,Y)是X和Y的联合概率分布，训练数据集

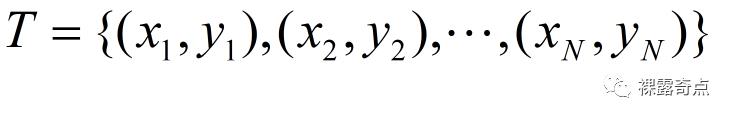
由P(X，Y)独立同分布产生。

朴素贝叶斯法通过训练数据集学习联合概率分布P(X,Y)。具体的，学习以下先验概率分布及条件概率分布。先验概率分布

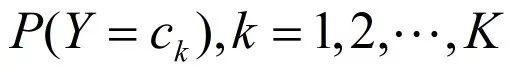
条件概率分布

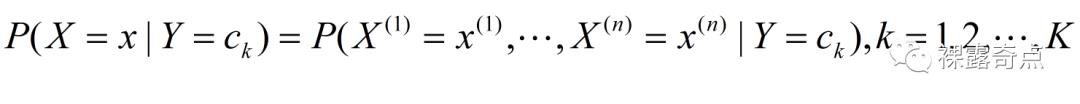
于是学习到联合概率分布P(X,Y)。

条件概率分布P(X=x|Y=c(k))有指数级数量的参数，其估计实际是不可行的。事实上，假设x[j]可取值有S(j)个，j=1,2,...,n，Y的可取值有K个，那么参数个数为K∏S(j)。(注：部分数学符号无法输入，其中[]表示为上标，()表示为下标)

朴素贝叶斯法对条件概率分布做了条件独立性的假设。由于这是一个较强的假设，朴素贝叶斯法也由此得名。具体地，条件独立假设是

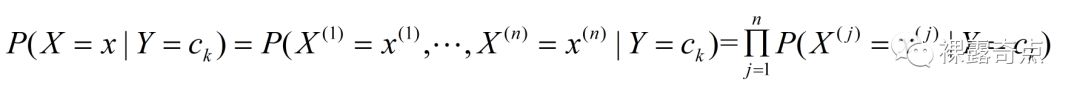
朴素贝叶斯法实际上学习到生成数据的机制，所以属于生成模型。条件独立假设等于是说用于分类的特征在类确定的条件下都是条件独立的。这一假设使朴素贝叶斯法变得简单，但有时会牺牲一定的分类准确率。

朴素贝叶斯法分类时，对给定的输入x，通过学习到的模型再计算后验概率分布P(Y=c(k)|X=x)，将后验概率最大的类输出。后验概率计算根据贝叶斯定理进行计算

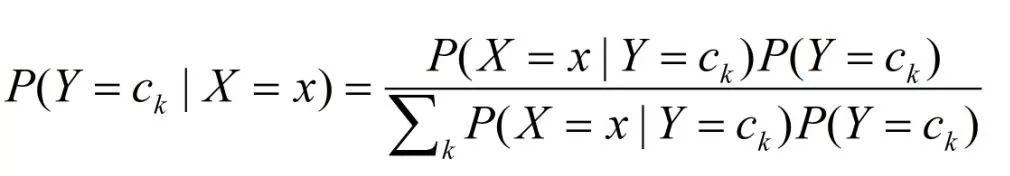
将条件独立假设等式带入有

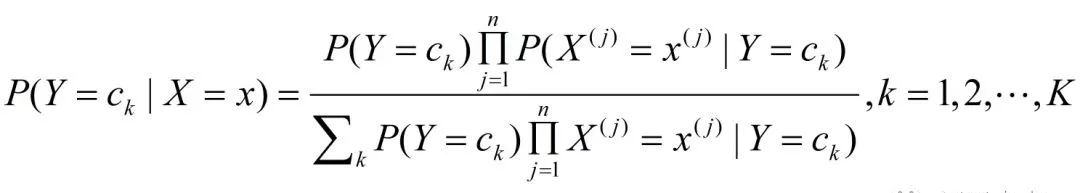
这是朴素贝叶斯分类的基本公式。于是，朴素贝叶斯分类器可表示为

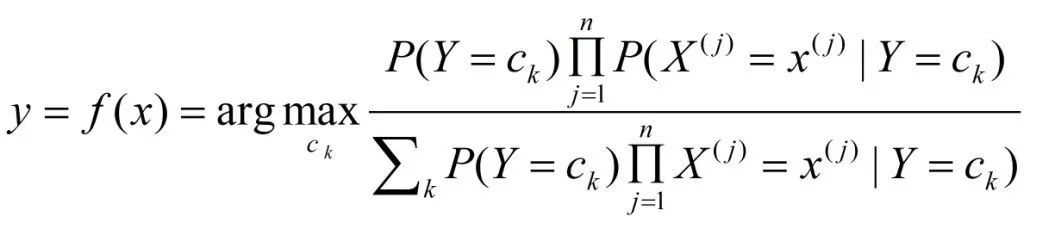
注意到，在上述式子中分母对所有出c(k)都是相同的，所以

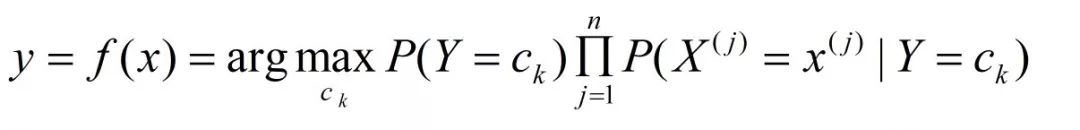
后验概率最大化的含义

朴素贝叶斯法将实例分到后验概率最大的类中，则等价于期望风险最小化。假设选择0-1损失函数

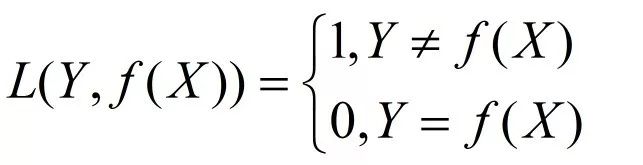
式中f(X)是分类决策函数。这时，期望风险函数为R(f)=E[L(Y,f(X))]，期望是对联合分布P(X,Y)取的。由此取条件期望

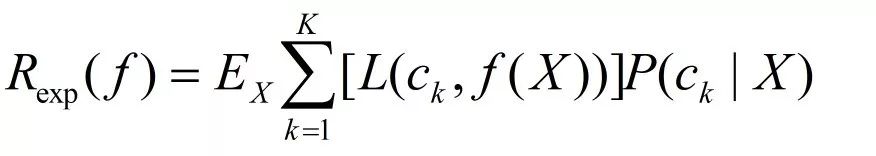
为了使期望风险最小化，只需对X=x逐个极小化，由此得到：

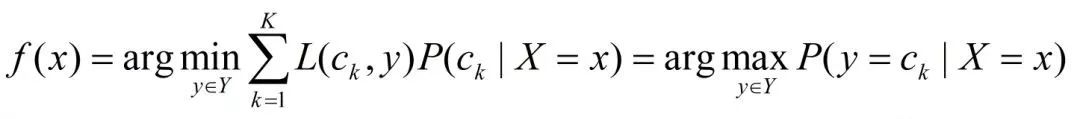
这样一来，根据期望风险最小化准则就得到了后验概率最大化准则

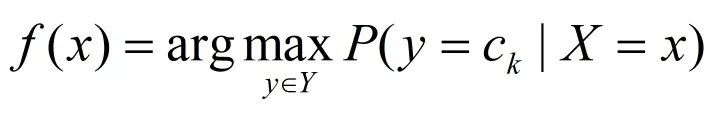
即朴素贝叶斯法所采用的的原理。

朴素贝叶斯法的参数估计

极大似然估计

在朴素贝叶斯中，学习意味着估计P(Y=c(k))和P(X=x[j]=|Y=c(k))。可以应用极大似然估计法估计相应的概率。先验概率P(Y=c(k))的极大似然估计是

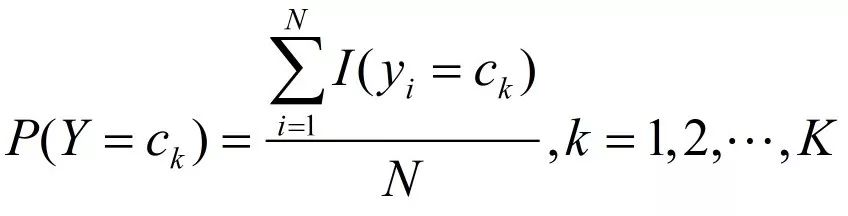
设第j个特征x[j]可能的取值集合为{a(j1),a(j2),......a(js)}，条件概率P(X[j]=a(jl))|Y=c[k]）的极大似然估计是

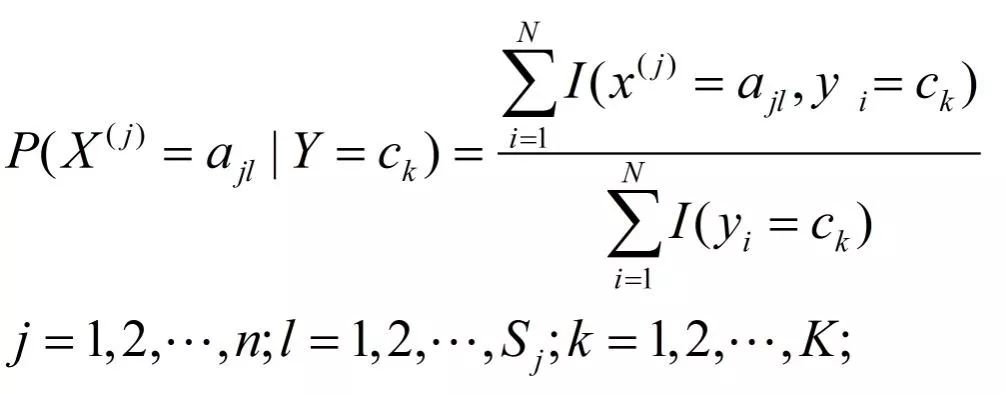
式中，xi[j]是第i个样本的第j个特征；ajl是第j个特征可能取值的第l个值；I为指示函数。

学习与分类算法

下面给出朴素贝叶斯法的学习与分类算法

贝叶斯估计

用极大似然估计可能会出现所要估计的概率值为0的情况。这时会影响到后验概率的计算结果，使分类产生偏差。解决这一问题的方法是采用贝叶斯估计。具体地，条件概率的贝叶斯估计是

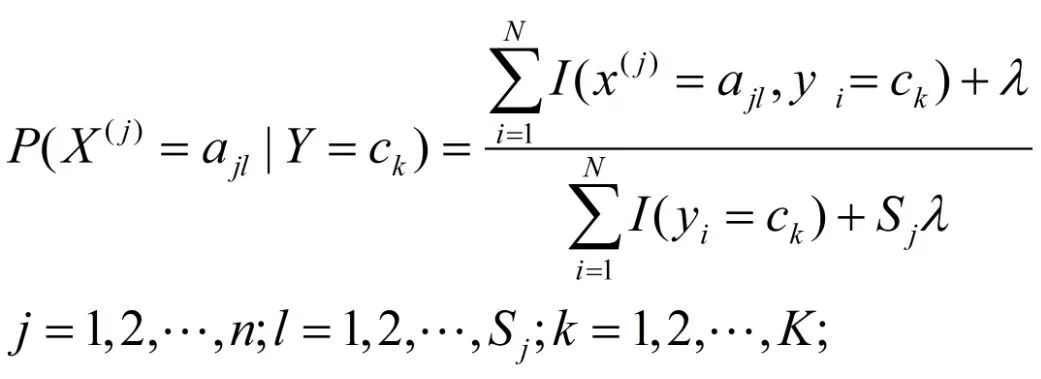
式中的λ≥0。等价于在随机变量各个取值的频数上赋予一个正数λ。当λ=0时就是极大似然估计。常取λ=1，这是称为拉普拉斯平滑(Laplace smoothing)。显然，对于任何的L和K，都不会出现为0的情况，上述式确实是一种概率分布。同样，先验概率的贝叶斯估计是

总结

朴素贝叶斯法的基本假设是条件独立性，这是一个较强的假设。由于这一假设，模型包含的条件概率的数量大为减少，朴素贝叶斯的学习与预测大为简化。因而，朴素贝叶斯法高效，且易于实现。其缺点是分类的性能不一定很高。如果假设输入变量之间存在概率依存关系，这时模型就变成了贝叶斯网络。