分类算法之——KNN朴素贝叶斯
Posted 小小新说数据
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了分类算法之——KNN朴素贝叶斯相关的知识,希望对你有一定的参考价值。
“ 分类问题属于机器学习中的监督学习方法,它主要解决的问题是:被告知数据集的标签之后,将数据集中的样本与标签进行匹配从而训练出一个函数,当新的数据到来时,可根据学到的函数对新数据进行分类。接下来将介绍两种常见的分类方法。”
01
—
KNN
KNN算法也叫K—最近邻算法,其基本思想是:若某样本在特征空间中与其相邻的k个样本大多数属于某一个类别,则该样本也属于这个类别,与“近朱者赤,近墨者黑”一个道理。如图1所示,与待测样本距离最近的6各点中,类别为1的最多,将待测样本的类别标为1.显而易见,KNN中所选择的邻居都是已经正确分类的样本。
图1:KNN算法示例图
KNN的基本步骤如下:
1:计算待分类样本与各训练集数据之间的距离
2:对距离进行排序
3:选取距离最小的k个样本
4:计算k个样本的类别出现的频率
5:将k个样本中出现频率最高的类别作为待测样本的类别
那么问题来了,怎么确定k的值和怎么计算各样本之间的距离呢?
k的值:交叉验证法,从K=1开始,逐个计算预测准确率,取准确率最高时的K值。K值一般低于训练样本数的平方根。
各样本之间的距离:可由距离计算方式和相似性度量方式计算出,以下介绍几种常见的相似性度量方法:
设有向量:
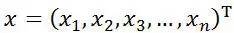
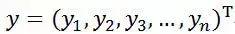
则它们距离的计算方式:
L1范式(曼哈顿距离)
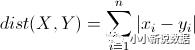
L2范式(欧式距离)
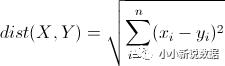
切比雪夫距离
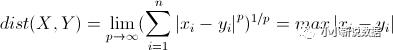
以上距离方法值越小,越相似。
接下来介绍相似性度量方法:
皮尔逊相关系数
即相关分析中的相关系数r,分别对X和Y基于自身总体标准化后计算空间向量的余弦夹角。
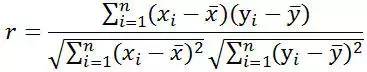
向量空间余弦夹角相似度
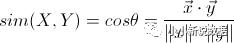
Jaccard相似度
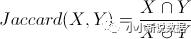
KNN算法优点:
1. 简单,无需训练,无需参数估计;
2. 适合对稀有事件进行分类;
3. 对多分类问题结果更好,比SVM要好些。
KNN算法缺点:
1. 对测试样本分类需全遍历,计算量大;
2. 当正负样本不平衡时,如一个类的样本量很大,而其他类样本量很小时,待测样本K个邻居中大样本量的类别中的样本占多数,导致分类错误。
02
—
朴素贝叶斯
朴素贝叶斯算法以贝叶斯定理为基础,而“朴素”是因为该算法以各特征之间相互独立为前提。其分类的基本思想是对于待分类的数据,求出该数据属于某类别的概率,以最大概率对应的类别作为它的标签。
贝叶斯公式:
转换为问题中的场景:
我们只需要根据上面的公式算出p(类别|特征)就可以了。
以下为朴素贝叶斯算法过程:
1):对于待分类x={a1,a2,...an}其中a为x的属性
2):有类别集合c = (c1,c2,....,cm)
3):计算p(c1|x).....p(cm|x),并取其中最大值确定x的类别
在步骤3中,每一个p(ci|x),p(ci|x)= p(x|ci)p(ci)/p(x) 在集合中p(x)都是确定的,因此我们只需要关注分子就可以了。由于每个特征是相互独立的,p(x|ci)p(ci) = p(a1|ci)p(a2|ci)...p(an|ci)*p(ci) 其中p(ci)可由训练集中类别ci出现的概率确定。
那么p(a1|ci)怎么求出呢?这需要根据x的分布来确定,常见的贝叶斯模型的分布有:
高斯分布型:用于classification问题,假定属性/特征服从正态分布的。
多项式型:用于离散值模型里。比如文本分类问题里面我们提到过,我们不光看词语是否在文本中出现,也得看出现次数。如果总词数为n,出现词数为m的话,有点像掷骰子n次出现m次这个词的场景。
伯努利型:最后得到的特征只有0(没出现)和1(出现过)。
最后,总结朴素贝叶斯的优缺点如下:
优点:
(1) 算法逻辑简单,易于实现(算法思路很简单,只要使用贝叶斯公式转化即可!)
(2)分类过程中时空开销小(假设特征相互独立,只会涉及到二维存储)
缺点:
朴素贝叶斯假设属性之间相互独立,这种假设在实际过程中往往是不成立的。在属性之间相关性越大,分类误差也就越大。
以上是关于分类算法之——KNN朴素贝叶斯的主要内容,如果未能解决你的问题,请参考以下文章