BAT面试题11：为什么朴素贝叶斯如此“朴素”？

Posted 2021-04-25 Python与算法社区

公号下周会连续送出三期实在福利

11 为什么朴素贝叶斯如此“朴素”？

朴素贝叶斯模型，全称为：Naive Bayesian Model，Naive 能翻译为朴素，已经是很高看它了，因为我们知道naive的含义如下：

naive: marked by or showing unaffected simplicity and lack of guile or worldly experience;

它是简单的，它是缺乏worldly experience的。

正如它的名字一样，朴素贝叶斯模型假设样本特征彼此独立，没有相关关系。正如我们所知，这个假设在现实世界中是很不真实的，因此，说朴素贝叶斯真的很“朴素”。

但，朴素贝叶斯模型就没用了吗？ 不是的。这个假设现实中基本上不存在, 但特征相关性很小的实际问题还是很多的, 所以这个模型仍然能够工作得很好。

---

下面是朴素贝叶斯的例子解释。

假如我是一个质检员，现在接到了三箱零件需要检验，其中第一箱有10个零件，第二箱有20个零件，第三箱有15个。半小时过去了，检验的结果出炉，第一箱有1个不合格，第二箱有3个不合格，第三箱2个不合格。

下午领导要来视察了，看看我验的货到底有没有问题，于是他随手拿了一个零件，我心里默默计算，领导拿到这个件为合格件的概率有多大？

在这个问题中，领导拿的这个零件首先一定在这3个箱子中的某一个，因此样本空间可以由这3个箱子组成，记 Ai 为从第i个箱子拿的零件，i的取值范围为1,2,3。然后再用一个事件来标记拿到正品，记为B，因此，领导拿到这个件为合格件的概率，记为 P(B)。

那么这个P(B)等于多少呢？这个事件B的发生肯定来自于样本空间吧，也就是说这个合格件要么从A1，A2，或者A3中获取到，因此，

1 P(B) = P(A1)*P(B | A1) + P(A2) *P(B | A2) + P(A3)*P(B | A3)
2
3       = (1/3) * 9/10 + (1/3) * 17/20 + (1/3) * 13/15 
4
5       =  0.872

上面P(B | A1) 是条件概率：零件来自于第一个箱子的条件下，并且它为合格件的概率。

果不其然，领导抽到了一个合格品，然后他亲自检验了下，发现质检的没有问题，冲着我笑了笑，很满意地拍拍屁股就走人了。

当他走了的时候，我想到了一个问题，领导抽的这个合格品来自于箱子1的概率是多大呢？这个问题也就是求 P(A1 | B)，即取到合格品事件B发生了地情况下，来自于A1的概率。

求P(A1 | B)称为求解逆向概率，这个概率往往是不好求解答，但是它对应的正向概率：P(B | A1)，往往求解简单。

因此，自然地，既然 P(A1|B)比较难求解，我们如下转化一下：

1P(A1| B) =  P(A1*B) / P(B) 

其中，A1*B 事件表示从第一个箱子抽取且为合格件，则

1 P(A1*B) = P(A1) * P(B | A1) = (1/3) * 9/10 =  0.3 

P(A1*B)，也可以记为：P(A1,B)，它称为联合概率。

因此，

1P(A1| B) =  0.3  / 0.872 = 0.344 

这个已知B发生，然后，预测B来自于哪里，便是贝叶斯公式做的事情。

那么这个例子如何上升进而提取出一个模型出来呢？

2 例子引出贝叶斯公式

以上《合格品的例子》的样本空间有 A1，A2 ，A3 组成，它们把样本空间划分为三部分。

如果将划分上升到由 n 个部分组成，抽中一个合格件为本次随机试验的事件B，明显地，P(Ai) 和 P(B)都大于零，则事件B发生后，找出它属于哪个类别的计算公式如下：

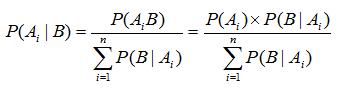
贝叶斯公式是要找出组成发生事件B的各个样本空间，然后预测事件B的发生来自于Ai的概率。

其中 P(Ai) 称为原因的先验概率，可以看到它是在不知道事件B是否发生的情况下获取的概率。比如在抽取零件时，我们不知道能不能抽取到合格件，但是选择任意一个箱子的概率一定都为1/3，所以称为先验概率。

而 P(Ai | B) 是原因的后验概率，它是在知道了事件B发生的条件下，有了这个进一步的信息后，判断原因 Ai 发生的概率有多大。可以看到，一般地，如果对样本空间做了大于1的划分，即：

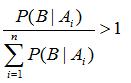
所以根据上面提到贝叶斯公式，不难推断出：

这也就是说在获取了进一步的信息B后，原因的后验概率一般大于原因的先验概率。

朴素贝叶斯的应用实战：

公号下周会连续送出三期实在福利

点赞转发=最大支持=坚持