朴素贝叶斯算法原理

Posted 2021-04-25 数据私房菜

摘要：本文介绍了贝叶斯公式，并根据公式而产生的朴素贝叶斯分类算法在机器学习中的应用，并列举了朴素贝叶斯分类算法的优缺点。

    

1贝叶斯公式的理解

贝叶斯定理（Bayes' theorem）是概率论中的一个定理，它跟随机变量的条件概率以及边缘概率分布有关。在有些关于概率的解说中，贝叶斯定理能够告知我们如何利用新证据修改已有的看法。通常事件A在事件B发生的条件下的概率，与事件B在事件A发生的条件下的概率是不一样的；然而这两种是有确定关系的，这种关系就是贝叶斯定理，我们忽略推导关系，直说最终的结论。

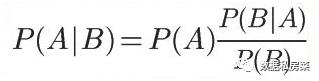
从公式来看，我们需要知道这么3个事情：

1）先验概率

我们把P(A)称为"先验概率"（Prior probability），即在不知道B事件发生的前提下，我们对A事件发生概率的一个主观判断。

2）可能性函数

P(B|A)/P(B)称为"可能性函数"（Likelyhood），这是一个调整因子，即新信息事件B的发生调整，作用是，使得先验概率更接近真实概率。可能性函数你可以理解为新信息过来后，对先验概率的一个调整。
如果"可能性函数"P(B|A)/P(B)>1，意味着"先验概率"被增强，事件A的发生的可能性变大；
如果"可能性函数"=1，意味着B事件无助于判断事件A的可能性；
如果"可能性函数"<1，意味着"先验概率"被削弱，事件A的可能性变小。

3）后验概率

P(A|B)称为"后验概率"（Posterior probability），即在B事件发生之后，我们对A事件概率的重新评估。

所以，贝叶斯定理：  后验概率=先验概率*可能性函数

我们用个经典例子说明贝叶斯定理，有两个一模一样的碗，

碗A里面放着3个白球，一个红球。ＯＯＯＯ

碗B里面红色白色球各两个。ＯＯＯＯ

我们现在从随机一个碗中拿出一个随机的球，发现是白色的球，请问从哪个碗拿出的概率更大？我们不用计算，凭直觉也知道是碗A，但事实是如此吗?

 

我们用贝叶斯定理计算一下：

由于两个碗是一样的，所以P(A)=P(B),也就是说在球被取出之前，两个碗被选中的概率是相同，P(A)=0.5,这个概率我们就叫做先验概率。

假设W为取出白色球事件， 我们最终问题就是已知W的情况下，来自碗A的概率，即求P(A|W),这个就是后验概率，即W事件发生后，对P(A)的修正。

已知从A碗取出白球的概率，即P(W|A)=0.75，

从全部球中取出白色求的概率P(W)=5/8=0.625  

根据公式：

P(A|W)=P(W|A)P(A)/p(W)=0.75*0.5/0.625=0.6

贝叶斯定理证明了我们的猜测，拿出白球后，A事件得到了增强。

2朴素贝叶斯分类原理

我们在大街上看到一个留着长发的背影，大部分会猜测为一个女性，因为女性留长发的较多，当然也有可能是一些男性潮人，但在没有其他信息的情况下，我们会选择条件概率最大的类别，这就是朴素贝叶斯的思想基础：对于给出的待分类项，在此项出现在的条件下各个类别的出现概率，哪个最大，就认为此待分类项属于哪个类别。

从朴素贝叶斯分类的原理来看，对于一个未知类别的样本X,可以先分别计算出X属于每一个类别的概率，选择其中概率最大的类别作为其分类。还是上面的碗中球的例子，可能不是很恰当，但可以帮助理解。我们给每次拿球进行分类，碗A和碗B是两种分类，每次拿到球的颜色就是我们的特征，假如拿到了白色球，根据我们刚才的计算结果，来自碗A的概率是60%大于碗B是40%，那么如果我们对这次行为进行分类，这次拿球动作我们分类为碗A。这个不恰当的例子可以帮助我们理解朴素贝叶斯算法。

我们通过数学公式，说一下朴素贝叶斯分类算法：

假设X={A1,A2,A3,A4…Am}为一个待分类项，每个A为X的一个特性，C={Y1,Y2…Yn}为类别的集合。我们需要计算P(Y1|X), P(Y2|X)…(Yn|X)并取得中间最大的作为我们的分类结果。过程可以分为：

首先我们需要找一个已知分类的待分类项集合，作为训练集;统计得到在各个类别下各个特征属性的条件概率估计，即：

P(A1|Y1), P(A2|Y1)… P(Am|Y1), P(A1|Y2), P(A2|Y2)…P(Am|Yn)

朴素贝叶斯分类器是建立在一个条件独立性假设的基础之上，根据各个特征属性是条件独立的，则根据贝叶斯定理推导：

P(Yi|X)= P(X|Yi) P(Yi) / P(X)

其中分母P(X)表示X事件发生的概率，对于所有类别，都是同一个常数，所以，问题就转换成分子P(X|Yi)P(Yi)最大化即可，所以有：

P(X|Yi)P(Yi)= P(A1|Yi)P(A2|Yi)…P(Am|Yi) P(Yi)

最终，取得P(X|Yi)P(Yi)最大值，便得出分类结果。

总结下朴素贝叶斯分类的流程如下图：

总体来说完成朴素贝叶斯分类包含三个阶段：

第一阶段：准备工作。主要是根据具体情况确定特征属性，并对特征属性进行适当划分，形成训练样本集合。这一阶段输入的是所有待分类数据，输出是特征属性和训练样本。

第二阶段：分类器训练阶段。这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率即每个特征属性划分对每个类别的条件概率估计。输入是特征属性和训练样本，输出是分类器。

第三阶段：应用阶段。即使用分类器对待分类项进行分类，输入是分类器和待分类项，输出是待分类项和类别的映射关系。

3朴素贝叶斯分类优缺点及适用场景

优点：

1.朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。

2.对小规模的数据表现很好，能够处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。

3.对缺失数据不太敏感，算法也比较简单，常用于文本分类，欺诈检测。

缺点：

1.理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。

2.需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。

3.由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。

4.对输入数据的表达形式很敏感。

版权说明：感谢每一位作者的辛苦付出与创作，《数据私房菜》均在文章开头备注了原标题和来源。如转载涉及版权等问题，请发送消息至公号后台与我们联系，我们将在第一时间处理，非常感谢！