007：朴素贝叶斯

Posted 2021-04-25 奇异果说AI

朴素贝叶斯

贝叶斯学派的思想可以概括为：先验概率+数据=后验概率。也就是说我们在实际问题中需要得到的后验概率，可以通过先验概率和数据一起综合得到。先详细说下这个经历类似梵高的数学奇才——托马斯·贝叶斯。

好像能找到的只有这张素描

No1. 贝叶斯学派的由来

贝叶斯学派很古老，但是从诞生到一百年前一直不是主流。主流是频率学派。频率派的观点就是：人们对一件事情发生或不发生的概率，只有固定的0和1，即要么发生，要么不发生，从来不会去考虑某件事情发生的概率有多大，不发生的概率又是多大。而且概率虽然未知，但最起码是一个确定的值。比如如果问那时的人们一个问题：“有一个袋子，里面装着若干个白球和黑球，请问从袋子中取得白球的概率θ是多少？”他们会想都不用想，会立马告诉你，取出白球的概率就是1/2，要么取到白球，要么取不到白球，即θ只能有一个值，而且不论你取了多少次，取得白球的概率θ始终都是1/2，即不随观察结果的变化而变化。这种观点长期统治着人们的观念，直到后来一个名叫Thomas Bayes的出现。

托马斯·贝叶斯在世时，并不为当时的人们所熟知，很少发表论文或出版著作，与当时学术界的人沟通交流也很少，用现在的话来说，贝叶斯就是活生生一民间学术“屌丝”，可这个“屌丝”最终发表了一篇名为“An essay towards solving a problem in the doctrine of chances”，翻译过来则是：机会理论中一个问题的解。这篇论文的发表随机产生轰动效应，从而奠定贝叶斯在学术史上的地位。这篇论文可以用上面的例子来说明，“有一个袋子，里面装着若干个白球和黑球，请问从袋子中取得白球的概率θ是多少？”贝叶斯认为取得白球的概率是个不确定的值，因为其中含有机会的成分。比如，你的一个朋友要创业，你明明知道创业的结果就两种，即要么成功要么失败，但你依然会忍不住去估计他创业成功的几率有多大？以你对他的了解，他是一个有能力、有毅力、且能团结周围的人，你会不由自主的估计他创业成功的几率可能在80%以上。这种不同于最开始的“非黑即白、非0即1”的思考方式，便是贝叶斯的思考方式。

简单总结下频率派与贝叶斯派不同的思考方式：

• 频率派把需要推断的参数θ看做是固定的未知常数，即概率虽然是未知的，但最起码是确定的一个值，同时，样本 X 是随机的，所以频率派重点研究样本空间，大部分的概率计算都是针对样本 X 的分布。

• 而贝叶斯派的观点则截然相反，他们认为参数是随机变量，而样本 X 是固定的，由于样本是固定的，所以他们重点研究的是参数的分布。

贝叶斯派既然把参数或者特征看做是一个随机变量，所以要计算的分布，便得事先知道的无条件分布，即在有样本之前（或观察到X之前），有着怎样的分布呢？比如往台球桌上扔一个球，这个球会落在何处呢？如果是不偏不倚的把球抛出去，那么此球落在台球桌上的任一位置都有着相同的机会，即球落在台球桌上某一位置的概率服从均匀分布。这种在实验之前定下的属于基本前提性质的分布称为先验分布或者无条件分布。

其中，先验信息一般来源于以往经验跟资料。比如两位选手对决，解说一般会根据两位选手历次比赛的成绩对此次比赛的胜负做个大致的判断。再比如，某工厂每天都要对产品进行质检，以评估产品的不合格率θ，经过一段时间后便会积累大量的历史资料，这些历史资料便是先验知识，有了这些先验知识，便在决定对一个产品是否需要每天质检时便有了依据，如果以往的历史资料显示，某产品的不合格率只有0.01%，便可视为信得过产品或免检产品，只每月抽检一两次。而后验分布π（θ|X）一般也认为是在给定样本X的情况下的θ条件分布，而使π（θ|X）达到最大的值称为最大后验估计，类似于经典统计学中的极大似然估计。

综合起来看，则好比是人类刚开始时对大自然只有少得可怜的先验知识，但随着不断观察、实验获得更多的样本、结果，使得人们对自然界的规律摸得越来越透彻。所以，贝叶斯方法既符合人们日常生活的思考方式，也符合人们认识自然的规律，经过不断的发展，最终占据统计学领域的半壁江山，与经典统计学分庭抗礼。

No2. 贝叶斯定理

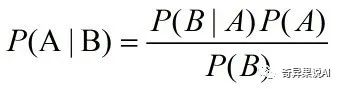
即：B条件下A成立的概率

这就将求后验概率 P(A|B) 的问题转变为求类先验概率 P(A) 和条件概率P(B|A)。先验概率 P(A) 表达了样本空间中各类样本所占的比例，根据大数定律，当训练集包含充足的独立同分布样本时，P(A) 可通过各类样本出现的频率来进行估计。因为对于类条件概率 P(B|A) 来说，由于它涉及关于 B 所有属性的联合概率，直接根据样本出现的频率来估计将会遇到严重的困难。假如样本的 D 个属性都是二值的，则样本空间将有 2 的 D 次方种可能取值，在现实中，这个种类数往往大于训练样本，也就是说，很多样本取值在训练集中根本没有出现，直接使用频率来估计 P(B|A) 显然不可行，因为“未被观测到”与“出现概率为零”通常是不同的。这可以通过极大似然估计来解决。

No3. 朴素贝叶斯

朴素贝叶斯只是贝叶斯定理的一个具体方法那朴素在哪里呢，它有两个前提条件：

• 一个特征出现的概率与其他特征（条件）独立。

• 每个特征同等重要。

举个例子来说明，假设有以下一组数据(程序员小王状态表)：

天气	打扮	女朋友是否在身边		状态
下雨	简约	在	-->	高兴
多云	精心打扮	没在	-->	兴奋
多云	邋遢	没在	-->	一般
... ...	... ...	... ...	... ...	... ...
下雨	精心打扮	没在	-->	郁闷
晴天	邋遢	在	-->	郁闷
晴天	简约	在	-->	？

根据贝叶斯定理预测：晴天打扮简约女朋友在身边的小王状态兴奋的概率？

P(晴天,简约,在,兴奋)=P(晴天|简约,在,兴奋)P(简约,在,兴奋)=P(晴天|简约,在,兴奋)P(简约|在,兴奋)P(在,兴奋)=P(晴天|简约,在,兴奋)P(简约|在,兴奋)P(在|兴奋)P(兴奋)# 朴素: 条件独立, 特征值之间没有任何关系=P(晴天|兴奋)P(简约|兴奋)P(在|兴奋)P(兴奋)

demo：‍

import numpy as npimport sklearn.naive_bayes as nbimport matplotlib.pyplot as mp
data = np.loadtxt('data.txt', unpack=False, delimiter=',')print(data.shape, data.dtype) # （400， 3）
x = np.array(data[:, :-1])y = np.array(data[:, -1])
mp.figure('Naive Bayes', facecolor='lightgray')mp.title('Naive Bayes', fontsize=16)mp.xlabel('X', fontsize=14)mp.ylabel('Y', fontsize=14)mp.tick_params(labelsize=10)# 通过样本数据,训练朴素贝叶斯分类模型model = nb.GaussianNB()model.fit(x, y)# 绘制分类边界线l, r = x[:, 0].min()-1, x[:, 0].max()+1b, t = x[:, 1].min()-1, x[:, 1].max()+1n = 500grid_x, grid_y = np.meshgrid( np.linspace(l, r, n), np.linspace(b, t, n))test_x = np.column_stack( (grid_x.ravel(), grid_y.ravel()))pred_test_y = model.predict(test_x)grid_z = pred_test_y.reshape(grid_x.shape)mp.pcolormesh(grid_x,grid_y,grid_z,cmap='gray')mp.scatter(x[:,0], x[:,1], s=60, c=y,  cmap='jet', label='Points')mp.legend()mp.show()

分类效果图

No4. 朴素贝叶斯算法的优缺点

优点：

• 算法逻辑简单,易于实现

• 分类过程中时空开销小（假设特征相互独立，只会涉及到二维存储）

缺点：

• 实际应用中属性个数比较多或者属性之间相关性较大时，分类效果不好。

最后，总结一下： 朴素贝叶斯分 类常用 于文本 分类， 尤其是对于 英文等语言来说，分类效果很好。 它常用于垃圾文本过滤、情感预测、推荐系统等。

“喜欢请关注”