基于贝叶斯定理的算法——朴素贝叶斯分类

Posted 2021-04-25 Stata and Python数据分析

文字编辑：孙晓玲

技术总编：张   邯

导读

通过前面的介绍我们知道， KNN 和决策树这两种算法虽然简单易懂，这两种算法在数据量较大时复杂度很高，一般只用在数据量较小的情况下，这样数据可以放入内存中运行。不过今天我们介绍的朴素贝叶斯分类器通过独立假设简化了概率的计算，节省了内存，可以很好地用于数据量大的情况。下面我们首先来了解这一算法的数理背景——贝叶斯定理。

算  法  原  理 

这一算法是由我们在概率论中学到的贝叶斯定理延伸出来的。我们知道贝叶斯公式为：

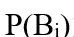其中， 为先验概率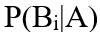， 为后验概率。而朴素贝叶斯就是要在先验概率的基础上将每个样本都归入后验概率最大的那一类中，由于P(A|B)难以从有限的训练样本中估计得到，因此采用了条件独立性假设——每个属性独立的对分类结果产生影响，这也是朴素贝叶斯中“朴素”二字的含义，它构成了这一分类的前提。

要使后验概率最大，由于属性和类别数都是不变的，因此只要使上式的分母最大，即：

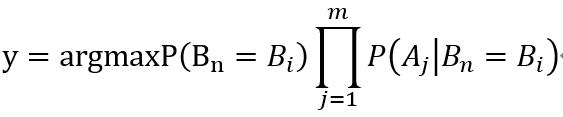
这就是朴素贝叶斯的推导式，对于不同的先验条件可以计算得到不同的模型，然后就可以利用得到的模型进行预测。

算  法  实  例 

我们对朴素贝叶斯的原理已经有了了解，下面我们使用sklearn库中的GaussianNB()来实现。这里我们使用的数据依然是自带的鸢尾花数据。程序如下：

from sklearn.datasets import load_irisfrom sklearn.model_selection import train_test_splitfrom sklearn.naive_bayes import GaussianNBfrom sklearn.metrics import accuracy_score #用来计算分类准确率
iris_sample = load_iris()x_train, x_test, y_train, y_test = train_test_split(iris_sample.data, iris_sample.target, test_size=0.25, random_state=123)nbclf = GaussianNB()nbclf.fit(x_train, y_train)y_test_pre = nbclf.predict(x_test)score = accuracy_score(y_test, y_test_pre) #accuracy_score(y_true, y_predict, normalize=True, sample_weight=None)，normalize为True时计算正确分类比例，否则计算的是样本数print('测试集预测结果为：', y_test_pre)print('测试集正确结果为：', y_test)print('测试集准确度为：', score)

分类结果及准确率如图：

可以看到分类的准确率达到94.74%。

在sklearn.naive中提供了三个分类器，分别为GaussianNB()、MultinomialNB()和ComplementNB()。我们来分别看看这三个类的参数。

（1）GaussianNB

GaussianNB假设特征的先验概率为正态分布，主要参数只有一个先验概率priors并默认不给出。该类有三种预测方法，最常用的predict方法直接给出测试集的预测类别，predict_proba给出测试集样本在各个类别上预测的概率，predict_log_proba则会给出predict_proba的一个对数转化。此外它还有一个partial_fit方法，如果训练集数据量非常大，不能一次全部载入内存，使用这个方法可以把训练集分成若干等分，重复调用partial_fit来一步步地学习训练集。但与前面的算法类不同，naive中的类都没有计算准确率的方法。

（2）MultinomialNB

MultinomialNB假设特征的先验概率为多项式分布，即：

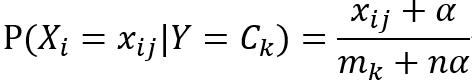
这个类中有三个参数，参数alpha即为上式中的α，默认取1，此时也称为拉普拉斯平滑；fit_prior表示是否要考虑先验概率，默认为True，当选择False时所有的样本类别输出都有相同的类别先验概率；class_prior用来输入先验概率，默认为None。该类所具有的预测方法与GaussianNB相同。

（3）BernoulliNB

BernoulliNB假设特征的先验概率为伯努利二项分布，它一共有4个参数，其中3个参数和MultinomialNB完全相同，剩下的那个参数binarize，当不传入取值时则将每个特征都看作二元，当传入数值时将小于binarize的归为一类，大于binarize归为另一类。此类的预测方法也与前两种一致。

如果样本特征大部分是连续值，一般会使用GaussianNB；如果样本特征大部分是多元离散值，则会使用MultinomialNB；而如果样本特征是二元离散值或者很稀疏的多元离散值，应该使用BernoulliNB。

以上就是我们对朴素贝叶斯分类器的介绍。

对我们的推文累计打赏超过1000元，我们即可给您开具发票，发票类别为“咨询费”。用心做事，不负您的支持！

往期推文推荐

关于我们

此外，欢迎大家踊跃投稿，介绍一些关于stata和python的数据处理和分析技巧。

投稿邮箱：[e-mail]

投稿要求：
1）必须原创，禁止抄袭；
2）必须准确，详细，有例子，有截图；
注意事项：
1）所有投稿都会经过本公众号运营团队成员的审核，审核通过才可录用，一经录用，会在该推文里为作者署名，并有赏金分成。
2）邮件请注明投稿，邮件名称为“投稿+推文名称”。
3）应广大读者要求，现开通有偿问答服务，如果大家遇到有关数据处理、分析等问题，可以在公众号中提出，只需支付少量赏金，我们会在后期的推文里给予解答。