朴素贝叶斯的引申

Posted 2021-04-25 阿华code

实际工程的小技巧

• log

• C = P(‘代开‘| L) * P(‘增值税‘| L) * P(‘发票‘| L) * P(‘确认‘| L) * P(‘后‘| L) * P(‘付款‘| L) * P(垃圾邮件)

• 可以看到上门的公司进行很多的乘法运算,计算的时间开销很大,对于篇幅很大的,比较耗时，把上面公式取log,实现加法，就快很多

• logC = logP(‘代开‘| L) + logP(‘增值税‘| L) + logP(‘发票‘| L) + logP(‘确认‘| L) + logP(‘后‘| L) + logP(‘付款‘| L) + logP(垃圾邮件)

• log计算不也是耗时吗？的确如此，但是可以在训练阶段直接计算log存在hash表里，在判断阶段直接取值相加即可。

• 转换权重

• 提高判断速度

• 
  

• 选取topk的关键词

• 通过分词选取k个关键词，将其权重相加，进行判断

• 分割文本

• 由于篇幅太长，关键词判断可能误判，所以对于长篇幅的分割文本，在取关键词取权重判断

• 位置权重

• 目前我们对语言的权重都没有考虑到邮件结构的因素。比如发票办理在标题中应该比在正文的权重影响更大。所以可以根据词语出现的位置，对其权重乘以放大系数，提高识别准确率

• 蜜罐

• 蜜罐是网络安全领域常用的手段，因其类似诱捕昆虫的罐子命名。其中的一种手段就是在各大论坛上公布自己注册的邮箱，收集垃圾邮寄...

贝叶斯方法的思维方式

• 讲了很多手段，都是建立在贝叶斯公式上的，所以下面看看贝叶斯方法的思维方式

  逆概问题

• 

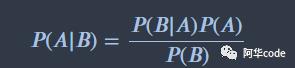
• 先不考虑P(X),P(Y),观察P(X|Y),P(Y|X)，可知贝叶斯揭示两个相反方向的条件概率之间的转换关系。其为了处理所谓的‘逆概’问题而诞生的。比如P(Y|X)不能通过直接观测来得到结果，而P(X|Y)却容易通过直接观测得到结果，就可以通过贝叶斯公式从间接观测对象去推断不可直接观测的对象情况

• 实例:基于邮件的文本内容判断其属于垃圾邮件的概率不好求(即不可直接观测、统计得到)，但是基于已经收集好的垃圾邮件样本，去统计(直接观测)其文本内部各个词语的概率就很方便

• 引申一步，基于文本特征去判断其所属标签不好求，但是基于已收集好的打上标签的样本（监督），却可以直接统计属于同一标签的样本内部各个特征的概率分布

  处理多分类问题

• 前面一直在说二分类，现在来看看多分类问题

• 还是用邮件分类问题，将邮件分为私人邮件、工作邮件、垃圾邮件。这里依次用1,Y2,Y3表示

• 

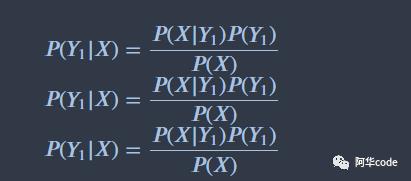
• 通过比较3个概率值的大小即可得到X所属的分类，由于分母一样，比较可以忽略

• 先验概率的问题

• 在垃圾邮件的例子中，先验概率都相等=1/3,所以上面公式可以改成 

• 这就是最大似然法，不考虑先验概率直接比较似然函数

下面介绍贝叶斯的实际工程的问题和代码实现文本分类。