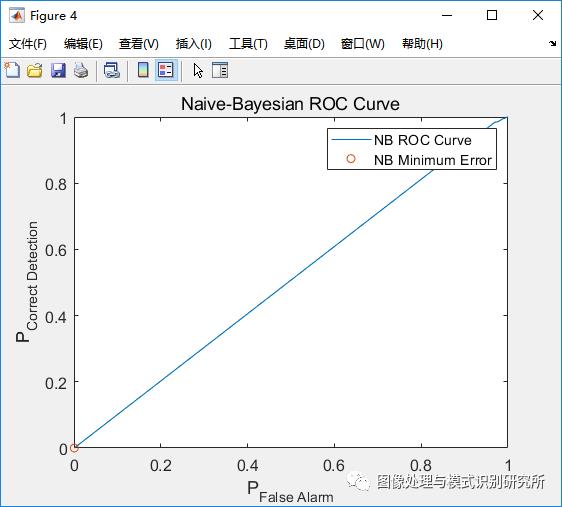
朴素贝叶斯和LDA分类规则产生显著较差的最小值。

Posted 2021-04-25 图像处理与模式识别研究所

♥

Q1.m

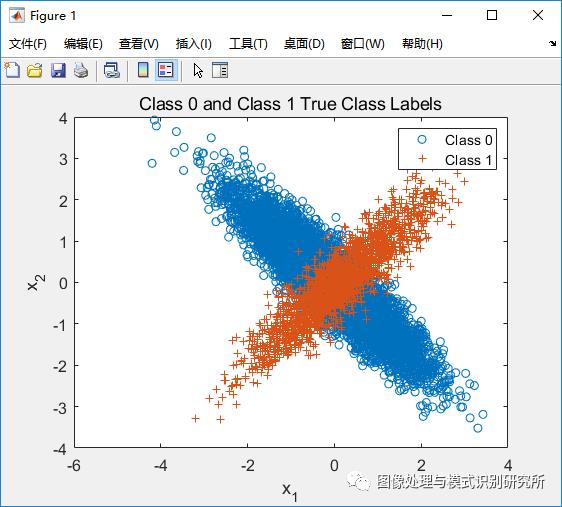
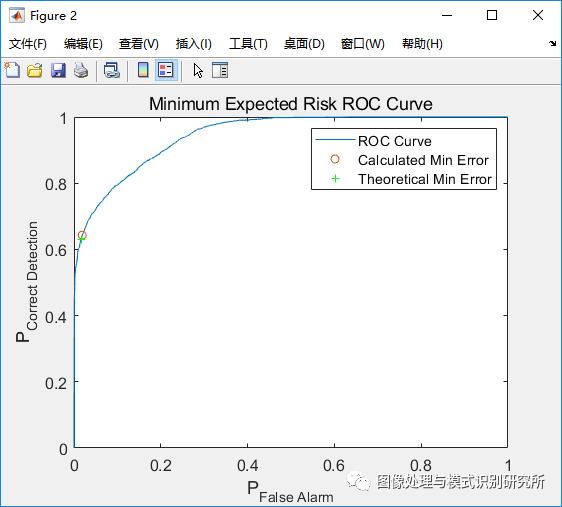
clear all; close all; clc;
n = 2; % # of dimensionsN = 10000; % # of samples
% Class mean and covariancemu(:,1) = [-0.1;0]; Sigma(:,:,1) = [1 -0.9;-0.9 1];mu(:,2) = [0.1;0]; Sigma(:,:,2) = [1 0.9; 0.9 1];
% Class priors and true labelsp = [0.8,0.2]; label = rand(1,N) >= p(1);Nc = [sum(label==0),sum(label==1)];
% Draw samples from each class pdfx = zeros(n,N);x(:,label==0) = mvnrnd(mu(:,1),Sigma(:,:,1),Nc(1))';x(:,label==1) = mvnrnd(mu(:,2),Sigma(:,:,2),Nc(2))';
% Plot true class labelsfigure(1);plot(x(1,label==0),x(2,label==0),'o',x(1,label==1),x(2,label==1),'+');title('Class 0 and Class 1 True Class Labels')xlabel('x_1'), ylabel('x_2')legend('Class 0','Class 1')
%% ======================== Question 1: Part 1 ======================== %%% Calculate discriminant scores and taudiscriminantScore = log(evalGaussian(x,mu(:,2),Sigma(:,:,2))./evalGaussian(x,mu(:,1),Sigma(:,:,1)));tau = log(sort(discriminantScore(discriminantScore >= 0)));
% Find midpoints of tau to use as threshold valuesmid_tau = [tau(1)-100 tau(1:end-1) + diff(tau)./2 tau(length(tau))+100];
% Make decision for every threshold and calculate error valuesfor i = 1:length(mid_tau) decision = (discriminantScore >= mid_tau(i)); pFA(i) = sum(decision==1 & label==0)/Nc(1); % False alarm prob. pCD(i) = sum(decision==1 & label==1)/Nc(2); % Correct detection prob. pE(i) = pFA(i)*p(1)+(1-pCD(i))*p(2); % Total error prob.end
% Find minimum error and corresponding threshold[min_error,min_index] = min(pE);min_decision = (discriminantScore >= mid_tau(min_index));min_FA = pFA(min_index); min_CD = pCD(min_index);
% Find theoretical minimum error(threshold calculated using class priors)ideal_decision = (discriminantScore >= log(p(1)/p(2)));ideal_pFA = sum(ideal_decision==1 & label==0)/Nc(1); % False alarmideal_pCD = sum(ideal_decision==1 & label==1)/Nc(2); % Correct detectionideal_error = ideal_pFA*p(1)+(1-ideal_pCD)*p(2);
% Plot ROC curve with minimum error point labeledfigure(2); plot(pFA,pCD,'-',min_FA,min_CD,'o',ideal_pFA,ideal_pCD,'g+');title('Minimum Expected Risk ROC Curve'); legend('ROC Curve', 'Calculated Min Error', 'Theoretical Min Error');xlabel('P_{False Alarm}'); ylabel('P_{Correct Detection}');
% Print all resultsfprintf('<strong>Theoretical Results</strong>\n');fprintf('Minimum probability of error: %.2f%%\nThreshold Value: %.2f\n',ideal_error*100,p(1)/p(2));
fprintf('\n<strong>Calculated Results</strong>\n');fprintf('Minimum probability of error: %.2f%%\nThreshold Value: %.2f\n\n',min_error*100,exp(mid_tau(min_index)));
%% ======================== Question 1: Part 2 ======================== %%Sigma_NB(:,:,1) = [1 0;0 1]; Sigma_NB(:,:,2) = [1 0;0 1];
% Calculate discriminant scores and taudiscriminantScore_NB = log(evalGaussian(x,mu(:,2),Sigma_NB(:,:,2))./evalGaussian(x,mu(:,1),Sigma_NB(:,:,1)));tau_NB = log(sort(discriminantScore_NB(discriminantScore_NB >= 0)));
% Find midpoints of tau to use as threshold valuesmid_tau_NB = [tau_NB(1)-1 tau_NB(1:end-1) + diff(tau_NB)./2 tau_NB(length(tau_NB))+1];
% Make decision for every threshold and calculate error valuesfor i = 1:length(mid_tau_NB) decision_NB = (discriminantScore_NB >= mid_tau_NB(i)); pFA_NB(i) = sum(decision_NB==1 & label==0)/Nc(1); % False alarm prob. pCD_NB(i) = sum(decision_NB==1 & label==1)/Nc(2); % Correct detection prob. pE_NB(i) = pFA_NB(i)*p(1)+(1-pCD_NB(i))*p(2); % Total error prob.end
% Find minimum error and corresponding threshold[min_error_NB,min_index_NB] = min(pE_NB);min_decision_NB = (discriminantScore >= mid_tau_NB(min_index_NB));min_FA_NB = pFA_NB(min_index_NB); min_CD_NB = pCD_NB(min_index_NB);
% Plot ROC curve with minimum error point labeledfigure(4); plot(pFA_NB,pCD_NB,'-',min_FA_NB,min_CD_NB,'o');title('Naive-Bayesian ROC Curve'); legend('NB ROC Curve', 'NB Minimum Error');xlabel('P_{False Alarm}'); ylabel('P_{Correct Detection}');
fprintf('\n<strong>Calculated Results, Naive-Bayesian</strong>\n');fprintf('Minimum probability of error: %.2f%%\nThreshold Value: %.2f\n\n',min_error_NB*100,exp(mid_tau_NB(min_index_NB)));
%% ======================== Question 1: Part 3 ======================== %%% Code help and example from Prof. Deniz% LDA setupSb = (mu(:,1)-mu(:,2))*(mu(:,1)-mu(:,2))';Sw = Sigma(:,:,1) + Sigma(:,:,2);
% Calculating Fisher LDA projection vector[V,D] = eig(inv(Sw)*Sb); % alpha w = inv(Sw) Sb w[~,ind] = sort(diag(D),'descend');wLDA = V(:,ind(1)); % Fisher LDA projection vectoryLDA = wLDA'*x; % All data projected on to the line spanned by wLDAwLDA = sign(mean(yLDA(find(label==1)))-mean(yLDA(find(label==0))))*wLDA; % ensures class 1 falls on the + side of the axisyLDA = sign(mean(yLDA(find(label==1)))-mean(yLDA(find(label==0))))*yLDA; % flip yLDA accordingly
% Plot LDA projectionfigure(5);plot(yLDA(find(label==0)),zeros(1,Nc(1)),'o',yLDA(find(label==1)),zeros(1,Nc(2)),'+');title('LDA projection of data points and their true labels');xlabel('x_1'); ylabel('x_2'); legend('Class 0','Class 1');
% Sort LDA projection vector and find midpointssorted_yLDA = sort(yLDA);mid_tau_LDA = [sorted_yLDA(1)-1 sorted_yLDA(1:end-1)+diff(sorted_yLDA)./2 sorted_yLDA(length(sorted_yLDA))+1];
% Make decision for every threshold value and find error probabilitiesfor i = 1:length(mid_tau_LDA)-1 decisionLDA = (yLDA >= mid_tau_LDA(i)); pFA_LDA(i) = sum(decisionLDA==1 & label==0)/Nc(1); % False alarm pCD_LDA(i) = sum(decisionLDA==1 & label==1)/Nc(2); % Correct detection pE_LDA(i) = pFA_LDA(i)*p(1)+(1-pCD_LDA(i))*p(2);end
% Find minimum error and corresponding threshold[min_error_LDA,min_index_LDA] = min(pE_LDA);min_decision_LDA = (yLDA >= mid_tau_LDA(min_index_LDA));min_FA_LDA = pFA_LDA(min_index_LDA); min_CD_LDA = pCD_LDA(min_index_LDA);
% Plot LDA ROC Curvefigure(6); plot(pFA_LDA,pCD_LDA,'-',min_FA_LDA,min_CD_LDA,'o');title('Fisher LDA ROC Curve'); legend('LDA ROC Curve', 'LDA Minimum Error');xlabel('P(False Alarm)'); ylabel('P(Correct Detection)');
%Print Resultsfprintf('\n<strong>Calculated Results, LDA</strong>\n');fprintf('Minimum probability of error: %.2f%%\nThreshold Value (tau): %.2f\n\n',min_error_LDA*100,mid_tau_LDA(min_index_LDA));
%% ======================= Question 1: Functions ====================== %%% Function credit: Prof. Denizfunction g = evalGaussian(x,mu,Sigma)% Evaluates the Gaussian pdf N(mu,Sigma) at each coumn of X[n,N] = size(x);
C = ((2*pi)^n * det(Sigma))^(-1/2); % coefficientE = -0.5*sum((x-repmat(mu,1,N)).*(inv(Sigma)*(x-repmat(mu,1,N))),1); % exponentg = C*exp(E); % final gaussian evaluation
end