机器学习(算法篇)-朴素贝叶斯分类
Posted 仓储进化
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了机器学习(算法篇)-朴素贝叶斯分类相关的知识,希望对你有一定的参考价值。
月饼
快中秋了,小朋友第一次见月饼:
“ 这是什么,我没见过 ”
“ 这是面包吗 ?”
“ 这是馒头吗 ?”
“ 这是包子吗 ?”
“ 我不知道这是什么,但我知道能吃 ”
那你尝一尝看 ?
" 像面包 "
朴素贝叶斯原理
贝叶斯原理是英国数学家托马斯·贝叶斯提出的。一个很神奇的人,他的经历类似梵高。生前没有得到重视,死后,他写的一篇关于归纳推理的论文被朋友翻了出来,并发表了。这一发表不要紧,结果这篇论文的思想直接影响了接下来两个多世纪的统计学
贝叶斯为了解决一个叫“逆向概率”的问题,尝试解答在没有太多可靠证据的情况下,怎样做出更符合数学逻辑的推测。
什么是“逆向概率”呢?
所谓“逆向概率”是相对“正向概率”而言。
正向概率的问题很容易理解,比如我们已经知道袋子里面有 N 个球,不是黑球就是白球,其中 M 个是黑球,那么把手伸进去摸一个球,就能知道摸出黑球的概率是多少。
但这种情况往往是上帝视角,即了解事情的全貌再做判断。
如上图:已知10个球,4个白色,6个黑色的,
随机摸一个球,是黑色的概率是多少?
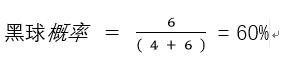
但是,在现实生活中,而一个自然而然的问题是反过来, 我们很难知道事情的全貌。
贝叶斯则从实际场景出发,提了一个问题:如果我们事先不知道袋子里面黑球和白球的比例,而是通过我们摸出来的球的颜色,能判断出袋子里面黑白球的比例么?
这个问题,就是所谓的逆向概率问题
正是这样的一个问题,影响了接下来近 200 年的统计学理论。
这是因为,贝叶斯原理与其他统计学推断方法截然不同,它是建立在主观判断的基础上:在我们不了解所有客观事实的情况下,同样可以先估计一个值,然后根据实际结果不断进行修正。
特别地,贝叶斯是机器学习的核心方法之一。
这背后的深刻原因在于:
现实世界本身就是不确定的,人类的观察能力是有局限性的 。
实际上,贝叶斯当时的论文只是对这个问题的一个直接的求解尝试,并不清楚 是不是已经意识到这里面包含着的深刻的思想。然而后来,贝叶斯方法席卷了概率论,并将应用延伸到各个问题领域,所有需要作出概率预测的地方都可以见到贝叶斯方法的影子
先验概率 后验概率
百科:
先验概率是指根据以往经验和分析得到的概率,如全概率公式,它往往作为"由因求果"问题中的"因"出现.
后验概率是指依据得到"结果"信息所计算出的最有可能是那种事件发生,如贝叶斯公式中的,是"执果寻因"问题中的"因"
我的理解:
先验: 由原因可直接推测出结果:
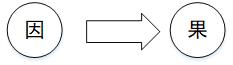
后验:结果已经产生,推测哪些原因引起的
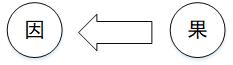
从原因到结果的论证称为“先验的”,
而从结果到原因的论证称为“后验的”。
先验概率和后验概率的区别:
先验概率基于已有知识对随机事件进行概率预估,但不考虑任何相关因素。
后验概率基于已有知识对随机事件进行概率预估,并考虑相关因素,可不断修正。
贝叶斯公式

其中:
P(A|B)表示后验概率,是在 B 发生的情况下 A 发生的可能性 (后验概率)
P(B|A) 表示先验概率
记住这个就可以了:
后验概率 = 先验概率 x 调整因子
我们用小朋友吃月饼的过程,模拟下:
1、 先验概率:
没见过月饼,根据以往的经验(特征值) 判断
比如根据颜色:都是淡黄色的, 判断可能是面包,
比如圆圆形状又有馅,猜测可能是包子
2、调整因子
根据获取的部分特征 来修正,
小朋友尝了一口,根据味道判断 像面包 而不是包子
3、 后验判断
通过调整因子修正后,得出结论是 面包
( 月饼一个传统美食,现在做的越来越像西餐的糕点 )
贝叶斯推断的含义:
我们先预估一个"先验概率"
然后加入实验结果,看这个实验到底是增强还是削弱了"先验概率"
由此得到更接近事实的"后验概率"
后验概率 = 先验概率 x 调整因子
如果"调整因子 ">1
意味着"先验概率"被增强,事件A的发生的可能性变大;
如果"调整因子"=1,
意味着B事件无助于判断事件A的可能性;
如果"调整因子"<1,
意味着"先验概率"被削弱,事件A的可能性变小。
通常,事件 A 在事件 B 发生的条件下的概率,与事件 B 在事件 A 发生的条件下的概率是不一样的;然而,这两者是有确定关系的,贝叶斯定理就是这种关系的陈述。
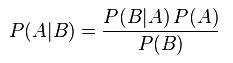
贝叶斯公式的用途在于通过己知三个概率来推测第四个概率。它的内容是:在 B 出现的前提下,A 出现的概率等于 A 出现的前提下 B 出现的概率乘以 A 出现的概率再除以 B 出现的概率。通过联系 A 与 B,计算从一个事件发生的情况下另一事件发生的概率,即从结果上溯到源头(也即逆向概率)。
通俗地讲就是当你不能确定某一个事件发生的概率时,你可以依靠与该事件本质属性相关的事件发生的概率去推测该事件发生的概率。用数学语言表达就是:支持某项属性的事件发生得愈多,则该事件发生的的可能性就愈大。这个推理过程有时候也叫贝叶斯推理。
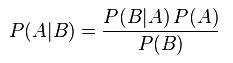
在贝叶斯定理中,每个名词都有约定俗成的名称
P(A)是 A 的先验概率,之所以称为“先验”是因为它不考虑任何 B 方面的因素。
P(A|B)是已知 B 发生后 A 的条件概率,也由于得自 B 的取值而被称作 A 的后验概率。
P(B|A)是已知 A 发生后 B 的条件概率,也由于得自 A 的取值而被称作 B 的后验概率。
P(B)是 B 的先验概率,也作标准化常量
举个例子
《决策与判断》
第十二章中讲到人们都有保守主义情结,即使出现了新信息,也不愿意根据新信息来更新先验概率。
用前面解释里面的话说就是:新信息是 B 事件不断发生,人们本应该根据这个信息去更新 A 事件发生的概率,但人们却更愿意固守之前估计的 A 事件发生的概率
书中举了这样一个调查案例:
假设有两个各装了100个球的箱子,甲箱子中有70个红球,30个绿球,乙箱子中有30个红球,70个绿球。假设随机选择其中一个箱子,从中拿出一个球记下球色再放回原箱子,如此重复12次,记录得到8次红球,4次绿球。问题来了,你认为被选择的箱子是甲箱子的概率有多大?


即 根据获取红球的概率 猜测是甲箱概率
贝叶斯公式: P(甲箱|红球)

P(红球|甲箱) = 在甲箱获取红球的概率 = 70% = 0.7
p(甲箱)= 拿红球是甲箱的概率(第一次50%,不是甲箱就是乙箱)
= 0.5
P(红球)= 红球全概率
= 甲箱的红球概率 * 是甲箱的概率 + 乙箱的红球概率*是乙箱的概率
= 0.7 * 0.5 + 0.3 *0.5

如果第一次拿的是红球,刚开始选择是甲箱或者乙箱子的先验概率都是50%
即在出现一个红球之后,甲乙箱子被选中的先验概率就被修正为:
P(甲) = 0.7, P(乙) = 1 - P(甲) = 0.3;
第二次还是红球,判断是甲箱的概率:修正因子变了

为了好理解,第三个还是红球,是甲箱子先验的概率修正为:
P(甲) = 0.8448, P(乙) = 1 - P(甲) = 0.1552 ;

如此重复,直到经历8次红球修正(概率增加),
4次绿球修正(概率减少),调整因子小于1,
之后,选择的是甲箱子的概率为:96.7%。
调查结果显示,大部分人都低估了选择的是甲箱子的概率 。
用一段 Python 代码来解这个问题:
计算选择的是甲箱子的概率
这些例子来至 CSDN:
#贝叶斯公式# 参数: 先验概率,甲箱的概率,乙箱的概率def bayesFunc(pIsBox1, pBox1, pBox2):return (pIsBox1 * pBox1)/((pIsBox1 * pBox1) + (1 - pIsBox1) * pBox2)# 先验概率,默认值0.5,# 第一次拿的是红球,甲箱和乙箱的概率相同def redGreenBallProblem():pIsBox1 = 0.5# 8次拿红球的 后验概率for i in range(1, 9):pIsBox1 = bayesFunc(pIsBox1, 0.7, 0.3)print " After red %d > in 甲 box: %f" % (i, pIsBox1)# 四次拿绿球的后验概率for i in range(1, 5):pIsBox1 = bayesFunc(pIsBox1, 0.3, 0.7)print " After green %d > in 甲 box: %f" % (i, pIsBox1)redGreenBallProblem()
程序运行结果如下:在这个调查问题里面,8次红球与4次绿球出现的顺序并不重要,因为红球的出现总是使选择的是甲箱子的概率增加,而绿球的出现总是减少。因此,为了简化编程,我将红球出现的情况以及绿球出现的情况摆在一起了。
不断修正的选择的是甲箱子的先验概率
# 全是红球的时候,概率逐步增高After red 1 > in 甲 box: 0.700000After red 2 > in 甲 box: 0.844828After red 3 > in 甲 box: 0.927027After red 4 > in 甲 box: 0.967365After red 5 > in 甲 box: 0.985748After red 6 > in 甲 box: 0.993842After red 7 > in 甲 box: 0.997351# 8个全是红球时,甲箱子的最高概率After red 8 > in 甲 box: 0.998863# 获取绿球开始,判断是甲箱的概率逐步降低# 也符合预期,After green 1 > in 甲 box: 0.997351After green 2 > in 甲 box: 0.993842After green 3 > in 甲 box: 0.985748After green 4 > in 甲 box: 0.967365
总结
朴素贝叶斯,通过局部猜测全局,以小见大 。
古人的智慧:一叶落知天下秋
2020-09-07 深圳 多云
看往期:
大数据
以上是关于机器学习(算法篇)-朴素贝叶斯分类的主要内容,如果未能解决你的问题,请参考以下文章