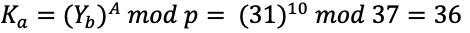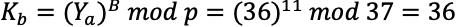探秘密码学：深入了解对称加密与密钥协商技术

Posted 2021-04-25 京东智联云开发者

作者丨京东智联云-平台安全组 张惊申

密码，已经成为当代互联网人每天使用频率最高的东西，它在默默地守护着我们的信息安全。而人们对密码却始终未给予足够重视，以至于经常会出现“123456”这种弱密码。你可能会觉得好笑，但这个密码常年稳居最常见的密码排行榜榜首，有250万人在使用，在数据泄露方面的暴露次数超过2300万次，黑客只需不到一秒钟就可以成功破解。

 

好在我们的社会中，总有那么一群人在不断研究着密码学，保护着我们的信息安全、系统安全。密码学历史悠久，其首要目的是隐藏信息的涵义，并不是隐藏信息的存在。密码学也促进了计算机科学，特别是在于电脑与网络安全所使用的技术，如访问控制与信息的机密性。密码学已被应用在日常生活：包括自动柜员机的芯片卡、电脑使用者存取密码、电子商务等等。

 

密码学是一门浩瀚的学科，无数的学者和研究人员数十年钻研往往也仅能取得非常微小的成绩。下图为笔者对密码学框架的部分理解，足以见得密码这门学科的博大精深。本文选取密码学学科中的一小部分内容进行介绍和演示。

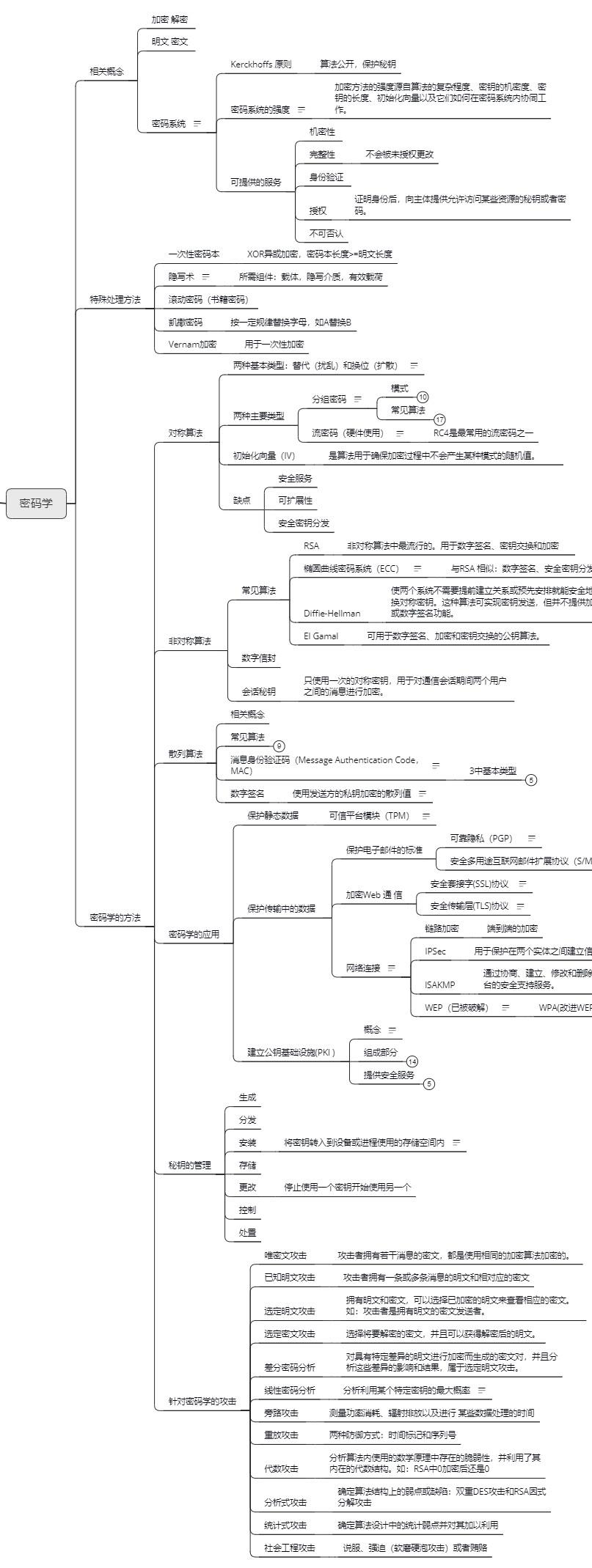
▲图1 对密码学学科框架的部分理解▲

加密的理论基础是替代和换位。替代主要用于扰乱，使用不同的位、字符或字符分组来替换原来的位、字符或字符分组。换位主要用于扩散，并不使用不同的文本来替换原来的文本，而是对原有的值进行置换，即重新排列原来的位、字符或字符分组以隐藏其原有意义。

 

对称加密是一种加密与解密采用相同密钥的加密算法。其特点是速度快，效率高，所以被广泛使用在很多加密协议的核心当中，也是我们平时接触得比较多的一种加密方式。

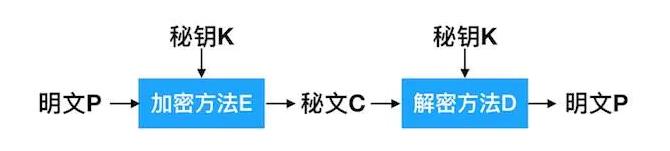
▲图2 对称加密算法加密解密过程▲

 

常见的对称加密算法主要有以下几种：

1. 数据加密标准（DES，Data Encryption Standard），使用64位密钥，其中56位用于加密，8位用于奇偶校验。由于加密强度较弱，已不推荐使用；

2. 三重DES，是DES的升级版。3DES并没有直接使用“加密->加密->加密” 的方式，而是采用了“加密->解密->加密”的方式。这样实现的好处主要是，当三个密钥均相同时，前两步加密解密结果相互抵消，整体结果相当于仅实现了一次加密，因此可实现对普通DES加密算法的兼容。这也是为什么三重DES可以流行，而二重DES或者四重DES则消失了；

3. 高级加密标准（AES，Advanced Encryption Standard），AES支持128、192和256位的密钥，较于3DES速度更快、安全性更高；

4. 国际数据加密算法（IDEA，International Data Encryption Algorithm），使用的密钥长度为128位；

5. Blowfish算法，密钥长度为32-448位。

对称加密需要双方进行加密通信前先协商分配好密钥，一般来说密钥分发可以是以下几种方式：

1. Alice选择一个密钥后以物理的方式传递给Bob；

2. 第三方Cindy选择密钥后物理地传递给Alice和Bob；

   
   

3. 如果Alice和Bob之前已经使用过一个密钥，则一方可以将新密钥用旧密钥加密后发送给另一方；

4. 如果Alice和Bob与第三方Cindy之间已有加密连接，则Cindy可以在加密连接上将密钥发送给Alice和Bob。

 

受对称加密算法自身的特点影响，当多用户之间使用对称加密算法进行通信时，密钥数量成指数增长，对密钥的分发和管理带来巨大的挑战。当用户数量为n，密钥数量最多为n*(n-1)/2。比如有100个用户，则最多需要4950个密钥。

随着技术的发展，对称加密的密钥分发也出现了一些新的解决方法，如非对称加密算法，Diffie–Hellman算法等。采用这类算法使得对称加密密钥的协商与管理变得更简单和可靠。采用非对称加密时n个用户只需维护n个密钥对，大大减小了密钥规模。

Diffie-Hellman算法（简称DH算法）是Whitefield Diffie和Martin Hellman在1976年公布的一种秘钥交换算法。它是一种建立秘钥的方法，而不是加密方法。基于这种秘钥交换技术：通信双方在完全没有对方任何预先信息的条件下，可以通过不安全信道协商一个密钥。这个密钥一般作为对称加密的密钥应用在双方后续数据传输的加密上。

 

和非对称加密算法的理论基础一样，DH算法也是基于一个数学难题，即计算离散对数的难度。具体来说，假设Alice需要与Bob需要协商一个秘钥，是这样一个过程：

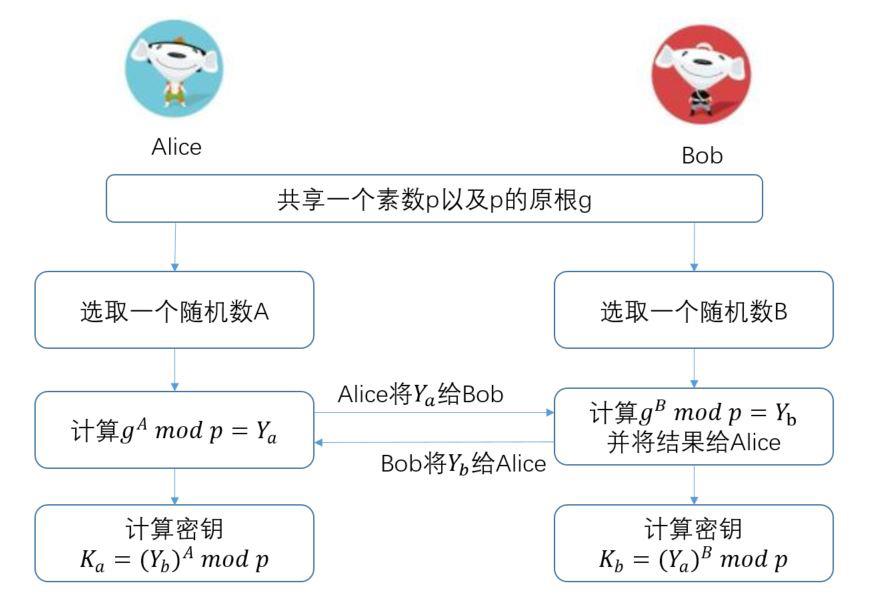
▲图3 DH算法密钥协商过程▲

1. 首先Alice与Bob共享一个素数p以及p的原根g，当然这里有2≤g≤p-12≤g≤p-1。这两个数是可以不经过加密地由一方发送到另一方，至于谁发送给并不重要，其结果只要保证双方都得知p和g即可。

2. 然后Alice产生一个私有的随机数A，满足1≤A≤p-1，然后计算，将结果 通过公网发送给Bob。

3. Bob也产生一个私有的随机数B，满足1≤B≤p-1，计算 ，将结果 通过公网发送给Alice。

4. 双方计算密钥。

 

Alice知道的信息有p，g，A，，，其中数字A是Alice私有的，只有她自己知道，别人不可能知道。p，g，A都是别人有可能知道的，是Bob发送给Alice的；

Bob知道的信息有p，g，B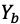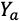，，，其中数字B是Bob私有的，只有他自己知道，别人不可能知道。p，g，B是别人有可能知道的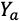，是Alice发送给Bob的。

上面的过程中，Alice和Bob之间的秘钥协商完成，密钥具体计算方法如下：

Alice通过计算 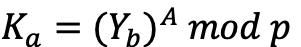得到秘钥；

Bob通过计算 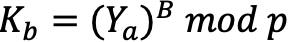得到秘钥。

通过计算可以得到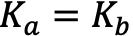，，即双方协商结算出的密钥相同，可以将该密钥作为对称加密密钥使用：

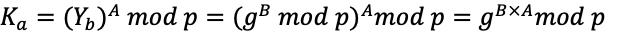
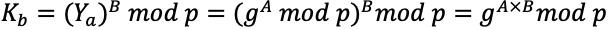
由上证明过程可见，Alice和Bob生成秘钥时，其实是进行了相同的运算过程，因此必然有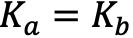。这也是双方能够进行秘钥协商的根本原因。

1. 首先Alice与Bob共享一个素数37以及原根6（37的原根：3，6，11，12，13，15，17，21，22，23，24，26，27，29，可采用图4的方法生成）。

2. 然后Alice产生一个私有的随机数10，然后计算 ，将36发送给Bob；

   
   

3. Bob也产生一个私有的随机数11，计算 ，将结果31发送给Alice。

4. 双方计算密钥：

经计算，Alice与Bob本次协商的密钥为36。

原根计算方法python实现如下图所示：

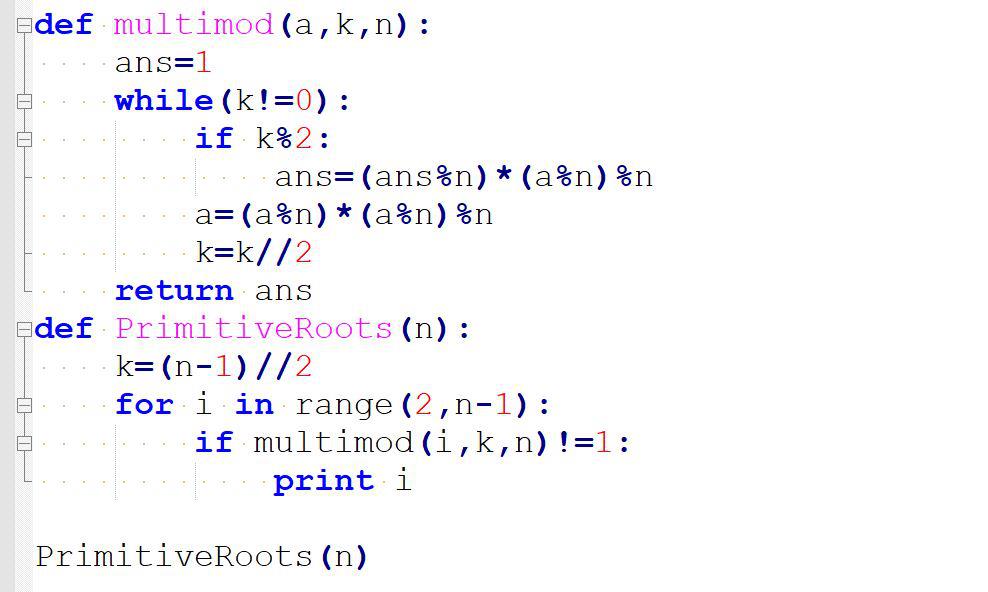
▲图4 原根计算方法python实现▲

对于DH算法来说，虽然双方在没有任何预先信息的条件下，可以完成密钥协商，但密钥协商过程也存在中间人攻击的风险。

 

现代密码学中的安全是基于密钥的保密性的，而不是古典密码学的算法的保密性。对于绝大部分普通用户或者组织，相对于去尝试自己开发一个加密算法，直接采用成熟的算法，把精力放在密钥保管上更为合理。