写给开发人员的实用密码学 - 对称加密算法

Posted 2021-04-25 云水木石

所谓数据加密，就是将一段数据处理成无规则的数据，除非有关键的密钥，否则谁也无法得知无规则数据的真实含义。

在密码学中，用于数据加密的算法主要有两种，分别是对称加密算法（Symmetric-key Algorithms）和非对称加密算法（Asymmetrical Cryptography）。

这篇文章先介绍比较容易理解的对称加密算法。

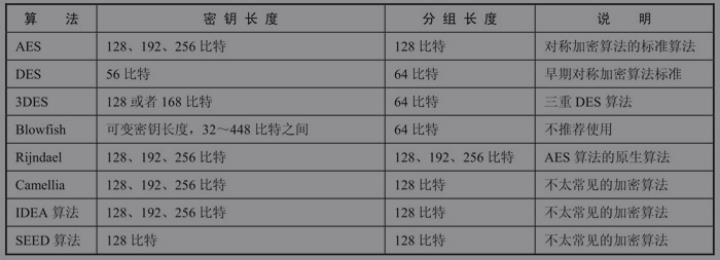
无论什么加密算法，密钥是非常重要的一环，加密和解密都需要用到，如果加密和解密的密钥相同，这种加密算法就属于对称加密算法。下图描述了对称加密算法的操作：

对称加密算法

加密和解密操作是一个互逆过程，算法涉及到复杂的数学知识，一般而言开发人员并不需要理解其细节。但即使是使用加密算法，我们也需要了解密钥长度、分组长度、填充模式等等知识，只有这样才能选择安全的加密算法。

首先，密钥长度是对称加密算法中非常关键的一个概念，密钥长度决定了算法的安全性。通常，加密算法都有好几种密钥长度的实现，比如 AES 128、AES 192、AES 256分别对应128 bit、192 bit和256 bit的密钥长度。同一种加密算法，密钥长度越长，算法越安全。

其次，对称加密算法有两种类型：块密码算法（block ciphers）和流密码算法（stream ciphers）。表 1 和表 2 列举了常用的块密码算法和流密码算法：

表1：块密码算法

表2：流密码算法

流密码算法使用的较少，在实际开发中，基本上采用块密码算法，所以这里只探讨块密码算法。

块密码算法

所谓块密码算法，就是在加密或这解密数据时，将数据分成固定长度的数据块（block），每次只处理一个数据块，依次对一个个的数据块加密或解密，最后完成对整个数据的加解密。

数据块的长度就称为分组长度（block size），由于大部分明文的长度远远大于分组长度，所有要经过多次迭代运算才能得到最终的密文或明文。最简单的方法是对数据块分别加密，然后合成一块数据，但这种方式并不安全，所以，人们为块密码算法设计了多种迭代模式（Block cipher modes of operation），迭代模式也可以称为分组模式。

此外，明文的长度通常不是分组长度的整数倍，而某些块加密算法只能处理固定长度的数据，所以对最后不足分组长度的数据，需要进行填充，这就是块密码算法中的填充机制，有对应的填充标准。

分组模式

刚开始接触对称加密算法时，对代码中的 ECB、CBC、CFB、OFB, CTR 和 GCM 等概念也是云里雾里，后来才知道，其实它们就是分组模式。

基本上，对一大块输入数据进行加密，过程是这样的：初始化加密算法状态（使用加密密钥+随机盐），对数据的第一部分进行加密，然后加密状态转换（使用加密密钥和其他参数），对下一部分进行加密，然后再次转换加密状态，对下一部分进行加密，依此类推，直到处理完所有输入数据为止。解密的工作方式非常相似。

• EBC 模式

ECB模式（Electronic Codebook）是最简单的一种迭代模式，这种迭代模式是存在安全问题的，一般不建议使用。为什么不安全呢，我们看看其加密过程，如下图所示：

ECB模式加密

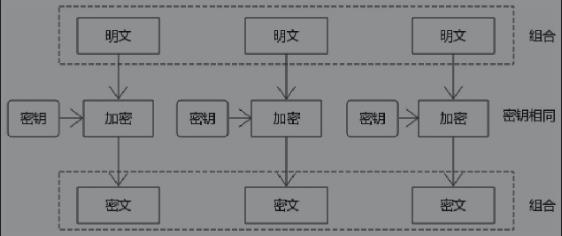
这个过程很容易理解：

1. 将明文拆分成多个数据块，每个数据块的长度等于分组长度，如果最后一个数据块长度小于分组长度，需要进行填充保证最后一个数据块长度等于分组长度。
2. 依次对每个数据块进行迭代得到每个数据块的密文分组，将所有密文分组组合在一起就得到最终的密文，密文长度等同于明文长度。

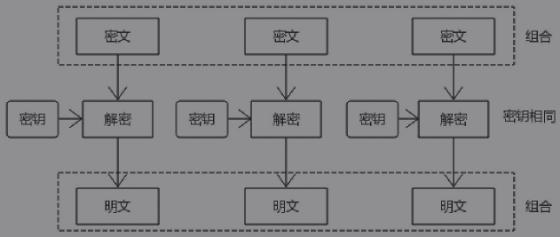
解密过程类似：

ECB模式解密

为什么这种分组模式存在安全问题呢？这是由于固定的明文和密钥每次运算的结果都是相同的，很容易被人找出规律。举个例子：

ECB模式解密

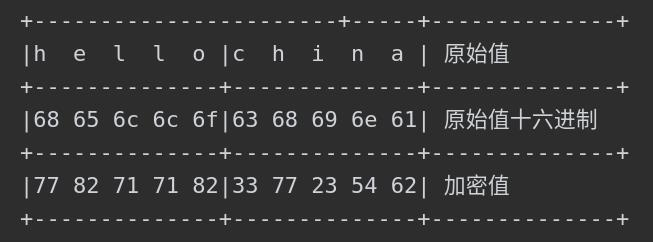
“hellochaia”这个字符串对于同一个密钥来说，经过两次迭代运算得到的密文值永远是不变的，攻击者截取到密文很容易发现加密采用的是ECB模式，从而可以观察到很多规律，比如密文中多次出现71，最终可能能成功破解出明文。

即使攻击者不能破解，也可以篡改密文，比如将所有的71替换为77，然后再将篡改的数据发送给接收者，接收者最终根据密钥反解得到字符串“hehhochina”，可这个字符串并不是原始明文，虽然能够正确解密但是明文已经被篡改了。

• CBC 模式

CBC 模式解决 ECB 模式的安全问题，为什么这么说呢？先看看其加密过程：

CBC模式加密

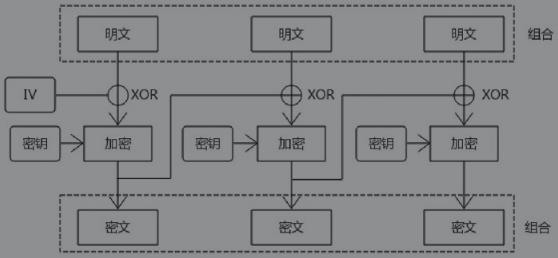
1. 将密文拆分成多个数据块，每个数据块的长度等于分组长度，如果最后一个数据块长度小于分组长度，需要进行填充保证最后一个数据块长度等于分组长度。
2. 首先处理第一个数据块，生成一个随机的初始化向量IV（InitializationVector），初始化向量和第一个数据块进行XOR运算，运算的结果经过加密得到第一个密文分组。
3. 接着处理后续的数据块，第n个数据块会和前n-1密文分组进行XOR运算，运算的结果再进行加密得到第n个密文分组。
4. 将各个密文分组组合在一起就是完整的密文。

从加密过程可以看到：

1. 初始化向量是随机的（必须每次都不一样），所以同样的明文和密钥最终得到的密文是不一样的。
2. 每个数据块（明文或者密文）和上一个数据块之间都是有关联的，上一个数据块稍有变化，最终得到的结果完全不一样。

这样就很好解决了 ECB 模式存在的安全问题。

解密过程如下图所示：

CBC模式解密

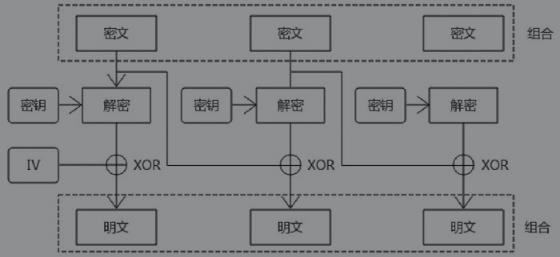
CBC加密模式非常常见，但是使用起来很烦琐，如果应用不当，很容易出现问题，需要注意以下几点：

1. 初始化向量必须每次都不一样。
2. 一般情况下初始化向量和密文是同时传输给解密者的，而且初始化向量是不加密的。
3. 迭代运算数据块不能并行处理，只有处理完第n个数据块，才能继续处理第n+1个数据块。

• CTR 模式

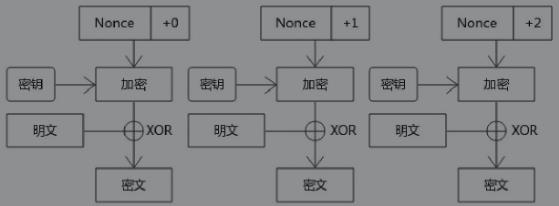
下图说明了如何在 CTR 块操作模式下使用块密码对明文的块进行逐个加密：

CTR模式加密

1. 将密文拆分成多个数据块，和CBC迭代不一样的是不需要进行填充处理。
2. 在处理迭代之前，先生成每个密钥流，有n个数据块，就有n个密钥流。根据第n个密钥流可以得到第n+1个密钥流，最简单的方式就是密钥流每次递增加一。
3. 第一个密钥流的获取方式也很简单，就是生成一个随机值（Nonce），Nonce和IV可以等同理解，一个不容易推导出来的随机值。
4. 接下来进行迭代加密处理，密钥流和密钥进行处理，得到的值再和数据块进行XOR运算（每次迭代相当于流密码运行模式）得到密文分组。
5. 迭代运行每个数据块，最终得到密文。

解密过程如下图所示：

CTR模式解密

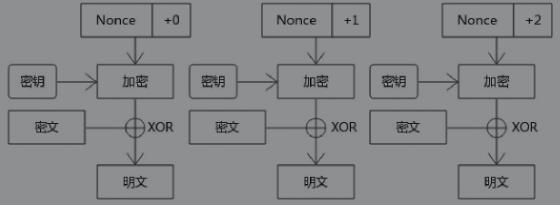
和 CBC 模式不同之处在于数据块无需填充。

• GCM (Galois/Counter) 模式

下图直观地说明了GCM块模式的工作方式：

GCM模式加密

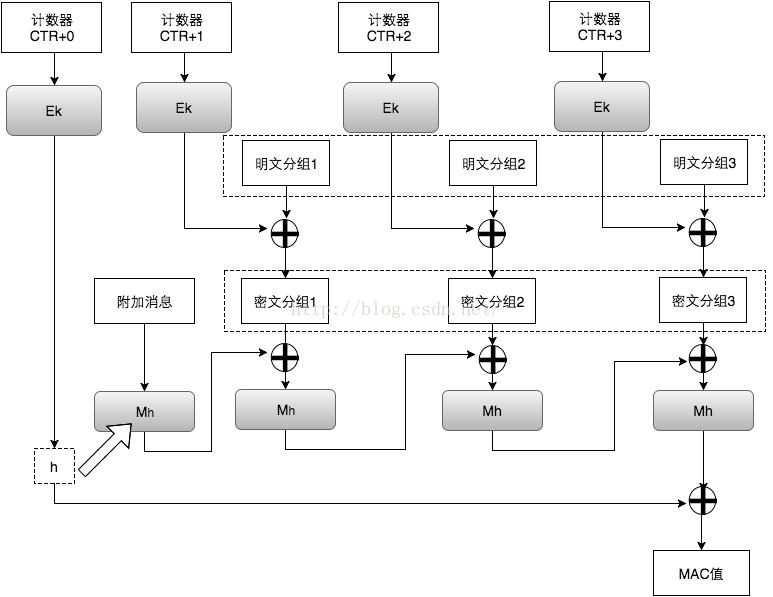
GCM 模式使用一个计数器，该计数器针对每个块增加，并在每个已处理的块之后计算消息身份验证标签（MAC代码）。最终的 MAC 值是从最后一个块计算得出的。

GCM 可以提供对消息的加密和完整性校验，另外，它还可以提供附加消息的完整性校验。在实际应用场景中，有些信息是我们不需要保密，但信息的接收者需要确认它的真实性的，例如源IP、源端口、目的IP、IV，等等。因此，我们可以将这一部分作为附加消息加入到 MAC 值的计算当中。最后，密文接收者会收到密文、IV（计数器CTR的初始值）、MAC值。

填充模式

在前面介绍分组模式时， 讲到 ECB 模式和 CBC 模式是需要对数据块进行填充的。填充机制并没有太多的限制，一种简单的做法是使用 0 值的填充模式。假设分组长度是64比特，明文最后一个分组长度是24比特，可以补充40比特的 0 值，描述如下：

使用0进行填充

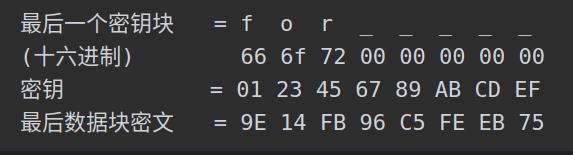
解密后，最后一个明文分组就是66 6f 72 00 00 00 00 00，去除明文末尾的 0 值，就得到原始明文。

但仔细一想，这种填充模式存在问题，如果明文末尾本身就存在 0 值，就有问题。

为此，人们提出了更好的填充方案，并进行了标准化，最常见的两个标准就是 PKCS#7 和PKCS#5 标准。

• PKCS#7

PKCS#7填充标准很简单，先观察如下填充规律：

PKCS#7填充

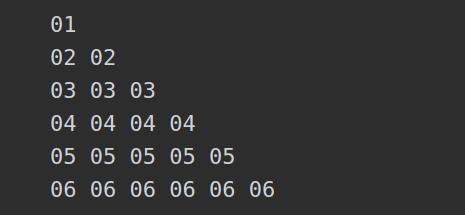
可以看出，其规律是根据填充的字节数量进行对应的填充，如果填充的字节长度 n 是3，填充的值就是030303；如果 n 是5，那么填充的值就是0505050505，填充值最后一个字节代表的就是实际填充的长度。

有人可能会有疑问，要是数据块长度正好是分组长度的整数倍，而且末尾的数据为 01 或 0202 这样的数据呢？对此，参考 RFC 5652 文档，里面对填充进行了详细的说明：

PKCS#7填充

其中 k 为分组长度，lth 表示明文或者密文的长度。可以看出，如果数据块长度正好是分组长度的整数倍，也需要填充一个数据块。

完成解密后，读取解密值的最后一个字节的值 n ，去除最后 n 个字节得到原始明文。

PKCS#5 和 PKCS#7 处理填充机制的方式其实是一样的，只是 PKCS#5 处理的分组长度只能是 8 字节，而 PKCS#7 处理的分组长度可以是1到255任意字节。可以认为 PKCS#5 是 PKCS#7 标准的子集。

需要注意的是，对数据的填充，通常不需要应用程序处理，加密库一般会处理好，应用程序只需调用简单的加解密接口。

SMS4

SMS4 是我国无线局域网标准 WAPI 中所采用的分组密码标准，随后被我国商用密码标准采用，又名SM4。作为我国商用密码的分组密码标准，SMS4 在国内的敏感但非机密的应用领域将会逐渐取代3DES、AES等国外分组密码标准，用于通信加密、数据加密等应用场合。

SMS4 的密钥长度和分组长度均为 128 比特，其设计安全性等同于 AES-128。由于 SMS4 的密钥长度固定为 128 比特，并没有提供更长的可选密钥长度，因此 SMS4 不适用于保护需长期保密的数据，如需 50 年才能解密的保密文档。

SMS4 算法存在一定的性能问题。由于 SMS4 设计时的预计应用领域为低功耗芯片(即 WAPI 芯片)，因此 SMS4 针对减少硬件电路数量进行了优化，带来的后果是 SMS4 的软件实现效率较低，难以充分利用主流 32位/64位 通用处理器的计算能力，其软件实现的效率通常大大低于AES-128的软件实现。

对称加密实践

开源国密库 GmSSL 已经实现如下工作模式：

• SMS4-ECB，该模式不推荐
• SMS4-CBC，该模式的实现提供自动的填充，无需应用对明文数据进行填充。
• SMS4-CFB，根据输出比特序列的长度，包含SMS4-CFB1、SMS4-CFB8和SMS4-CFB128三个实现。
• SMS4-OFB
• SMS4-CTR，由于SMS4软实现性能较低，因此在后续的优化中会首先提供经过Intel AVX2指令集优化的CTR实现。
• SMS4-WRAP，将SMS4用于加密密钥，其中被加密的数据为密钥，而SMS4的密钥为KEK (Key Encryption Key)。

GmSSL提供了命令行工具，调用 SMS4 的命令行例子如下：

$ echo hello | gmssl enc -sms4-cbc > ciphertext.bin
enter sms4-cbc encryption password:********
Verifying - enter sms4-cbc encryption password:********

$ cat cipehrtext.bin | gmssl enc -sms4-cbc -d
enter sms4-cbc decryption password:********
hello

小结

对称加密算法比较容易理解，作为开发者通常也不需要理解算法。但是对密钥长度、分组模式和填充模式需要理解，否则极容易造成安全问题。CBC 模式和 CTR 模式是最常用的两种分组模式，不要选择 ECB 分组模式。填充模式只需做一个简单了解，通常对数据的分组和填充都是在加密库内部处理。

下篇文章将为大家介绍非对称加密算法，敬请关注！