对称加密 2/2
Posted 玄同安全
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了对称加密 2/2相关的知识,希望对你有一定的参考价值。
导语
本文为「小玄同学讲安全」系列文章第四篇,也是对称加密的第二篇。
在这篇文章中我们详细介绍了DES、3DES、AES三种对称加密算法,其中3DES和AES是作为DES的代替者被提出的。实际上,DES不止有这两种代替算法,还有IDEA、RC - 2、RC - 4、RC - 6等等。
因此,本文将介绍IDEA、RC - 2、RC - 4、RC - 6,让大家对对称加密这个大家族有更全面的了解。
一、IDEA
国际数据加密算法(International Data Encryption Algorithm,简称IDEA)是上海交通大学教授来学嘉与瑞士学者James Massey联合提出的。最初,它在1990年以PES的形式发布,两年后改进并更名为IDEA。IDEA弥补了DES密钥太短等缺点,具备更强的安全性。
IDEA属于对称加密的块密码算法,利用128 bits的密钥可将64 bits的明文转换成64 bits的密文。
1.1 加密原理
1.原理综述
每次IDEA加密只能处理64 bits的明文,如果待处理信息超过64 bits,则需分成多个明文块进行多次加密。
每次IDEA加密的过程如下图所示:
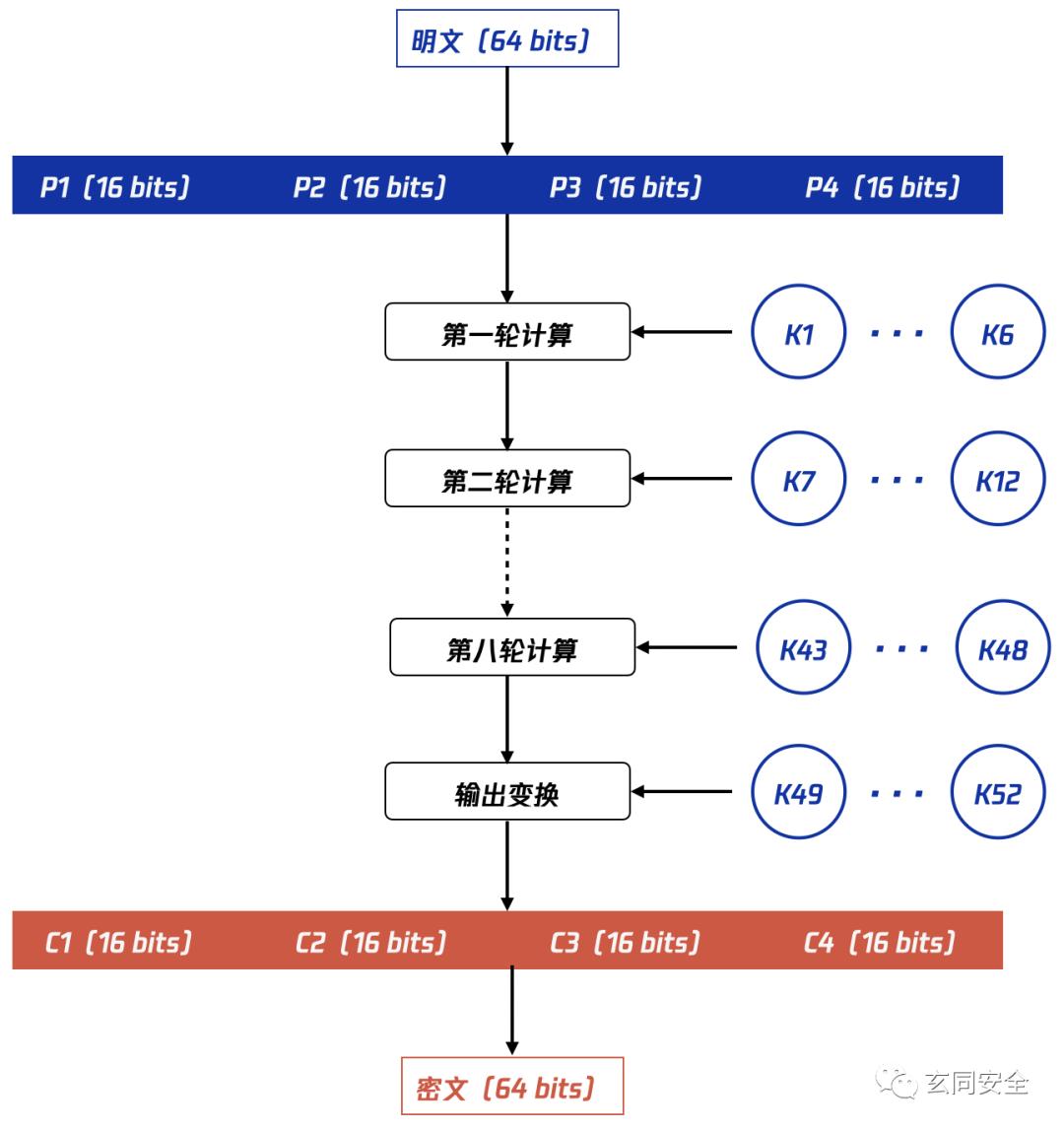
由加密过程图可知,一次IDEA加密需要经历九轮计算,包括八轮原理相同的循环计算和一轮输出变换。加密过程可以概括为以下四个步骤:
①将64 bits明文分为四个16 bits的明文块,记为“P1”、“P2”、“P3”、“P4”;
②将上一步得到的明文块和六个16 bits的子密钥带入到第一轮计算中;
③将上一轮的结果及本轮的子密钥对应带入到第二、三、…、八轮计算中;
④将第八轮的结果及四个16 bits的子密钥带入到输出变换中,以生成四个16 bits的密文块,即为64 bits密文。
需要注意的是,前八轮循环计算需要六个16 bits的子密钥,输出变换需要四个16 bits的子密钥。但是本次加密的原始密钥仅有128 bits。因此为满足子密钥的总位数要求,需要对原始密钥进行处理。详见本节第2部分。
2.子密钥的生成
子密钥的生成原理如下图所示:
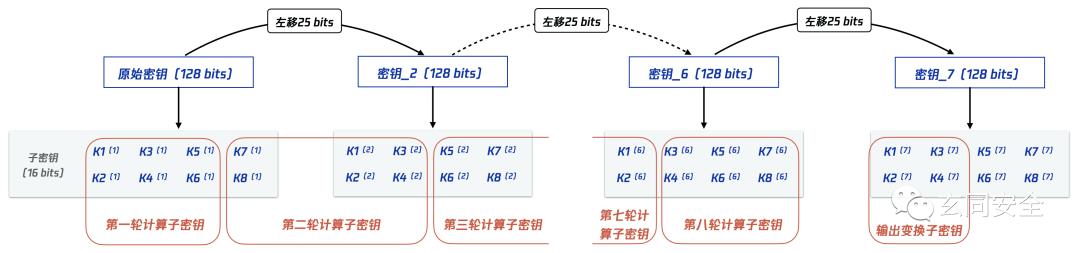
由上图可知,子密钥的生成方法是以原始密钥为基础,通过将其不断左移25 bits以生成新的密钥,然后将原始密钥和新生成的密钥等分为多个16 bits的子密钥,并依次带入到IDEA的加密运算中。具体步骤如下:
①将原始密钥等分为八个16 bits的子密钥,取前六个作为第一轮计算的子密钥;
②将原始密钥左移25 bits得到“密钥_2”,再将密钥_2等分为八个16 bits的子密钥。取第①步的后两个和此步骤的前四个子密钥作为第二轮计算的子密钥;
③以此类推,将密钥_2不断左移25 bits,依次得到“密钥_x”(x = 3、4、…、7)。然后将“密钥_x”均等分为八个16 bits的子密钥,再将子密钥按照顺序带入后续的运算步骤中。
需要特殊说明的是,前八轮计算均需要用到6个子密钥,而最后一步输出变换中仅需4个子密钥。因此由“密钥_7”得到的后四个子密钥直接丢弃就好。
3.前八轮计算原理
IDEA加密中前八轮计算的原理均是相同的,每轮的计算步骤如下:
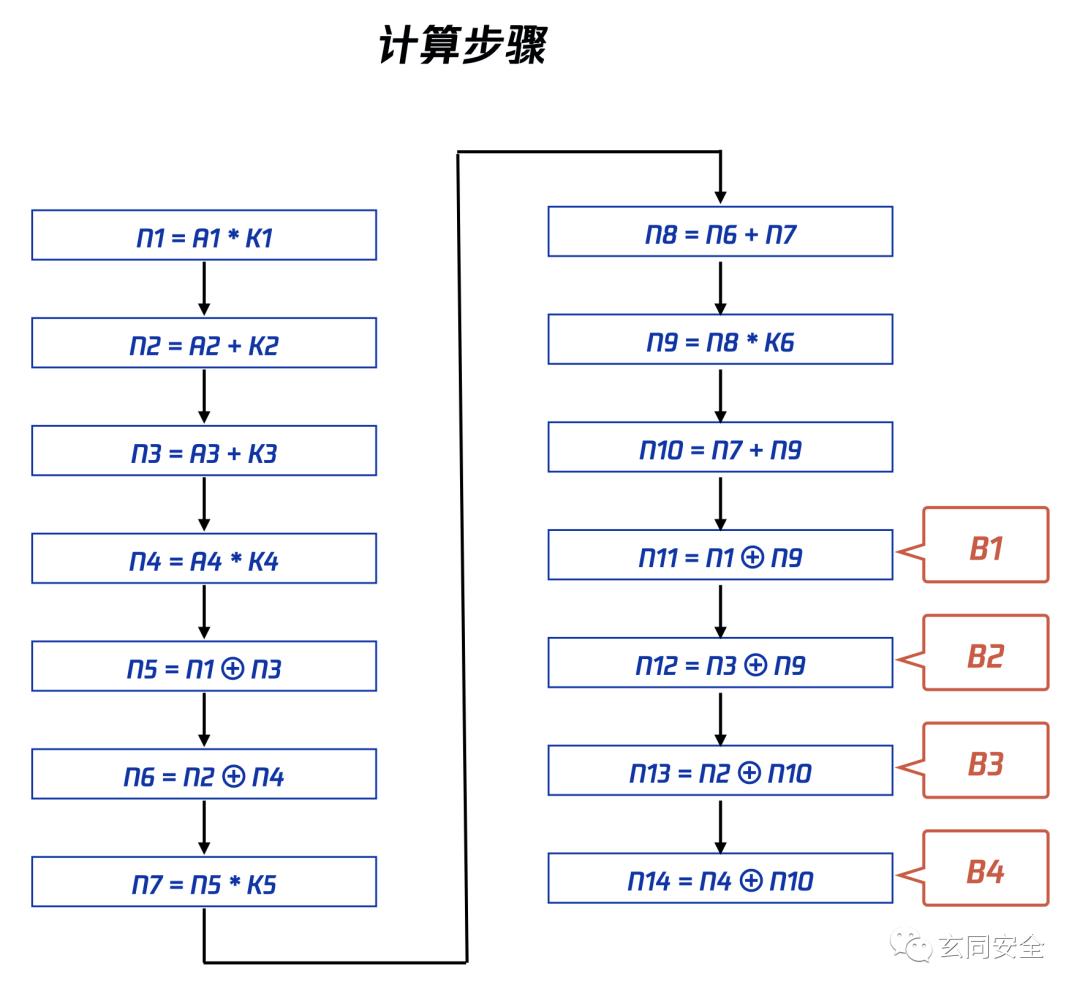
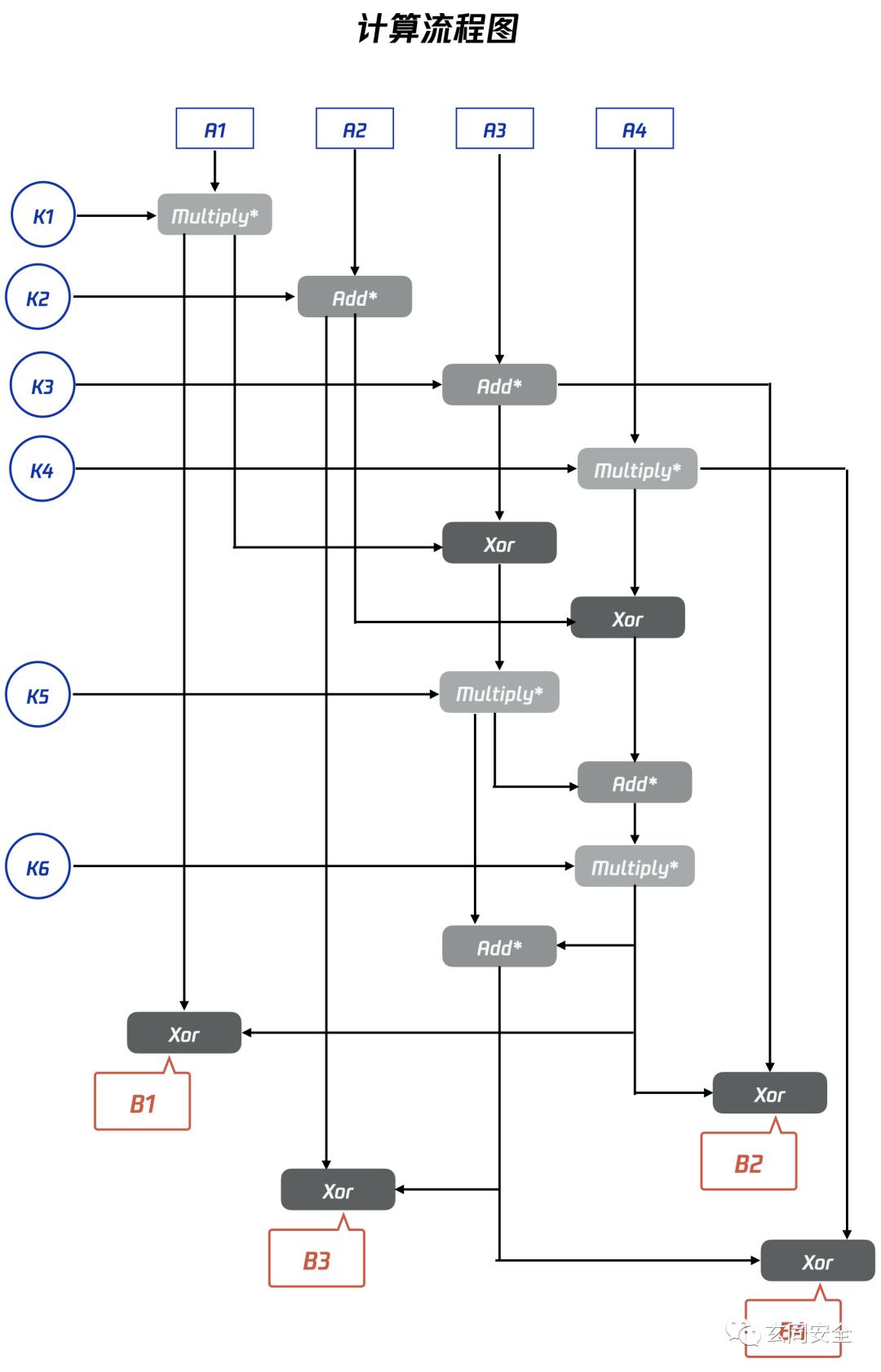
在以上计算步骤中,我们用A1、A2、A3、A4分别表示每轮计算的四个输入块(16 bits),它们可能是明文块,也可能是上一轮计算的结果( 需将上一轮计算输出块的第2、3块互换,才能作为本轮的输入;最后一轮除外);用N1、…、N14表示每个步骤的计算结果;用K1、…、K6表示本轮计算的子密钥;用B1、B2、B3、B4表示本轮计算的输出块。
由图可知,我们通过相加(+)、相乘(*)、异或(⊕)三种运算方法,将输入块和子密钥转化为输出块。但是,在两个16 bits数相加或相乘时,其结果很可能大于16 bits,而我们的结果却要求是16 bits的。那么这是就需要利用求模算法,相加后用2^16求模,相乘后用2^16+1求模,以保证计算后的结果是16 bits的。
4.输出变换原理
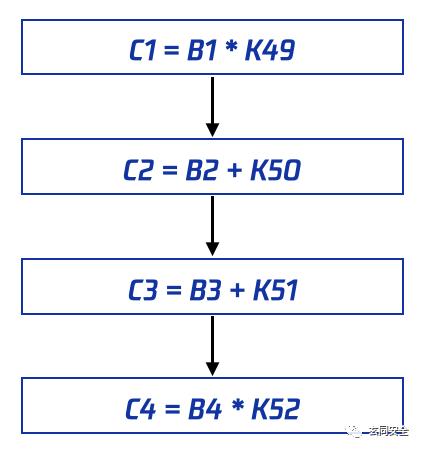
这里,我们用B1、B2、B3、B4表示第八轮计算的输出块(最后一轮的输出块是不需要交换位置的);用C1、C2、C3、C4表示输出变换的结果,同时也是本次IDEA加密的密文块;用K49、K50、K51、K52表示输出变换所需的子密钥。
通过图中的四步计算即可得到最终的密文块,至此也就完成了本次IDEA加密。
1.2 安全性分析
目前来说,针对IDEA算法的最佳公开破解是复杂度为2126.1的Narrow Bicliques的攻击。(具体分析详见:Narrow-Bicliques: Cryptanalysis of Full IDEA)
由于后来被提出的AES算法具备更高的运算效率和安全性,再加上使用IDEA需获得专利许可这个原因,IDEA的使用频率越来越低。
Rivest Cipher(简称:RC)系列的加密算法也是对称加密中比较常见的算法,但它们的使用频率要低于综合性能更强的AES等算法。
接下来的三章会详细介绍RC系列中的RC2、RC4、RC5,其中RC5算法要更常见一些。
二、RC2
RC2是著名密码学家Ron Rivest设计的一种传统对称分组加密算法,它可作为DES算法的建议替代算法。它的明文和密文都是64 bits,密钥的长度是从1字节到128字节可变,1998年的实现是8字节。
2.1 加密原理
1.原理综述
RC2加密是由密钥填充、混合、捣碎这三个核心运算过程组合而成的。具体步骤如下:
①将输入的明文等分为四个16 bits的明文块,记为“R[0]”、“R[1]”、“R[2]”、“R[3]”;②密钥填充;③五轮混合;④一轮捣碎;⑤六轮混合;⑥一轮捣碎;⑦五轮混合;⑧以上的每一轮运算都会生成新的“R[0]”、“R[1]”、“R[2]”、“R[3]”,而生成的最终值即为RC2加密的密文。
下面对密钥填充、混合、捣碎这三个核心运算过程进行说明。
2.密钥填充
(1)符号说明
T —— 输入的密钥长度,单位:字节,1 ≤ T ≤ 128(1998年实现的是T = 8);T1 —— 输入的密钥长度,单位:bit,T1 = 8*T;T8 —— T8 = ( T1 + 7 ) / 8 ;TM —— TM = 255 MOD 2 ^ ( 8 + T1 - 8*T8 );—— 基于以上是关于对称加密 2/2的主要内容,如果未能解决你的问题,请参考以下文章