说说非对称加密

Posted 2021-04-25 随笔风中

    一直以来,"对称加密"、"非对称加密"、"公钥"、"私钥"等这些词汇对很多人来说都是最熟悉的陌生词, 听着熟悉但是从未理解其中要义。最近再次有人问这个问题,索性就把这些东西理顺给大家分享一下，帮有困惑的小伙伴通俗易懂地理解几个概念，最后会举一个非对称加密的例子，更方便你理解非对称加密。

    非对称加密是相对于对称加密而言的。

    对称加密：小A新建了一个秘密文件（嘿嘿），他用WINRAR对文件压缩并加上密码后，放到了百度去上，让小B去下载，同时把密码告诉小B，小B下载文件并用密码解压后，就可以看到文件了。

    缺点是什么呢？密码在传送过程中可能泄密，从而导致秘密大白于天下。（我忽然想到了那个新闻，某局长发微博与情人调情，还约定下午开房！原来他以为微博就他俩能看见呢，没想到被围观了。所以啊，年轻人，来学学加密吧）

    所谓对称就是加密和解密的过程使用的是相同的密钥。

    那非对称加密呢？与对称加密不同,非对称加密算法的加密和解密使用不同的两个密钥.这两个密钥就是我们经常听到的"公开密钥"(公钥)和"私有密钥"(私钥).

    公钥和私钥的关系是:

      公钥和私钥一般成对出现,

      如果你的数据使用公钥加密,那么需要该公钥对应的私钥才能解密；

      如果你的数据使用私钥加密,那么需要该私钥对应的公钥才能解密。

    非对称加密的作用是:保护消息内容, 并且让消息接收方确定发送方的身份。

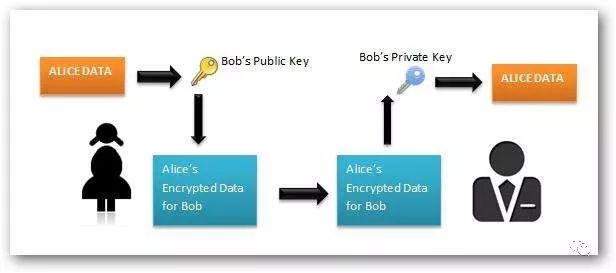
    听起来很神奇的样子是不，但很多人不明白为什么用加密的公钥不能解密呢？

    网上很多文章讲到这里就停住了，你如果想搞明白，就听多慢慢道来。

    

    我们来做个小游戏，你任意想一个3位数，并把这个数和91相乘，然后告诉我积的最后三位数，我就可以猜出你想的是什么数字啦！

    比如你想的是X，乘以91后，把结果的末三位193告诉我。

    看起来，这么做似乎损失了不少信息，让我没法反推出原来的数。感觉三位数乘以91，末三位是193应该有很多啊。

    学过编程的同学可以编个循环把所有三位数试一下，三位数乘以91，末位是193的，只有123。

    当然，我猜出你的数不是用循环，我是把193乘以11，结果是2123，末三位就是想的123。

  

    是不是觉得这方法太LOW啊，别急耐下心来，听我继续说。

    其中的道理是，91乘以11等于1001，而任何一个三位数乘以1001后，末三位显然都不变（例如123乘以1001就等于123123）。

    知道原理后，我们可以构造一个更多位数的，不仅限于三位数。

    比方说，任意一个数乘以400000001后，末8位都不变，而400000001 = 19801 * 20201，于是你来乘以19801，我来乘以20201，又一个不对称加解密的系统就构造好了。91就是公钥， 11就是私钥。

    甚至可以构造得更大一些：4000000000000000000000000000001 = 1199481995446957 * 3334772856269093，这样我们就成功构造了一个30位的加密系统。

    这个位数要多到你用循环去试的话，要很多时间，比如一年、十年等。

   这是一件非常coooooooool的事情，任何人都可以按照我公布的方法加密一个数，但是只有我才知道怎么把所得的密文变回去。其安全性就建立在算乘积非常容易 也很快，但是要把4000000000000000000000000000001分解成后面两个数相乘，在没有计算机的时代几乎不可能成功！

    但如果仅仅按照上面的思路，如果对方知道原理，知道我要构造出带很多0的数，根据19801和8位算法这2个条件非常容易穷举出400000001这个目标值。要解决这个问题，真实世界就不是使用乘法了，比如RSA算法使用的是指数和取模运算，但本质上就是上面这套思想。

    差不多就这样了，你可以继续去快乐的玩微信去了。

如果对RSA感兴趣的，往下看

    

    下面用两个小素数7和17来建立一个简单的RSA算法：

    (1)选择两个素数p=7和q=17；

    (2)计算n=p*q=7*17=119，计算Φ(n)=(p-1)(q-1)=6*16=96；

    (3)选择一个随机整数e=5，它小于96，并且与96互素；

    (4)求出d，使得d*e=1 mod96 且 d<96，此处求出d=77，因为 77*5＝385 对96取余为1；

    (5)假设明文M＝19，计算19模119的5次幂，M的e次方＝19的5次方，结果对119取余,密文C＝66；

    (6)接收密文66，计算66模119的77次幂；C的d次方=66的77方，结果对119取余，19，即得到明文19。

      公钥 e 用来加密，私钥 d 用来解密。