原创 |十分钟读懂加密技术：非对称加密技术

Posted 2021-04-25 南湖互联网金融评论

作者

南湖互联网金融学院 赵伟

非对称加密（公钥加密）指在加密和解密两个过程中使用不同密钥。在这种加密技术中，每位用户都拥有一对钥匙：公钥和私钥。在加密过程中使用公钥，在解密过程中使用私钥。公钥是可以向全网公开的，而私钥需要用户自己保存。这样就解决了对称加密中密钥需要分享所带来的安全隐患。

由于公钥公开，任何用户都可以利用特定用户的公钥，对消息或数据加密保护然后发送给该用户。收到消息后，该用户利用独有的私钥对接收到的内容进行解密，以获取信息。由于除了该用户之外，没有其他用户拥有能够对该密文解密的私钥，因而该密文对其他用户来说都是不可读的。这样就能让收发双方放心地将加密消息或数据在网络传播。通过共享私钥来建立信息通道的方式不再是必要的，用户拥有的一对公钥和私钥就是安全的信息通道保障。

非对称加密技术能够实现并且能够保证安全的关键是任何人利用公开的公钥在操作上不太可能推导或计算出该用户的私钥。注意，这里指“在操作上（主要指利用计算机进行计算）不太可能”，并不意味着在理论上绝对不可能。事实上，我们可以假设存在这样一个程序，能够轻松地解决这样的逆运算问题，只是没有人知道如何构造这样的程序。

一、陷门函数

陷门函数是有陷门的特殊单向函数，即从X向Y计算非常容易，但在没有特定信息的情况下，从Y计算X非常困难[1]。陷门函数也可类比为和面，从面粉到面团的方向是容易的，只需要将面粉和适量的水混合，加以揉搓便可以得到面团，但是从相反的方向，将面团变成面粉和水就有很大难度。理论上，完美的陷门函数是否存在还没有得到证明。但是从密码学的角度上看，只要逆运算“困难”到一定程度，就能利用这个性质构造密码算法[2]。

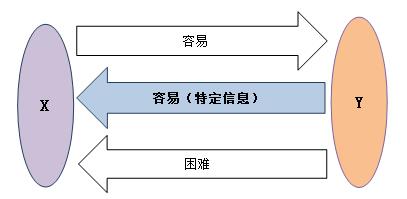
图1  陷门函数

公钥加密利用的就是这类函数的特性，可以把私钥理解成上图的X，公钥是上图的Y，每位用户利用自己的私钥X，利用陷门函数来生成自己的公钥Y，并向全网公开公钥，这样每位用户都有一对钥匙，不必担心公开公钥会泄露私钥。

具有这种特性的数学问题有很多，下文以椭圆曲线上的离散对数问题为例展开介绍。

二、公钥密码体制

椭圆曲线问题的研究已经有了上百年的历史，有着丰富的研究内容，而离散对数问题一直都是数学界的一个难题，目前世界上并没有快速求解离散对数的方法。下面以尽可能浅显易懂的语言介绍如何利用椭圆曲线的离散对数问题来构建公钥密码体制。

试想这样一种情景，你的朋友约你去打台球，但他/她比你早到一个小时，并且先开始用白球击打黑球，假设台球桌上没有其他球，也没有可以得分的洞，两个球始终都只在球台表面移动。你的朋友在一个小时的时间里做的事情就是不断用白球击打黑球（击球的频率没有规则，他/她可以在任何时候停下来休息）。等你到了之后，你的朋友告诉你黑球刚开始的位置以及黑球现在的位置，让你根据这两个位置的信息，推测出黑球共被击打了多少次？

如果再将上面情景的一个小时换成一天或者一个月，又或者根本就不知道击球时间呢？很显然对于上述情景，想要回答出问题只能是不停地猜测这个次数。而当这个次数的正确答案在一个巨大的范围内时，实际上能够正确回答这个问题的可能性几乎为零[3]。基于椭圆曲线的离散对数问题的公钥加密机制跟上述问题十分相似。

椭圆曲线的图像并不是一个椭圆，其名字的由来是因为这个问题始于对椭圆周长的研究。下面用一个例子[4]来说明椭圆曲线的图像以及其如何用来建立公钥加密体制。

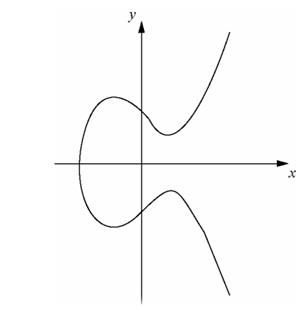
图2  实数上的椭圆曲线图像

上图是椭圆曲线一般形式的一种，可以看出这个图像关于轴对称，不同的椭圆曲线的方程参数取值不同会使得其形状也不一样，但是这个对称性质不变。在密码学的应用上，椭圆曲线的真实图像是由坐标上的点构成，并且这些点被包含在一个有限空间内，参数的作用可以简单理解为实际算法中使用到的椭圆曲线上的点的个数。调整椭圆曲线的参数可以改变有限空间[5]的大小（可以将参数的作用理解为能够控制台球情景中台球桌的大小），后文将会详细介绍参数。

回想一下打台球的情景，现在把这个椭圆曲线的图像想象成球台，接下来就开始介绍在椭圆曲线上的“击球”过程。在椭圆曲线上的“击球”和在球台上的击球过程类似，是将曲线上的一个坐标点移动到另外一个坐标点（击球时是将球在一个位置移动到另一个位置）。这个操作在椭圆曲线叫做“加”。

接下来就开始介绍在椭圆曲线上的“击球”过程。在椭圆曲线上的“击球”和在球台上的击球过程类似，是将曲线上的一个坐标点移动到另外一个坐标点（击球时是将球在一个位置移动到另一个位置）。这个操作在椭圆曲线上叫做“加”。

“加”的操作有两种，第一种是不同的两个点相“加”，第二种是相同的点相“加”，这里采用的是同点相“加”。假设坐标点的起始点是P点（球的起始点），经过一次“加”（一次击球）：P+P，得到2P：在图像中的P点处画一条经过P点的切线，这时候会得到切线与椭圆曲线的第二个交点，而这个交点的关于X轴的对称点2P就是经过一次“击球”的球的位置，如图3。

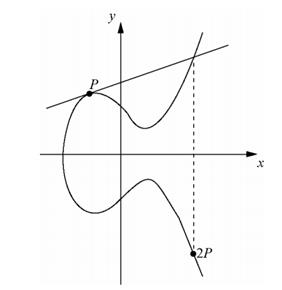
图3  椭圆上的同点相“加”

第二次的“加”操作也和之前一样，在2P点做一条切线，然后取这条切线与椭圆曲线的交点关于X轴的对称点，得到3P点。经过n-1次“加”的操作，最后得到的点为终止点（停止击球后，球在球台的最后位置），为了方便称之为Q点，所以：Q=nP，这里的Q和P是坐标上的点，而n则是一个常数。

在这个加密体制中，P和Q就是公钥，而n则是私钥。回想一下台球的情景，球的起始位置和最终位置就相当于是椭圆密码体制里的公钥，而击球次数则是坐标点的操作次数，也就是私钥。基于椭圆曲线的离散对数问题的特性，使得在知道私钥n的情况下非常容易计算出Q，但是相反，在知道P和Q的情况下却难以反推出私钥n。

参数的另外一个作用是调整这种加密技术的安全性，参数的范围越大，可“加”的次数也就越多，猜中或者计算出真实的私钥（n）的可能性就越低，使得加密技术的安全性越高。

基于椭圆曲线问题的加密算法还具有效率高，速度快，省算力的特点，因而被广泛地运用于网络中。事实上，比特币中的加密技术运用的就是这个机制。

注释

[1]这里的“容易”和“困难”指的是在实际操作过程中的难易。

[2]郑东.密码学.第2版[M].电子工业出版社,2014.

[3]理论上能找到正确答案，因为不论是一个月还是一年，击球的次数始终有限，会是一个存在的整数，如果你能够从1开始不断地猜测，理论上总有一天你能猜对正确答案。但是如果花费的时间是一百年、一千年甚至更多时，那这个正确答案显然没有什么意义，所以在实际操作中把这样的情况可以归为不可能回答得出正确答案。

[4]这里只是椭圆曲线参数取值的一个情况，并且文中没有给出椭圆曲线的定义以及一般形式，有兴趣的读者可以阅读2007年由科学出版社出版的《椭圆曲线及其在密码学中的应用》，作者为恩格。

[5]这里涉及到群的知识，本文不做深入。有兴趣读者可参见“The Arithmetic of Elliptic Curves”，作者 Silverman J H。

（完）

 -------------分割线-------------

或长按并识别以上二维码，关注NIFIReview

学院网站：www.nifi.org.cn

更多学术报告，尽在NIFI。