TLS/SSL 协议-非对称加密(RSA)原理

Posted 2021-04-25 爱因诗贤

关注爱因诗贤

每天进步一点点

导读

前面文章学习过 对称加密的原理，在通信双方发送完加密的密文之后，需要发送密钥给对方才能解密，这就要求发送密钥的信息通道安全可靠，才能保证数据的安全性，而非对称加密算法 是一种密钥的保密方法，需要有公钥(公开密钥）和私钥（私有密钥），这篇文章主要介绍公钥和私钥生成原理，然后围绕公钥和私钥研究和分析一下加密是如何起到密钥保密作用的。

1.非对称加密的工作原理

• （1）Bob要向Alice发送信息，Alice需要先要产生一对用于加密和解密的公钥和私钥。

• （2）Alice的私钥保密，Alice的公钥告诉Bob。

• （3）Bob把要发送的信息用Alice的公钥加密生成密文发送给Alice。

• （4）Alice收到这个消息后，用自己的私钥解密Bob的消息。其他所有收到这个报文的人都无法解密，只有Alice私钥才能解密此信息。

  
  

  Tips：Alice 向 Bob 发送信息时也是同理，Bob 也需要生成一对公钥和私钥。

2.非对称加密和解密过程示意图

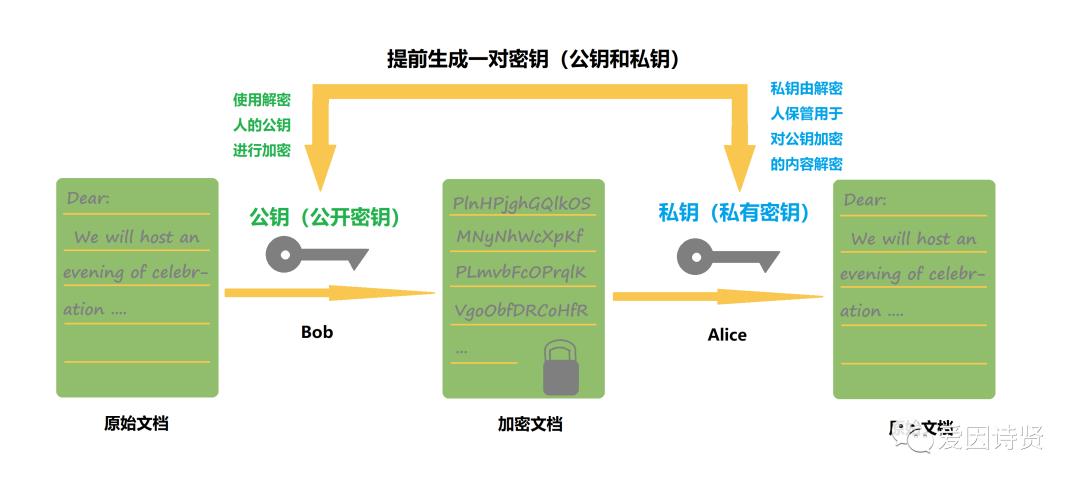
3.RSA 算法介绍

1977 年由罗纳德·李维斯特（Ron Rivest）、阿迪·萨莫尔（Adi Shamir）、伦纳德·阿德曼（Leonard Adleman）一起提出，因此命名为 RSA 算法：

3.1 RSA 算法生成公钥和私钥原理

• （1）随机选择两个不相等的质数 p 和 q。

• （2）计算 p 和 q 的乘积 n（明文小于 n）。

• （3）计算 n 的欧拉函数 v=φ(n)。

• （4）随机选择一个整数 k（1 < k < v，且 k 与 v 互为质数）。

• （5）计算 k 对于 v 的模反元素 d。

• （6）公钥：（k，n）。

• （7）私钥：（d，n）。

• Tips:如果两个正整数 a 和 n 互质，那么一定可以找到整数 b，使得 ab-1 被 n 整除，或者说 ab 被 n 除的余数是 1,此时，b 就叫做 a 的模反元素。

• 3.2 RSA 算法加解密流程

下面以加解密一个数字 123 为例，公钥是 (3,319)，密钥是 (187,319)：

• （1）加密：c = （m^k）mod n，其中 m 是明文，c 是密文，公钥是 k 和 n，即 c = (123^3) mod 319 =140。

• （2）解密：m = (c^d) mod n，其中 m 是明文，c 是密文，私钥是 d 和 n，即 m = (140^187) mod 319 = 123。

• 4.基于 openssl 生成的公钥和私钥

• 首先需要在 Linux 上安装一个 openssl，安装成功之后可以使用 openssl version -a 查看 openssl 版本信息，如下：

• 

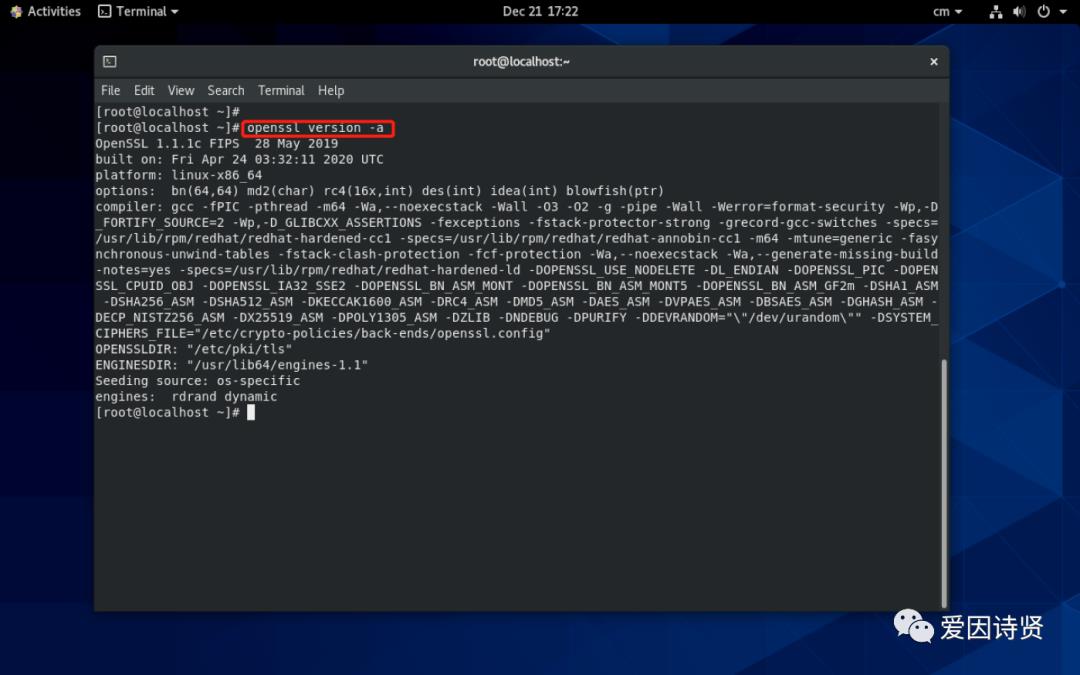
• 4.1 生成私钥

• 
  

• 生成私钥的命令如下：

• openssl genrsa -out private.pem

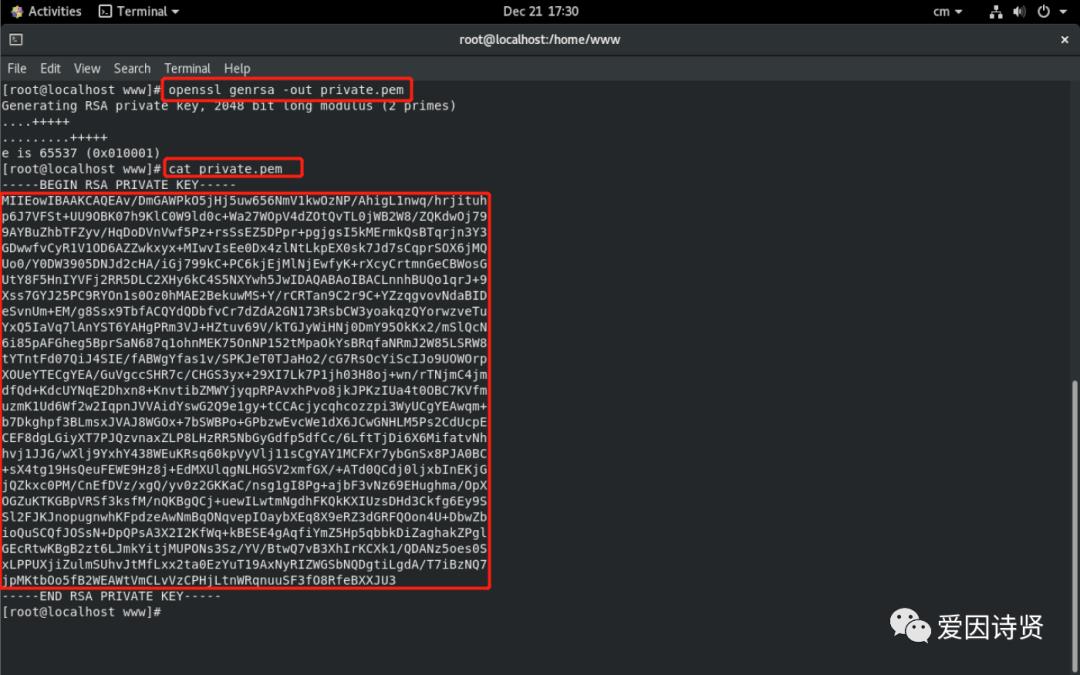
• Tips：openssl genrsa -out private.pem 命令中的 -out private.pem 表示将生成的密钥保存到 private.pem 文件中。

•  4.2 创建一个明文文件

• 
  

• 使用 vim test.txt 命令创建一个明文文件，内容如下：

• 关注爱因诗贤，每天进步一点点!

• 4.3 生成公钥

• 
  

• 公钥可以由上面生成的 私钥 中提取出来，命令如下：

openssl rsa -in private.pem -pubout -out public.pem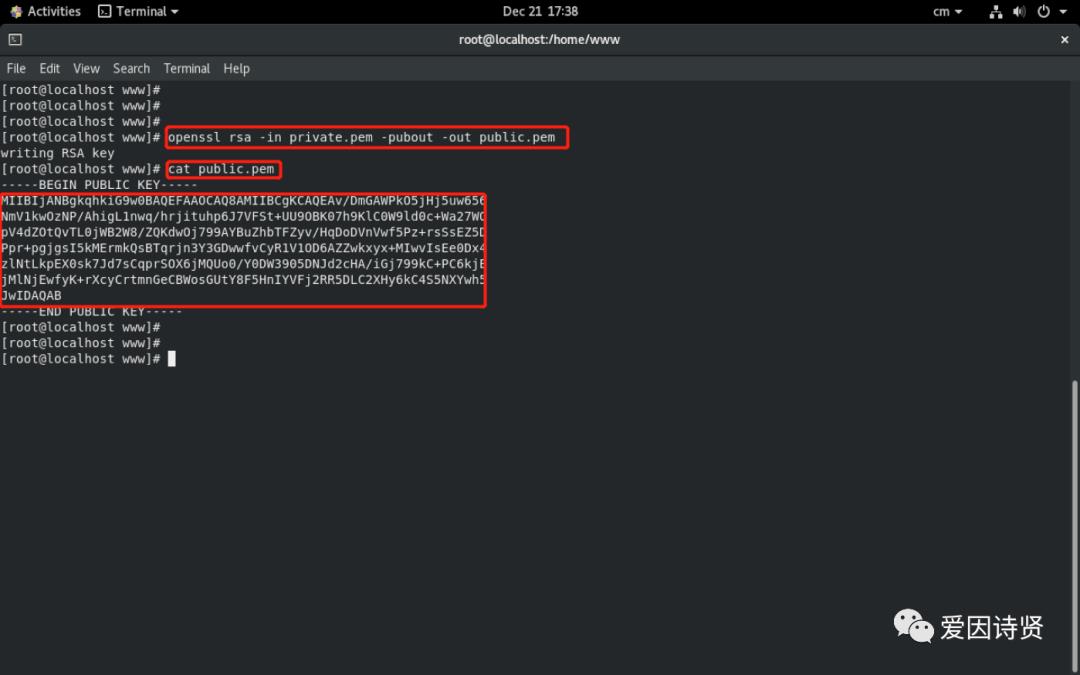

• Tips：openssl rsa -in private.pem -pubout -out public.pem 命令中的 -in 表示输入 priviate.pem 文件内容，-out public.pem 表示将公钥输出到 public.pem 文件中。

• 4.4 RFC3447 文档定义的私钥格式

RSAPrivateKey ::= SEQUENCE { version Version, modulus INTEGER, -- n publicExponent INTEGER, -- e privateExponent INTEGER, -- d prime1 INTEGER, -- p prime2 INTEGER, -- q exponent1 INTEGER, -- d mod (p-1) exponent2 INTEGER, -- d mod (q-1) coefficient INTEGER, -- (inverse of q) mod p otherPrimeInfos OtherPrimeInfos OPTIONAL }

• 4.5 RFC3347 文档定义的公钥格式

RSAPublicKey ::= SEQUENCE { modulus INTEGER, -- n publicExponent INTEGER -- k}

• 4.6 查看 ASN.1 格式的私钥

私钥是基于 ASN.1 格式进行编码的，可以使用 openssl asn1parse -i -in private.pem 命令查看 ASN.1 格式的私钥信息,如下图所示:

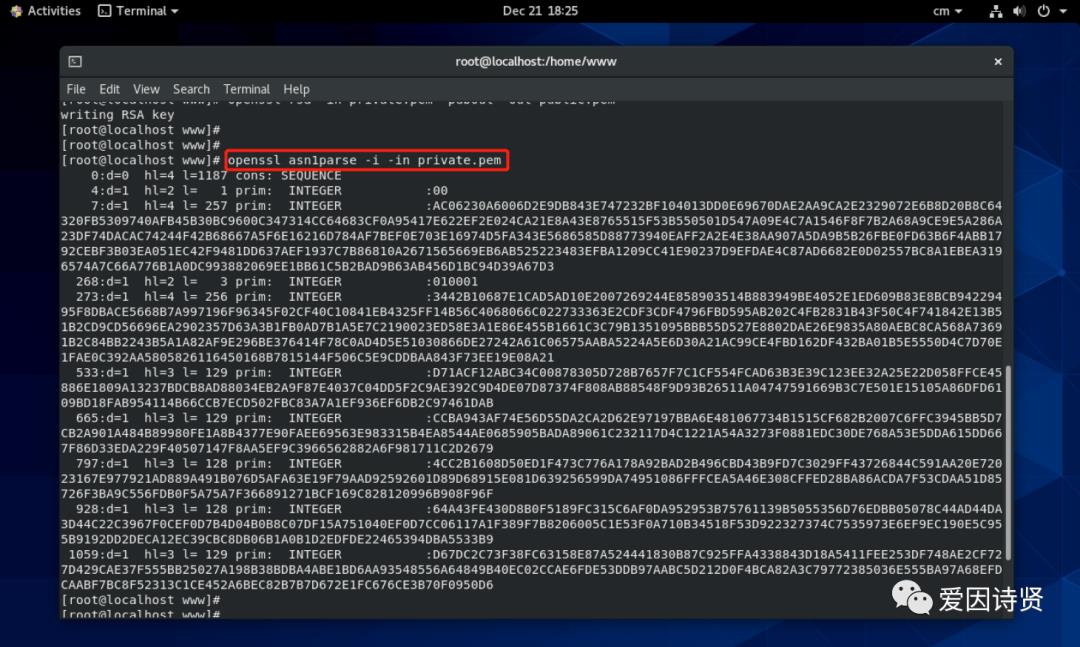
• 4.7 密钥内容格式解析

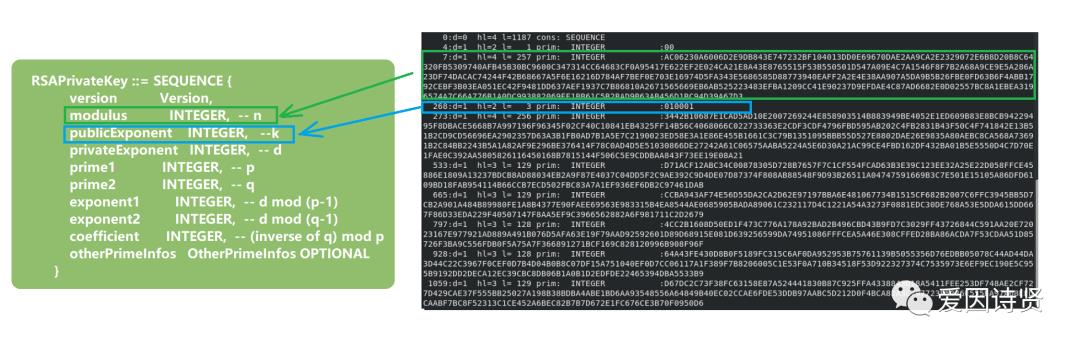
• Tips：--n 和 --k 对应着前面加密流程中的 n 和 k，图中 n 的值是 AC06...6703，k 的值是 010001。

•  4.8 查看 ASN.1 格式的公钥

使用 openssl asn1parse -i -in public.pem 可以查看到如下信息：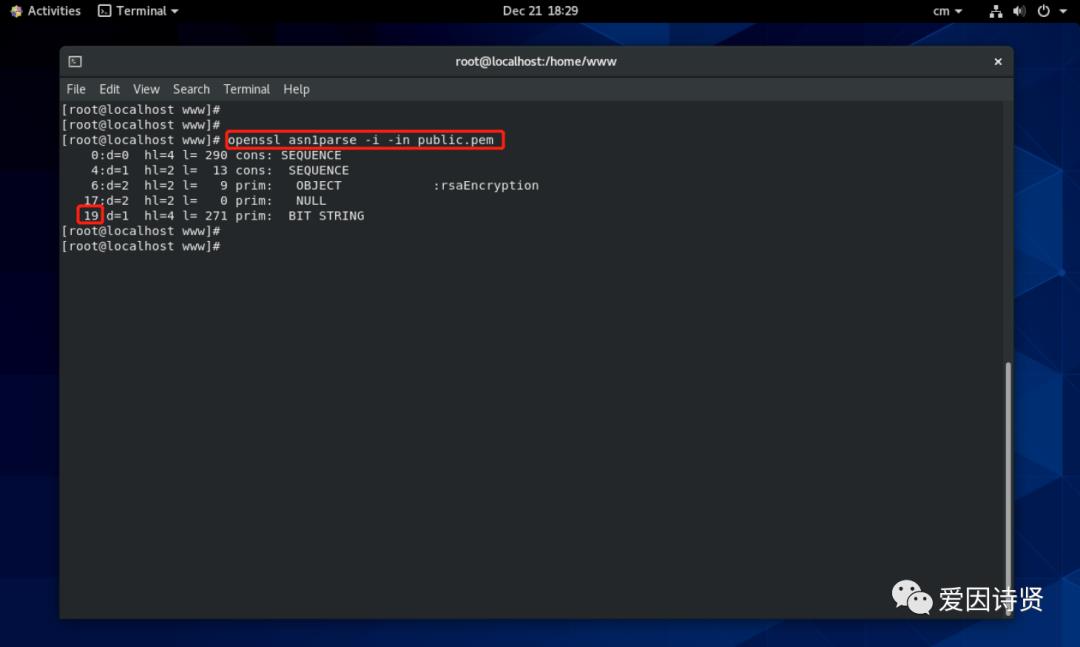

然后使用 openssl asn1parse -i -in public.pem -strparse 19 命令可以查看到公钥的内容如下：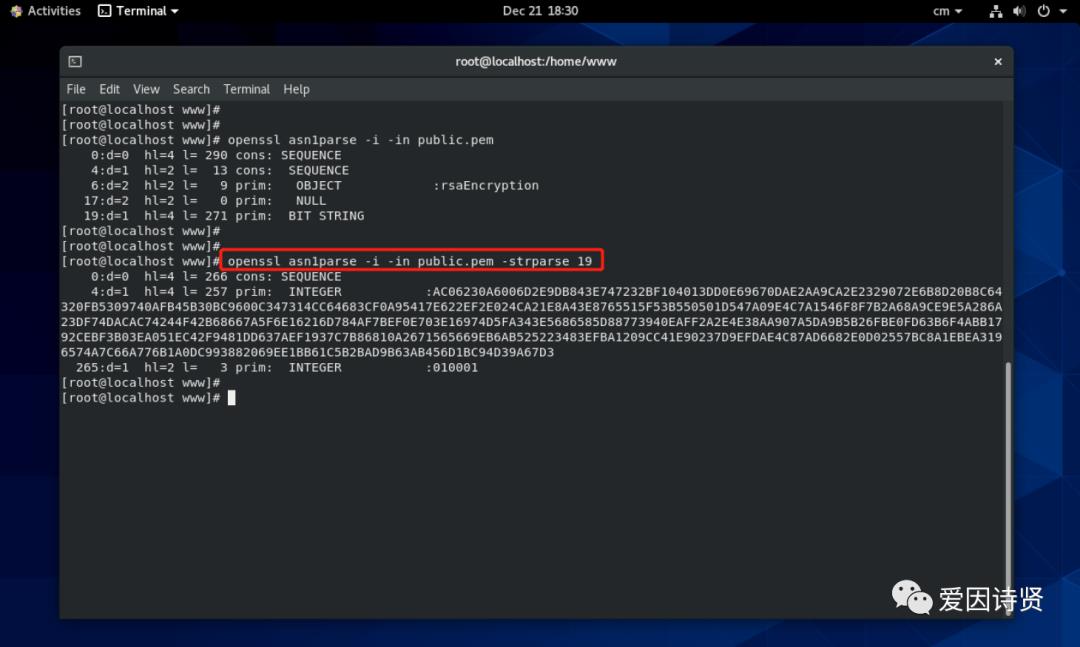

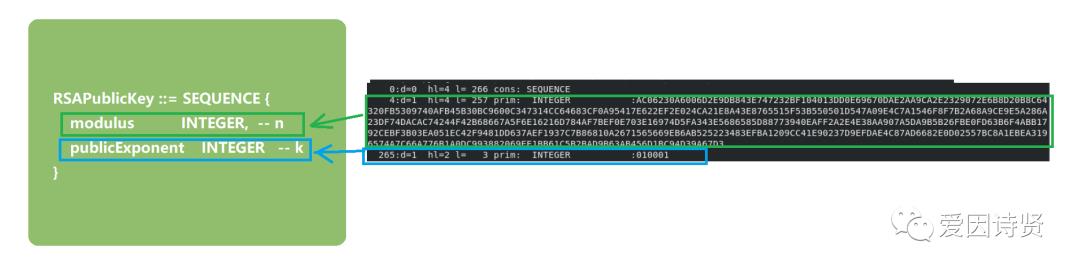
•  4.9 公钥内容格式解析

• Tips：可以对比一下私钥格式化内容和公钥格式化内容，两者是一致的，由此可见，公钥可以由私钥推到出来，反过来则比较困难。

• 4.10 使用公钥对明文加密

使用 openssl rsautl -encrypt -in test.txt -inkey public.pem -pubin -put test.en 可以将前面创建的 test.txt 文件生成密文 test.en 如下图所示：

• Tips：test.en 是生成的密文。

• 4.11 使用私钥对密文解密

使用 openssl rsautl -decrypt -in test.en -inkey private.pem -out new.txt 可以将密文 test.en 解密出来如下图所示: