Holt-Winters -- Kibana5.4时间序列分析

Posted 2021-04-21 bytebees

时序分析   指数平滑   .holt()   

引言

timelion是Elastic公司在ES 2.0提供了pipeline aggregation特性之后推出的实验室产品；最终在5.0版本中，timelion成为Kibana默认分发的一个插件。timelion支持的请求函数包括可视化效果、数据运算、逻辑运算等功能，其中数据运算中的.holt()函数让人格外惊喜——这也是我接触的第一个时间序列分析算法。虽然文档对此函数的预测能力用了"like everything, this is crappy at predicting the future"来形容，.holt()仍不失为一种好的时间序列预测手段，另外也能作为一种异常点检测方法使用。

为避免公式编辑，文中用y^(x+1)表示第x+1个预测值，y(x)表示第x个原始值，0.8**k表示0.8的k次方

准备知识

为了解释三次指数平滑，我们从最简单的概念开始，循序渐进地进行介绍。

时间序列和预测

【序列】就是一列有顺序的数字，为了便于理解，我们可将序列看成具有x和y两个坐标轴的一个二维列表，其中x表示某种顺序，y表示对应点的数值；时间序列就是将时间作为x坐标的序列。所谓【预测】，是根据已知数据（观察值）估算未知数据（预测值）的方法；比如给定一个序列[1,2,3]，y^(x+1)=y(x)+1就是一种预测方法的数学表达。

误差

这段比较无聊，只是想了解原理而不做实践的可跳过。 
很多时候我们会对已经发生的观察值进行“预测”，这时候的观测值也就是原始值，预测值也就是拟合值，他们之间的“距离”可作为判断原始值是否异常的依据。这种“距离”就是误差，因为二者直接做差有可能得到负值，所以一般用下面几种方法来衡量。 
SSE -- 计算的是原始数据和拟合数据对应点的误差平方和；一般SSE越接近0表示模型的选择和拟合更好。下面的MSE和RMSE如出一辙。 
MSE -- 计算的是原始数据和拟合数据对应点误差的平方和均值，也就是SSE/n，n是数据点的个数。 
RMSE -- 回归系统的拟合标准差，是对MSE开平方求得。 
确定系数 -- 上面三种都是点对点求误差的方法，确定系数则是对拟合数据与原始数据均值的差做计算得到的，所以确定系数是通过数据的变化来衡量一个预测模型的好坏。首先是计算SSR，也就是预测数据点和原始数据均值之差做平方和；然后是计算SST，是原始数据点和原始数据均值之差的平方和。确定系数R-Square=SSR/SST，它的取值范围是[0,1]，值越接近1，表示模型拟合的越好。 这类指标是模型调参的依据。

移动平均

不管什么样的序列，都有很多种预测方法，比如y^(x+1)=y(x)就是最简单的一种（认为下一个点的值和当前值一样），再比如y^(x+1)=avg(y(x))，是将序列的均值作为下一个点的预测值（这应该就是统计学中【期望】的来历吧~）。 

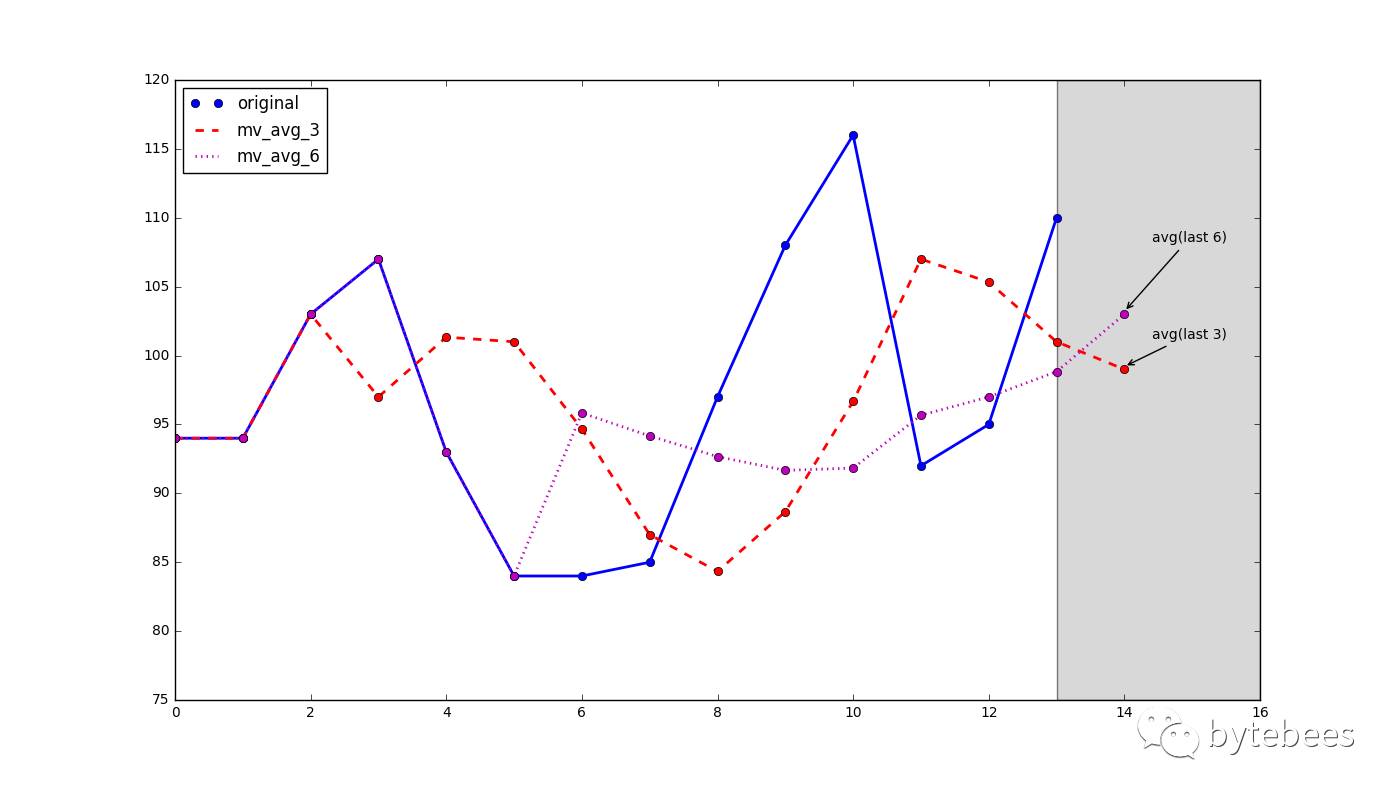
timelion中提供了这样两个函数，.mvavg()和.movingaverage()，称为【移动平均】。移动平均的想法是认为只有最近的数值对预测值才有影响，所以这里面用到了一个参数值n，称为时间窗，计算时只对时间窗里的n个数做平均即可。此外，稍微高级一丢丢的做法是加权移动平均，也就是对时间窗中的每个点单独附一个权重。

对于一个时间序列，我们取不同的时间窗n做移动平均。

def mv_avg(datalst, n):
    mv_avg_data = datalst[:n]
        for k in range(n,len(simple_data)+1):
            mv_avg_data.append(stat.mean(simple_data[k-n:k]))
    return mv_avg_data

Holt-Winters

指数平滑

在做加权移动平均时，沿着这个思路考虑：认为离着预测点越近的点，作用越大。比如我这个月体重100斤，去年某个月120斤，显然对于预测下个月体重而言，这个月的数据影响力更大些。假设随着时间变化权重以指数方式下降——最近为0.8，然后0.8**2，0.8**3…，最终年代久远的数据权重将接近于0。然而这种方式所附权重之和并不为1，所以我们采用一种形式更简单的方式来做：

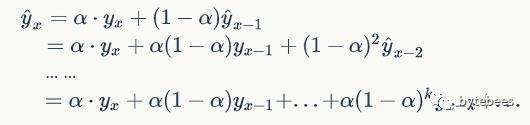
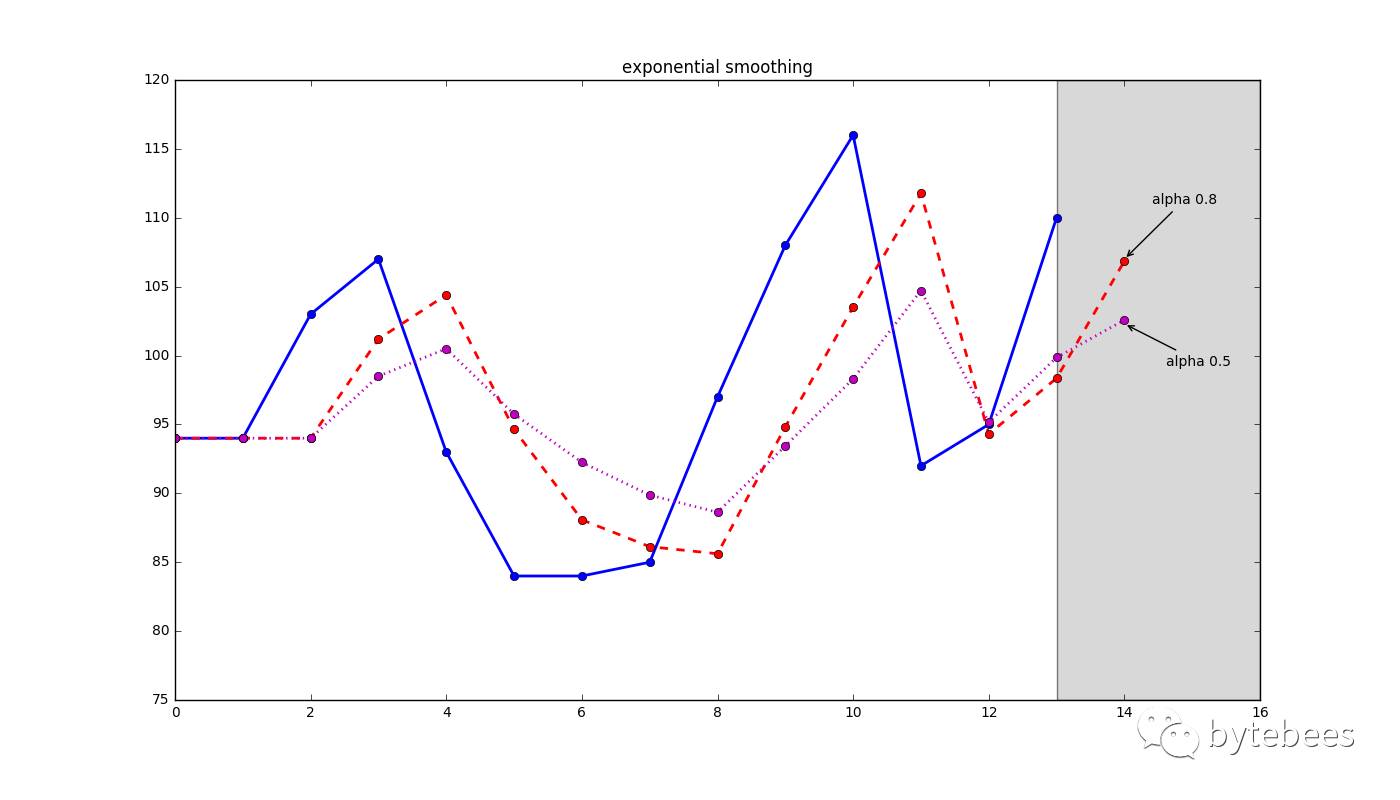
这里的α称为平滑因子，表示我们赋给的最近值的权重，取值为0到1。称α为记忆衰减因子可能更合适——因为α的值越大，模型对历史数据“遗忘”的就越快。由上面的递归展开式可以看到，这种加权移动平均的权重值是指数下降的；另外，这种方法拟合的结果一般而言会比原始数据更加平缓，这也就是【指数平滑】名称的来历。

def exp_smooth(datalst, alpha):
    result = [datalst[0]]
    for k in range(len(datalst)):
        result.append(alpha * datalst[k] + (1-alpha) * result[k-1])
    return result

二次指数平滑

在介绍二次指数平滑前介绍一下趋势的概念。 

趋势，或者说斜率的定义很简单：b=Δy/Δx，其中Δx为两点在x坐标轴的变化值，所以对于一个序列而言，相邻两个点的Δx=1，因此b=Δy=y(x)-y(x-1)。 
除了用点的增长量表示，也可以用二者的比值表示趋势。比如可以说一个物品比另一个贵20块钱，等价地也可以说贵了5%，前者称为可加的（addtive），后者称为可乘的（multiplicative）。在实际应用中，可乘的模型预测稳定性更佳，但是为了便于理解，我们在这以可加的模型为例进行推导。 
指数平滑考虑的是数据的baseline，二次指数平滑在此基础上将趋势作为一个额外考量。用公式来表示就是：

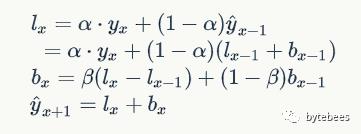
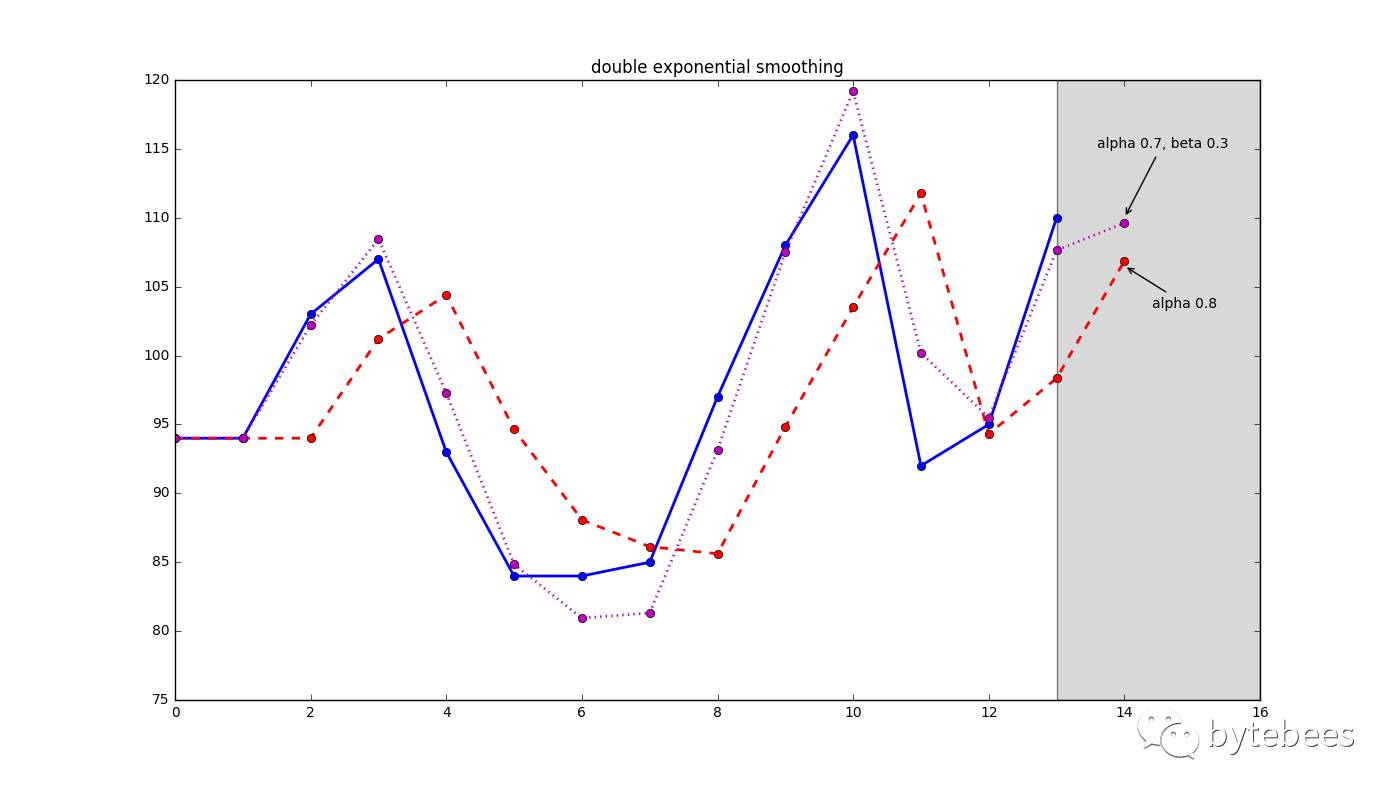
上述第一个式子和指数平滑中的一样；第二个式子中的β称为趋势因子。取β=0.3，α=0.7对同一组数据做预测得到：

def double_exp_smooth(datalst, alpha, beta):
   result = [datalst[0]]
   for n in range(1, len(datalst)+1):
       if n == 1:
           level, trend = datalst[0], datalst[1] - datalst[0]
       if n >= len(datalst): # we are forecasting
           value = result[-1]
       else:
           value = datalst[n]
       last_level, level = level, alpha*value + (1-alpha)*(level+trend)
       trend = beta*(level-last_level) + (1-beta)*trend
       result.append(level+trend)
   return  result

三次指数平滑

三次指数平滑就是Holt-Winters方法，不用说，它的提出肯定是和两个叫Holt和Winters的人有关了。 

当一个序列在每个固定的时间间隔中都出现某种重复的模式，就称之具有季节性特征，而这样的一个时间间隔称为一个季节。一个季节的长度L为它所包含的序列点个数。 
二次指数平滑考虑了序列的baseline和趋势，三次就是在此基础上增加了一个季节分量。比如预测下一个季节第3个点的季节分量时，需要指数平滑地考虑当前季节第3个点的季节分量、上个季节第3个点的季节分量...等等。详细的有下述公式：

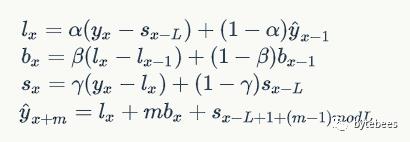
公式中出现了第三个参数γ，γ称为季节平滑因子。此外，预测公式里m可以是任意正整数，而不仅仅是1，这意味着理论上三次指数平滑可以预测未来任何一个时间的值。 
在二次指数平滑中，趋势b的初始值可以通过序列的前两个值简单得到，而Holt-Winters中因为有了多个季节可以得到更好的趋势初始值。关于趋势和季节的初始值我们将在后续讲时间序列分解的时候提到。 
需要注意的是，只有当序列具有季节性时，才能对其采用三次指数平滑方法做分析预测。

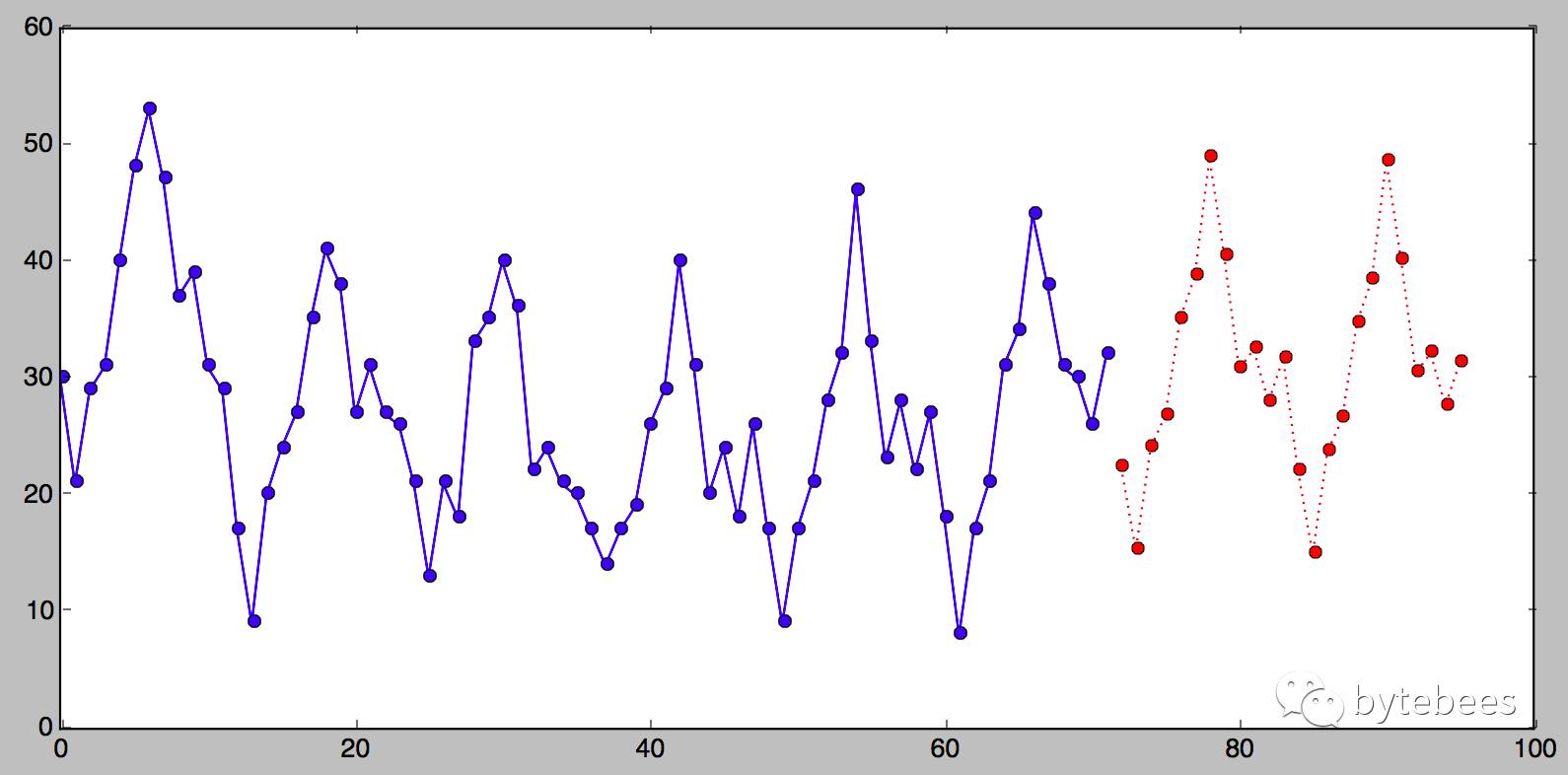
补充两点

异常点监测

Kibana5.4提供的机器学习算法中，有一项异常点检测。虽然并没有看过它的源码，但是我发现Kibana的效果图和我之前用facebook的预测算法做的结果类似，所以估计二者应该有一定的相似性。

facebook发布的这个时间序列预测算法可以很好的拟合以年或者星期为季节的数据，每天一个数据点。为了对我们的交易数据能够以天作为季节做预测，我在代码中添加了分钟、小时的傅里叶级数，这样就可以实现各种不同度量做季节的预测了。万变不离其宗，这种时间序列的预测和Holt-Winters有很多共通之处，有兴趣同学可以看它的源码。

参数选择

Holt-Winters的季节长度可以通过观察获得，而参数α、β、γ就不那么容易确定了。在准备知识中我们介绍了几种误差的计算方法，可以用它们作为衡量拟合效果的函数。所以在实际操作中，类似机器学习中的训练数据和测试数据，可以采用交叉验证的方法对模型进行训练，得到误差最小的参数值。 
介绍完了Holt-Winters方法，留下一个问题思考：时间序列预测和回归的区别是什么。和时间序列的分解一样，这个问题我们将在Kibana5.4时间序列分析(三)中进行更多讨论。敬请关注~

参考：https://grisha.org/blog/2016/02/17/triple-exponential-smoothing-forecasting-part-iii/