常用算法及其Python实现

Posted 2021-04-20 编程面试宝典

技术文章第一时间送达!

冒泡排序

def bubble_sort(li):
    for i in range(len(li)-1): # i表示第几趟
        for j in range(len(li)-i-1): # j表示图中的箭头
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]

============冒泡排序(优化)============
def bubble_sort_1(li):
    for i in range(len(li)-1): # i表示第几趟
        exchange = False
        for j in range(len(li)-i-1): # j表示图中的箭头
            if li[j] > li[j+1]:
                li[j], li[j+1] = li[j+1], li[j]
                exchange = True
        if not exchange:
            return

选择排序

def select(li):
    for i in range(len(li)):
        # 第i趟开始时 无序区：li[i:]
        # 找无序区最小值，保存最小值的位置
        min_index = i
        for j in range(i + 1, len(li)):
            if li[j] < li[min_index]:
                min_index = j
        li[min_index], li[i] = li[i], li[min_index]

插入排序

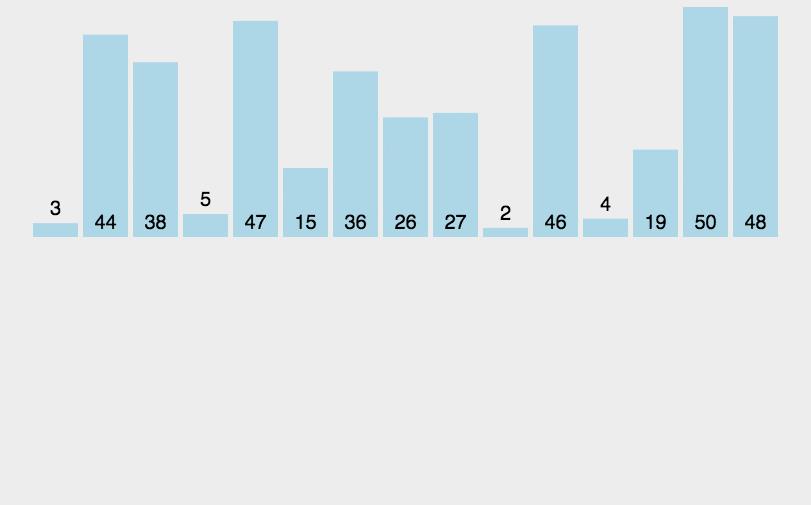
def insert_sort(li):
    for i in range(1, len(li)): # i是摸到的牌的下标
        tmp = li[i]     # tmp是摸到牌的值
        # 方法一
        j = i - 1 # j是手里最后一张牌的下标    li[j]是手里最后一张牌的值
        while j >= 0 and li[j] > tmp:   # 两个终止条件：j小于0表示tmp是最小的 顺序不要乱 
            li[j+1] = li[j]
            j -= 1
        # 方法二
        # for j in range(i-1, -1, -1):
        #     if li[j] > tmp:
        #         li[j+1] = li[j]
        #     else:
        #         break
        li[j+1] = tmp   #将摸到的牌 插入到 往前挪过之后的 j 的后一位

快速排序

def part(li, left, right):  # 列表,最左索引,最右索引
    tmp = li[left]  # 先找个临时变量把第一个元素存起来
    while left < right:  # 当最左小于最右
        while left < right and li[right] >= tmp:  # 当最左<最右 且 最右边的值大于等于临时变量
            right -= 1  # 最右 往左 挪 1 个单位长度
        li[left] = li[right]  # 都不满足:把挪完之后的最右的值 赋值给 最左的值(即最右的值小于临时变量时,这个值挪到当前最左的值)
        while left < right and li[left] <= tmp:  # 当最左<最右 且 最左边的值小于等于临时变量
            left += 1  # 最左 往右 挪 1 个单位长度
        li[right] = li[left]  # 都不满足:把挪完之后的最左的值 赋值给 最右的值(即最左的值大于临时变量时,这个值挪到当前最右的值)
    li[left] = tmp  # 当前最左最右的值相等时,把这个值赋给临时变量
    return left  # 返回当前临时变量的索引


def quick(li, left, right):
    if left < right:  # 如果左索引<右索引
        mid = part(li, left, right)  # 调用part进行分区 返回一个索引赋给mid
        quick(li, left, mid - 1)  # 递归调用quick 直到left=mid-1
        quick(li, mid + 1, right)  # 递归调用quick 直到mid+1=right


li = list(range(1000))
import random
random.shuffle(li)
print(li)

quick(li, 0, len(li) - 1)
print(li)

堆排序

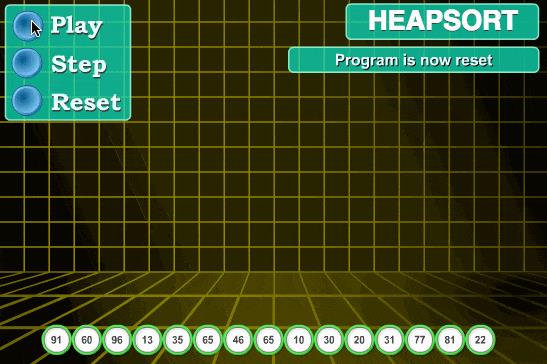
def sift(li, low, high):
    tmp = li[low]
    i = low
    j = 2 * i + 1
    while j <= high: # 退出条件2：当前i位置是叶子结点，j位置超过了high
        # j 指向更大的孩子
        if j + 1 <= high and li[j+1] > li[j]:
            j = j + 1 # 如果右孩子存在并且更大，j指向右孩子
        if tmp < li[j]:
            li[i] = li[j]
            i = j
            j = 2 * i + 1
        else:       # 退出条件1：tmp的值大于两个孩子的值
            break
    li[i] = tmp

@cal_time
def heap_sort(li):
    # 1. 建堆
    n = len(li)
    for i in range(n//2-1, -1, -1):
        # i 是建堆时要调整的子树的根的下标
        sift(li, i, n-1)
    # 2.挨个出数
    for i in range(n-1, -1, -1): #i表示当前的high值 也表示棋子的位置
        li[i], li[0] = li[0], li[i]
        # 现在堆的范围 0~i-1
        sift(li, 0, i-1)

归并排序

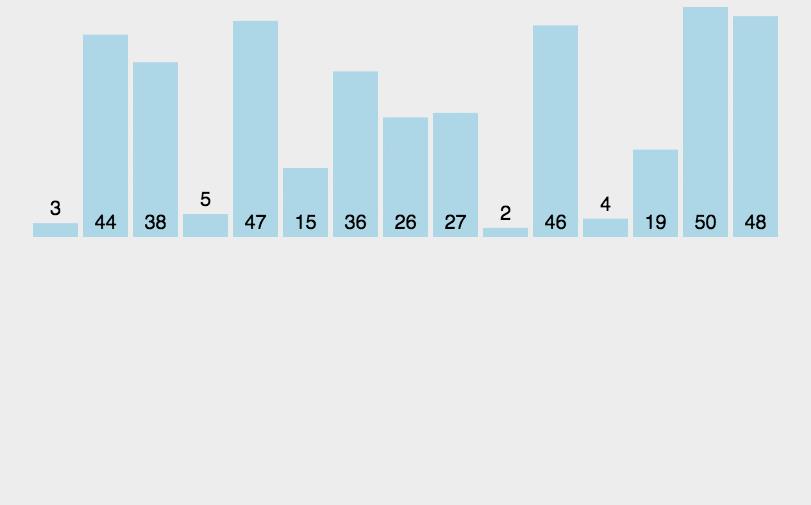
def merge(li, low, mid, high):
    i = low
    j = mid + 1
    ltmp = []
    while i <= mid and j <= high:
        if li[i] < li[j]:
            ltmp.append(li[i])
            i += 1
        else:
            ltmp.append(li[j])
            j += 1
    while i <= mid:
        ltmp.append(li[i])
        i += 1
    while j <= high:
        ltmp.append(li[j])
        j += 1
    # for k in range(low, high+1):
    #     li[k] = ltmp[k-low]
    li[low:high+1] = ltmp

def merge_sort(li, low, high):
    if low < high:
        mid = (low + high) // 2
        merge_sort(li, low, mid)
        merge_sort(li, mid+1, high)
        merge(li, low, mid, high)

# li = list(range(10000))
# random.shuffle(li)
# merge_sort(li, 0, len(li)-1)
# print(li)
li = [10,4,6,3,8,2,5,7]
merge_sort(li, 0, len(li)-1)

总结

---

识别图中二维码,欢迎关注python宝典