朝鲜红星操作系统加密算法解析

Posted 2021-04-19 嘶吼专业版

朝鲜的网络安全攻击能力非常强大，从众多的APT组织就可以看出。2015年，朝鲜号称自主研发了国产操作系统Red Star OS。Red Star OS具有监控模块和水印模块，可以自动为文档、图像甚至音频添加水印。据说水印功能是用来追踪媒体文件的。

在Red Star OS中，有三个kernel模块使有了专为Red Star OS定制的国产加密算法，这里分别将其命名为Jipsam1, Jipsam2, Pilsung。其中前两个在Red Star OS 2.0中，最后一个只出现在Red Star OS 3.0中。本文只对这些加密算法进行分析，这也是首篇对Red Star OS加密算法进行分析的文章。

AES Refresher

从下面的密码大体上基于AES结构的，所以先看一下AES的工作原理。下面是一个简单的应用过程，完整描述可以请参考FIPS-197。

这128比特的区块是按照4×4矩阵布局的，字节顺序如下图：

还有多轮加密过程，每轮都有下面的操作序列：

· SubBytes

· ShiftRows

· MixColumns

· AddRoundKey

SubBytes

SubBytes是AES中最复杂的操作，状态的每个字节都会被这一变换替换。

这里使用向量是对输入u进行倒数运算（0的倒数运算结果按0处理）。这一操作通常是通过查找表来应用的，但其结构的特点未来会变得特别重要。

ShiftRows

ShiftRows就是行变换的意思。第i行的元素会变i个位置，如下：

MixColumns

MixColumns更加复杂，含有一个很复杂的矩阵向量乘法运算，矩阵中的每一列都会乘以循环矩阵。

需要注意的是上面矩阵中的元素并不都是整数，这些元素是SubBytes中用于多项式乘法的相同区域的standin。2对应的是乘x模，3对应的是乘x+1模。

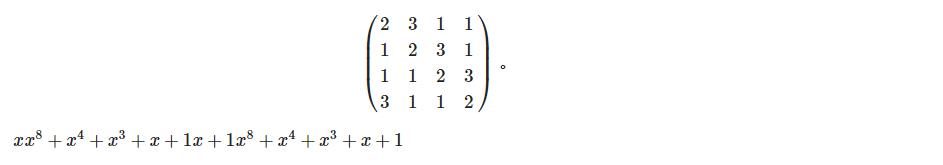
AddRoundKey

AddRoundKey就是分别对round key进行异或运算然后插入state（状态）中。

# Jipsam1

Jipsam1与AES-256类似，kernel模块中是使用的代码是从Rijndael应用中直接复制过来的。因此，这是一个256位密钥的128位区块加密方法。

Jipsam1和AES-256的区别就在于S-box。在AES中，S-box是公开的并且是常量：

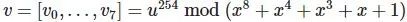
这里的向量是对输入字节u的倒数运算。

而在Jipsam1中，affine transformation（仿射变换）的常量组件在第r轮从0x63 = [1,1,0,0,0,1,1,0]变为

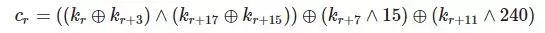
也就是说每一轮都有一个定制的S-box，这会影响每个round key的key安排。

与AES相比，这种方式并不会增强安全性。因为只有AES的affine组件受影响，密码的非线性和差分特性是不变的。这对integral attack（积分攻击）的防御有所改善，但并没有改善太多。另一方面，该方案是基于key的，也很难分析。研究发现，与固定公开的S-box相比，加入密码S-box的AES其实并没有优势。

下面是对AES进行简单修订的Jipsam1的应用：

--- a/rijndael.cpp

+++ b/jipsam1.cpp

 

-static uint8_t SubByte(const uint8_t x0) {

+static uint8_t SubByte(const jipsam1_ctx * ctx, size_t r, const uint8_t x0) {

+  const uint8_t   k = ((ctx->k[r+0] ^ ctx->k[r+3]) & (ctx->k[r+17] ^ ctx->k[r+15])) ^

+                 (ctx->k[r+7] & 0x0F) ^ (ctx->k[r+11] & 0xF0);

   const uint8_t  x1 = multiply( x0,  x0); // x^2

   const uint8_t  x2 = multiply( x1,  x0); // x^3

   const uint8_t  x3 = multiply( x2,  x2); // x^6

@@ -49,7 +51,7 @@ static inline uint8_t SubByte(const uint8_t x0) {

   const uint8_t x10 = multiply( x9,  x0); // x^127

   const uint8_t x11 = multiply(x10, x10); // x^254 = x^-1

   return x11 ^ rotate_left(x11, 1) ^ rotate_left(x11, 2) ^

-         rotate_left(x11, 3) ^ rotate_left(x11, 4) ^ 0x63;

+         rotate_left(x11, 3) ^ rotate_left(x11, 4) ^ k;

 }

Jipsam2

Jipsam2是Red Star OS使用的第二个加密算法。设计者的设计思路是另一个方向——构图和状态。该组件使用的是AES-256和RC4。下面是一个应用：

256位key被分成2个128位，被用来初始化2个RC4状态S0和S1，之后32字节的keystream都会被丢弃。

为了加密新的128位区块，每个状态Si会从流S0和S1生成32字节。然后加密继续进行：

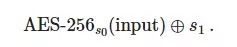
换句话说，Jipsam2是将RC4和AES结合在一起的操作状态模式，每个区块都使用新的256位AES密钥。因为使用了RC4，看起来好像安全一点。但实际上RC4没有什么用，因为所有的事情都可以用AES完成。

Pilsung

Pilsung是Red Star OS 3.0使用的最新、最复杂的算法。与Jipsam1类似，Pilsung是128位的块加密算法。但Pilsung对加密过程做出了更大的变化。Pilsung使用了含有真随机的S-box的AES算法，理论上对大量攻击都是安全的。

Pilsung除了有随机的S-box外，还可以对AES的ShiftRow步骤随机化，生成一个16字节状态的随机序列。目前还不清楚这一步骤的具体目的，但这与SASAS方案比较像，在SASAS方案中，所有的替代和线性层都是秘密的。

加密过程基本上与AES相同，10轮到替代序列网络，包括SubBytes，ShiftRows，MixColumns和AddRoundKey。下面分析Pilsung各功能：

SubBytes

Pilsung的SubBytes与AES系统。在AES S-box应用之后，产生的字节会通过一个随机的位序列，这与状态字节是不同的，随后与常数3进行XOR运算。

ShiftRows

Pilsung的ShiftRows并不改变行，而是对状态的16字节应用随机序列。

MixColumns

MixColumns与AES完全相同。

AddRoundKey

AddRoundKey与AES完全相同。

Key Derivation

SubBytes和ShiftRows会使用大量的随机序列。在SubBytes中，是状态的8位序列，在ShiftRows中是状态的16字节序列。而这些序列是从key中提取出来的。

Pilsung加密本身是非常直接的，而其关键计划还是非常精细复杂的。首先，256位的key会传递给基于SHA-1的key derivation函数，可以从key中提取32字节的key。然后，key会检查AES key 方案，但只使用了key material中的160位。这也并不是一个bug，而是扩展key的11×16=176字节。

SHA-1应用的key derivation稍微有点变化：输出的4i+3字节是按位求反对。

Generating Permutations

Pilsung会使用相对模糊的方法来生成序列。其开发者使用了Rao-Sandelius shuffle的变种，这与基数排序（radix sort）类似。这个想法也非常简单：

· 把数组分成两部分，按掷硬币的方法随机选择一组；

· 递归地将选择地分组进行分割，直到一组只有一个单独的元素。

这是一种经常使用的技术，其缺点是组之间是不平衡的。其中一个组中含有的元素可能会多于另一组。如果需要保持平衡，就需要进行nlogn+O(n)次投掷，而不是nlogn。

8个元素的每个序列都会使用AES key方案的1字节，然后将其随机地扩展成24位。

// Distribution sort: sort array p of size n according to 0-1 array s

// Assumes s has n / 2 zeros and n / 2 ones

void Get_One(const uint8_t * s, uint8_t * p, size_t n, uint8_t * buf) {

  size_t a = 0, b = 0;

  for(size_t i = 0; i < n; ++i) {

    if( s[i] )

      buf[n / 2 + a++] = p[i];

    else

      buf[b++] = p[i];

  }

  memcpy(p, buf, n);

}

 

// Generate a random permutation of [0..7]

void Get_P8forSEnc(uint8_t perm[8], uint8_t random_bits) {

  uint8_t coinflips[24];

 

  // Random 4-bit subset

  uint8_t v0 = Tree_Integer8[random_bits % 70];

  for(size_t i = 0; i < 8; ++i) {

    coinflips[i] = (v0 >> (7 - i)) & 1;

  }

 

  uint8_t v1 = (Tree_Integer4[(random_bits & 0x0F) % 6] << 0) |

               (Tree_Integer4[(random_bits >> 4) % 6] << 4);

  for(size_t i = 0; i < 8; ++i) {

    coinflips[i+8] = (v1 >> (7 - i)) & 1;

  }

 

  for(size_t i = 0; i < 8; i += 2) {

    if( random_bits & (3 << i) ) {

      coinflips[16+i+0] = 1;

      coinflips[16+i+1] = 0;

    } else {

      coinflips[16+i+0] = 0;

      coinflips[16+i+1] = 1;

    }

  }

 

  // Initialize permutation with identity

  for(size_t i = 0; i < 8; ++i)

    perm[i] = i;

 

  // Iterative version of the Rao-Sandelius shuffle

  uint8_t scratch[32];

  for(size_t i = 0; i < 3; ++i) {

    const size_t bins = 1 << i;       // number of subgroups

    const size_t size = 1 << (3 - i); // size of each subgroup

    for(size_t j = 0; j < bins; ++j) {

      Get_One(&coinflips[i * 8 + j * size], &perm[j * size], size, scratch);

    }

  }

}

Tree_Integer{4,8}是一个分别结合了4比特和8比特的平衡单词表。前者共有C(4,2)=6种，后者共有C(8,4)=70种。其实if( random_bits & (3 << i) )并不是公平的，从这里获取的序列也不是真随机的。

16字节的序列使用的是同样的方法，但使用的是AES key方案的16字节来生成64次掷硬币模拟。

// Generate a random permutation of [0..15] at output

void Get_P16Enc(uint8_t output[16], const uint8_t input[16]) {

  uint8_t coinflips[64];

 

  // coin flips for first level

  for(size_t i = 0; i < 4; ++i) {

    uint8_t v0 = Tree_Integer4[(input[i] ^ input[i+4]) % 6];

    for(size_t j = 0; j < 4; ++j) {

      coinflips[4*i+j] = (v0 >> (7 - j)) & 1;

    }

  }

 

  // coin flips for second level

  for(size_t i = 0; i < 8; ++i) {

    if((input[i] >> i) & 1) {

      coinflips[16 + 2*i + 0] = 1;

      coinflips[16 + 2*i + 1] = 0;

    } else {

      coinflips[16 + 2*i + 0] = 0;

      coinflips[16 + 2*i + 1] = 1;

    }

  }

 

  // coin flips for third level

  for(size_t i = 0; i < 4; ++i) {

    uint8_t v1 = Tree_Integer4[(input[i+8] ^ input[i+12]) % 6];

    for(size_t j = 0; j < 4; ++j) {

      coinflips[32+4*i+j] = (v1 >> (7 - j)) & 1;

    }

  }

 

  // coin flips for fourth level

  for(size_t i = 0; i < 8; ++i) {

    if((input[8+i] >> i) & 1) {

      coinflips[48 + 2*i + 0] = 1;

      coinflips[48 + 2*i + 1] = 0;

    } else {

      coinflips[48 + 2*i + 0] = 0;

      coinflips[48 + 2*i + 1] = 1;

    }

  }

 

  // Initialize permutation with identity

  for(size_t i = 0; i < 16; ++i)

    output[i] = i;

 

  // Iterative version of the Rao-Sandelius shuffle

  uint8_t scratch[32];

  for(size_t i = 0; i < 4; ++i) {

    const size_t bins = 1 << i;       // number of subgroups

    const size_t size = 1 << (4 - i); // size of each subgroup

    for(size_t j = 0; j < bins; ++j) {

      Get_One(&coinflips[i * 16 + j * size], &output[j * size], size, scratch);

    }

  }

}

如果直接使用key material的128位来作为掷硬币的结果更简单。

安全性

这个构造看起来非常安全，但这都是在AES的基础上完成的。但是：

· 序列并不是完全随机的；

· 这种随机性并不是独立的，S-box和序列都来自同样的key位；

· S-box并不是真随机的，Baignères-Vaudenay的安全结果并未应用到这里；

· ShiftRows操作的随机并不是必要的；

总的来说，设计者有比Baignères & Finiasz的使用A+B/x形式的S-BOX更好的方法。 

总结

朝鲜在网络安全领域已经成为第一梯队。智库分析称Sony被黑、WannaCry、和最近的TYPEFRAME、HIDDEN COBRA等活动背后都是朝鲜网军在运作。在加密方面，从收集的情报分析看，主要使用AES的简单变种，但也是一个不错的选择。

总的来说，加密都是基于西方的区块加密，比如AES，RC4，SHA-1等；除了对内部组件进行随机化外都没有大的改进，其中的原因有：

· 朝鲜并没有泄露这方面的能力；

· 缺乏关于内部加密的研究。

虽然这种加密算法可能会受到侧信道攻击，但韩国的ARIR、中国的SM4、日本的Camellia、俄罗斯的Kuznyechik等都借鉴了AES。