动态规划-矩阵连乘问题

Posted 2021-04-18 咸鱼成长小站

问题描述

给定n个矩阵{A1，A2,…,An}，其中Ai与Ai+1是可乘的，i = 1,2,…,n-1。如何确定计算矩阵连乘积的计算次序，使得依次次序计算矩阵连乘积需要的数乘次数最少。

这题的意思呢，就是有n个矩阵连乘，我们知道矩阵的乘法不满足交换律，但是满足结合律。也就是说n个矩阵相乘的时候。我们可以选择不同的计算次序，也就是决定哪两个先乘。不同的计算次序我们所需要进行的数乘次数是不同的。

那么矩阵相乘的数乘次数怎么算。我们列举两个矩阵A和B：

A和B能够相乘，因为A的列数等于B的行数。我们计算A乘B，就是将A的每一行分别乘上B的每一列。对于这个A为2行3列，B为3行2列的矩阵来说。数乘次数就是2x3x2。
也就是

第一个矩阵的行数 x 第一个矩阵的列数（第二个矩阵的行数） x 第二个矩阵的列数

3个以上的矩阵相乘时，由于我们选择的计算次序不同，我们所需要进行的数乘次数也会不一样。
例如：
4个矩阵ABCD，设它们维数分别为
A:50x10 B:10x40 C:40x30 D:30x5
则它的计算次序以及数乘次数有以下几种：

加括号方式	连乘积计算量
(A(B(CD)))	40x30x5+10x40x5+50x10x5 = 10500
(A((BC)D))	10x40x30+10x30x5+50x10x5 = 16000
((AB)(CD))	50x10x40+40x30x5+50x40x5 = 36000
(((AB)C)D)	50x10x40+50x40x30+50x30x5 = 87500
((A(BC))D)	10x40x30+50x10x30+50x30x5 = 34500

求解这个问题，我们可以这么想，无论多少个矩阵连乘，无论选择怎样的次序，我们每次计算的都是两个矩阵的连乘积。比如ABCD，我们选择次序为(A(B(CD))),第一次我们计算的是CD，CD乘完后得出一个临时矩阵T，第二次我们计算的就是B和T。得到临时矩阵T2，接着计算的就是A乘T2。
那么，我们可以用分治法的思想，n个矩阵连乘。我们看作A[1:n]。我们就可以分为两段[1:k]和[k+1:n]（ k = 1,2,…,n-1）。也就是计算次序我们从中间断开，加括号于k和k+1之间。即(A1…Ak)(Ak+1…An)。然后我们在分别递归计算A[1:k]和A[k+1:n]的计算次序。然后这两个结果相乘就得到了A[1:n]。
所以对于矩阵连乘序列A[i:j]来说，它的数乘次数M[i:j]就有一个递归公式如下：

其中P(i-1)代表矩阵Ai的行数，Pk代表Ak的列数。Pj代表Aj的列数。
通过实现这个递归公式，我们就可以做到用分治法来求解这一题。但是！这么做我们的效率是不高的。我们来看一下递归求解M[1:4]将经历哪些步骤

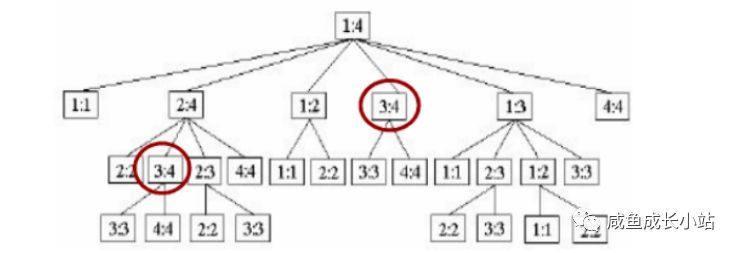
从上图我们可以看到，在我们递归求解的过程中，进行了非常多的重复运算，这就是为什么说分治法解决这一题是一个可行的方法，但不是一个有效的算法。
那么，我们怎样去避免这些重复的运算呢？
很简单，既然你计算一个问题的过程中可能会去计算很多重复的子问题。那么我就先去计算那些子问题，并将子问题的解先保存下来。那么在我需要再次去计算子问题的时候，只需要去查一下表就行了。
也就是将一个自顶向下的计算过程改为自底向上的计算，先解决规模最小的子问题。然后逐层往上解决，在你需要子问题的解时，我只需要去查一下保存的值即可。这样就不用进行重复的计算。
接下来我们来解一个具体的例题：
4个矩阵ABCD连乘，设它们维数分别为
A:50x10 B:10x40 C:40x30 D:30x5
求怎样的计算次序使得数乘次数最少？

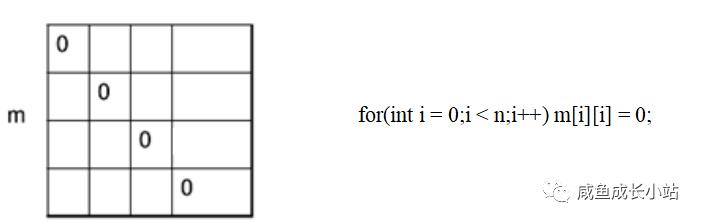
接下来，我们求次一级规模，次一级就是两个矩阵连乘。即A[1:2],A[2:3],A[3:4]三种。
根据我们之前的递归公式可以知道:(注：由于我们m矩阵的行与列均是从0开始，所以代码写出来与递归公式有所差异)

m[0][1] = m[0][0] + m[1][1] + p[0]*p[1]*p[2];
m[1][2] = m[1][1] + m[2][2] + p[1]*p[2]*p[3];
m[2][3] = m[2][2] + m[3][3] + p[2]*p[3]*p[4];

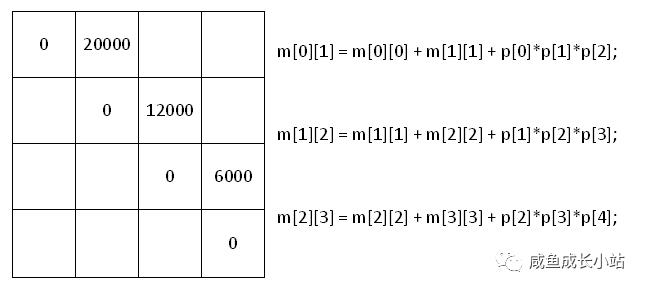
然后我们再往上求，这次就得求三个矩阵连乘的情况，即A[1:3],A[2:3]两种情况。根据递归公式可得：

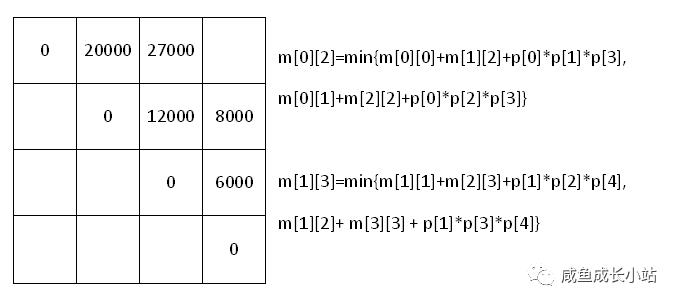
在我们需要使用子问题的解如m[1][2]时，只用查表就行了。
最后就是计算我们题目要求的，4个矩阵连乘时的最少数乘次数。

这样，m[0][3]就是A[1:4]的最少数乘次数。
可以看到我们的计算次序是这样的：

我们还可以添加一个二维数组s。在每一次计算的时候呢，将最少数乘次数所选择断开的点也就是k+1给记录下来。

通过这个矩阵，我们就能够将取得最少数乘次数的计算次序还原回来
如A[1:4]，我们查表s[0][3]得1，我们就知道断在第一个矩阵，所以就分为了A[1:1]和A[2:4]。序列变为(A(BCD))。
我们继续查表s[1][2]得2，则第二次断在第二个矩阵，分为A[2][2]和A[3][4]。序列变为(A(B(CD)))
这就是我们得到的最优计算次序。

下面是完整的代码：

 1#include <iostream>
 2#include <string>
 3void matrix(int **M, int* P, int n, int **S) {                        //计算数乘次数以及加括号位置
 4    for (int r = 1; r < n; r++){
 5        for (int i = 0; i < n-r; i++){
 6            int j = i + r;
 7            M[i][j] = M[i + 1][j] + P[i] * P[i + 1] * P[j + 1];                     //先对m[i][j]一个初始值
 8            S[i][j] = i + 1;
 9            for (int k = i + 1; k < j; k++){                                        //循环寻找数乘次数最少的情况
10                int t = M[i][k] + M[k + 1][j] + P[i] * P[k + 1] * P[j + 1];
11                if (t < M[i][j]){
12                    M[i][j] = t;
13                    S[i][j] = k + 1;
14                }
15            }
16        }
17    }
18}
19void show(int **S,std::string* matrixlist,int i,int j) { //输出函数
20    if (i == j)                                                     
21        std::cout << matrixlist[i];
22    else {
23        int k = S[i][j];
24        std::cout << '(';                               //先输出左括号
25        show(S, matrixlist, i, k-1);                    //递归调用输出左边部分的加括号方式
26        show(S, matrixlist, k, j);                      //递归调用输出右边部分的加括号方式
27        std::cout << ')';                               //输出右括号
28    }
29}
30void main() {
31    int n;
32    std::cout << "请输入矩阵个数n：";
33    std::cin >> n;
34    int **M = new int*[n];
35    int **S = new int*[n];
36    int *P = new int[n + 1];
37    std::string *matrixlist = new std::string[n];
38    for (int i = 0; i < n; i++) {
39        M[i] = new int[n];
40        S[i] = new int[n];
41    }
42    for (int i = 0; i < n; i++) {
43        for (int j = 0; j < n; j++){                        //初始化M矩阵
44            M[i][j] = 0;
45            S[i][j] = 0;
46        }
47    }
48    std::cout << "请输入各个矩阵的编号：";
49    for (int i = 0; i < n; i++){
50        std::cin >> matrixlist[i];
51    }
52    std::cout << "请输入各个矩阵的维度信息(n+1个整数)：";
53    for (int i = 0; i <= n; i++){
54        std::cin >> P[i];
55    }
56    matrix(M, P, n, S);                                 //计算M矩阵与S矩阵
57    std::cout << "M矩阵" << "
	";
58    for (int i = 1; i <= n; i++){
59        std::cout << i << "	";
60    }
61    std::cout << std::endl;
62    for (int i = 0; i < n; i++)     {
63        std::cout << i + 1 << "	";
64        for (int j = 0; j < n; j++){
65            std::cout << M[i][j] << "	";
66        }
67        std::cout << std::endl;
68    }
69    std::cout << "S矩阵" << "
	";
70    for (int i = 1; i <= n; i++){
71        std::cout << i << "	";
72    }
73    std::cout << std::endl;
74    for (int i = 0; i < n; i++){
75        std::cout << i + 1 << "	";
76        for (int j = 0; j < n; j++){
77            std::cout << S[i][j] << "	";
78        }
79        std::cout << std::endl;
80    }
81    std::cout << "矩阵连乘最少数乘加括号方式为：";
82    show(S, matrixlist, 0, n-1);                            //输出加括号方式
83    std::cout << std::endl;
84    system("pause");
85}

最终结果示意图：