见闻广博|动态规划小入门
Posted ECNU极客空间
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了见闻广博|动态规划小入门相关的知识,希望对你有一定的参考价值。
-Dynamic-
Programming
相信大家考过第一次程序能力实训的同学们一定对一个难度颇大的题目记忆犹新吧 ↓


毫无疑问,这道题之所以难倒了大多数上午考的同学。问题在于大家对dp,即动态规划的不了解(据说暴力求解能拿70)我们遇到的问题中,有很大一部分可以用动态规划(简称DP)来解。解决这类问题可以很大地提升解题能力与技巧。
动态规划(Dynamic Programming,简称DP),简单来说就是通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划算法通常基于一个递推公式及一个或多个初始状态。当前子问题的解将由上一次子问题的解推出。使用动态规划来解题只需要多项式时间复杂度,因此它比回溯法、暴力法等要快许多。
今天,小编在此想给大家归类总结一些简单的dp算法。(听说往下看的同学实训都会过哦!)
动态规划


一个简单的问题:
从一个棋盘的左上角走到右下角最少要用多少步?
你每步只能走一格,因为东南西北随便走,所以如果你随便走四步可能会处于很多不同的位置,我们把这每个可能的位置称为状态,所有可能的位置的集合叫做阶段。
现在问题来了!有了这些概念之后,计算新状态可能遇到各种奇葩的情况。
对于不同的情况我们有不同的算法:
假如问题有n个阶段,每个阶段都有不同的状态,一个阶段的一个状态可以得到下一个阶段的所有状态中的几个,那我们想得到最终的状态自然要经历之前每个阶段的某些状态。

好消息是我们有时候并不需要计算所有的状态,我们再回到最初的例子,答案很显然,某个阶段确实有可能有很多状态,正如这个问题中走n步可以走到很多位置一样。但是在同样走n步的所有位置中,哪些位置可以让我们在走第n+1步时走的最远呢?没错,正是第n步中最远的位置。换句熟悉的话来说“下一步最优是由当前最优得到的”,为了计算最终的最优值,只要储存每一步的额最优值即可。这是所谓的贪心算法,计算的方法是递推。

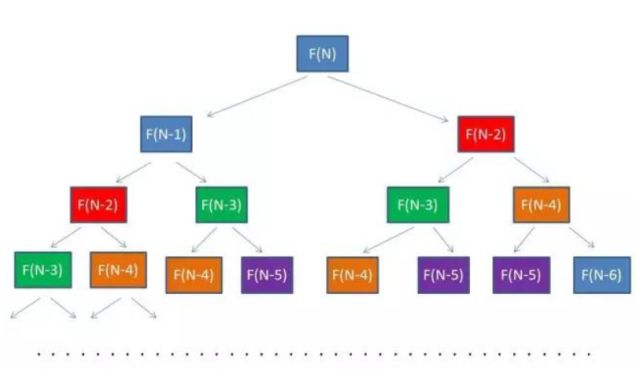
OK,讲了这么多具体的东西,让我们来点抽象的。从以上的文字中,我们要抽出动态规划里非常重要的一个概念:状态转移方程。
著名程序设计书籍算法导论中提到动态规划算法通常经历四个步骤:
1、刻画一个最优解的结构特征。
2、递归地定义最优解的值。
3、计算最优解的值,通常采用自底向上的方法。
4、利用计算出的信息构造一个最优解。
对于确定状态转移方程就在第一步和第二步中,首先要确定问题的决策对象,接着对决策对象划分阶段并确定各个阶段的状态变量,最后建立各阶段的状态变量的转移方程。
比如找一列数当中最大的那个数,如果你知道了前n个数中最大的,记为MAX_n,当你遇到第n+1个数时,就是拿着个数跟之前的MAX_n比较,然后留下大的那个,写下来就是:
MAX_n+1=(X_n+1>MAX_n)?X_n+1:MAX_n
这就是一个简单的状态转移方程。
动态规划方程包含了三个条件,一状态转移方程,二最优值函数,三边界条件。状态转移方程就是动态过程的“动力”,我们在知道了k阶段的状态和决策后就可以得到k+1阶段的状态(反之同理),它把各个阶段联系起来了,因而我们才可以从边界条件通过递推得到最优解。


好了,本期内容暂时小编给大家整理到这里,有什么意见可以在留言板上提出哦!
(往下拉有惊喜)

向左滑动查看~
小编
是的没错,彩蛋来了!
小编为大家整理了一些经典dp问题的博客:
1. 背包问题
woj 1537 A Stone-I 转化成背包
woj 1538 B Stone-II 转化成背包
poj 1170 Shopping Offers 状压+背包
zoj 3769 Diablo III 带限制条件的背包
zoj 3638 Fruit Ninja 背包的转化组合数学
hdu 3092 Least common multiple 转化完全背包
poj 1015 Jury Compromise 扩大区间+输出路径
poj 1112 Team Them UP 图论+背包
66分钟前


小明,王老师,李大哥,五舍宿管陈阿姨
王大哥:大哥,稳!
2. LIS(最长递增子序列)
uva 10635 Prince and Princess LCS转化成LIS
hdu 4352 XHXJ's LIS 数位dp+LIS思想
srm div2 1000 状态压缩+LIS
poj 1239 Increasing Sequence 两次dp
3. 区间dp
poj 1141 Brackets Sequence 括号匹配
hdu 4745 Two Rabbits 转化成求回文串
zoj 3541 The Last Puzzle 贪心+区间dp
poj 2955 Brackets
以上部分内容来自知乎
https://blog.csdn.net/cc_again/article/details/25866971
66分钟前
鲍老师,王老师,小孔,秋林阁吴师傅
排版:刘叶婷
文案:廖涌祥
以上是关于见闻广博|动态规划小入门的主要内容,如果未能解决你的问题,请参考以下文章