强化学习-动态规划精简版

Posted 2021-04-18 CCH陈常鸿

强化学习导论依然坚持在翻译，但工作量实在太大，先给出精简版。

动态规划（Dymamic Programming）以下简称DP。

DP要求一个完全已知的环境模型，MDP五元素全部知道。

你不记得什么是MDP五元素？MDP五元素为S,A,P,R,gama，分别对应状态(state)，动作（action），状态转移概率（比如你到一个十字路口，你目前的状态(s)就是站在路口准备向下一个方向走，你有前后左右四个选择，假如你往左走的概率是20%，那么你从站立状态到往左走状态的状态转移概率为20%），奖励（reward），惩罚因子（gama）

DP是有模型学习（model-base learning）

强化学习是序列决策问题（就像过十字路口，要先走到路口才有下一步），DP也是序列决策问题，不同的是DP是环境已知，agent不需要靠与环境的交互来获取下一个状态（在十字路口中，到路口自然选择方向，没有与环境交互，比如红绿灯这些），而是知道自己执行某个动作后面的状态是什么，然后优化自己的策略。

动态规划是将一个复杂的问题一系列简单的问题，一旦解决这些简单的问题，再将子问题结合起来，解决复杂的问题，并且同时将它们的解保存起来。

D是指状态是step-by-step的（序列化问题，路口时一个一个走的）

P是指优化成子问题，通过贝曼方程MDP被递归的切成子问题，同时它有值函数，保存了每个子问题的解，因此它能通过动态规划来求解。针对MDP，切成的子问题就是在每个状态应该选择的action，MDP的子问题是一种递归的方式存在，在一时刻的子问题，取决于上一个问题选了哪个action（十字路口选了一个方向，那么下一个路口选择就与前一个路口的其他选择无关了）。

DP分两部分：一是预测（prediction），也就是已知MDP的状态，动作，奖励，状态转移率，惩罚因子和策略，求出每一个状态的值函数，也就是每一个状态下能获得reward是多少。二是控制，S,A都已知，在策略(policy）未知的情况下，计出最优的值函数，并且借此计算最优策略。

DP->policy iteration->policy评估->policy iteration ->policy评估...

Policy Iteration:

1）Policy evalution：基于当前的policy计算出每个状态的值函数。

2）Policy improvement：基于当前值函数，利用贪心算法找到当前最优的Policy。

对于一次迭代，状态S的价值等于前一次迭代该状态的额即时奖励与所有S的下一个可能状态，S`的价值与其概率成绩之和。

矩阵形式：

例子：

状态空间：S1-S14为非终止状态，S0和S15为终止状态。

动作空间：A{上，下，左，右}，只有非终止状态下才有动作。

R：S1-S14为-1，S0和S15为1.

惩罚系数gama为：1

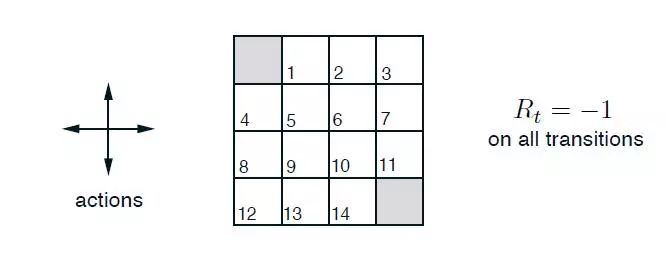
边界的数字若往外则以自身状态作为状态。

问题：评估在这个世界里给定的策略

策略迭代(Policy Iteration)：

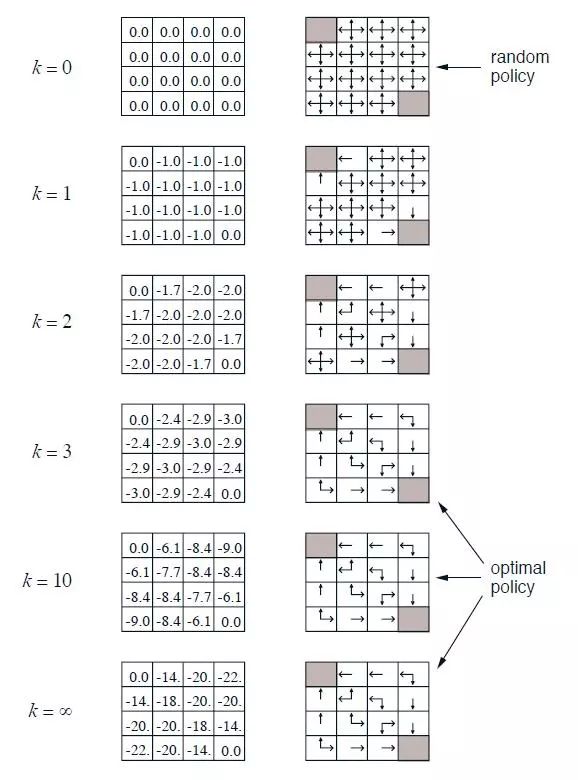
这是强化学习给出的过程图，但具体整么算不是很清楚，我自己写了具体计算过程（从右往左看）

在迭代次数足够多的情况下，可以得到一个近似的全部状态的值函数表。

上面是一个基本的策略评估过程，没有进行策略改进。

如果长时间的迭代后，策略收敛并不明显，先状态值函数估计一段时间，然后看策略如何，根据各个状态的值函数，给出一个相对比初始随机要好一点的策略，然后根据这个策略再次进行值函数评估，反复如此，这就是策略迭代。

策略迭代就是当前策略迭代出V值，再根据V值贪婪地更新策略，反复，最终得到最优策略π*和最优策略状态价值函数V*.

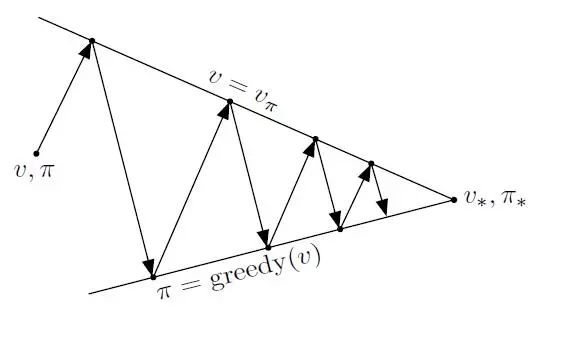
一般策略更新收敛速度会比状态价值函数值得收敛快很多。

价值迭代（Value Iteration）

优化原则：一个最优策略可以被分解为两部分，一部分从状态S到下一个S`采取了最优行为A*，另一部分就是在状态S`时遵循一个最优策略。

定理：一个策略能够使得状态S获得最优值，当且仅当，对于从状态S可以到达任何状态S`，该策略能够使状态S`的价值是最优价值。

确定性价值迭代，在前一个定理的基础上，如果知道goal的状态的位置以及反推需要明确的状态间关系，这就是一个确定性的价值迭代。

此时，我们可以把问题分解成一系列的的子问题，最终目标开始分析，逐渐往回推。

价值迭代，从初始状态价值开始迭代计算，最终收敛，整个过程没有遵循任何策略。与策略迭代不同，在价值迭代过程中，算法不会给出明确的策略，迭代过程得到价值函数不会对应任何策略。价值迭代虽然不需要策略参与，也要知道，状态间的转换率，也就是知道模型。

动态规划的两个问题：预测和控制。预测问题就是给定策略去计算各状态的价值函数。

控制问题就是通过策略迭代，先给定或随机策略下计算状态价值函数，根据状态函数贪婪更新策略。单纯的价值迭代也可以，但要知道S在a后到达所有后续状态及概率。