搜索与动态规划 | 搜索的知识点归纳

Posted 2021-04-18 星蓝翰元教育

搜索与动态规划-搜索的知识点归纳

01

概论

 搜索算法是利用计算机的高性能来有目的的穷举一个问题解空间的部分或所有的可能情况，从而求出问题的解的一种方法。在竞赛中，搜索法还被当做“救命稻草”——大多数问题都可以使用搜索来谋取部分分数。

搜索策略有很多，常见的有：深度优先搜索、宽度优先搜索、迭代加深搜索等。搜索算法的设计主要是一下几个步骤：确定状态和扩展方式、选用合适的搜索方式、优化。

02

知识点归纳

深度优先搜索与宽度优先搜索

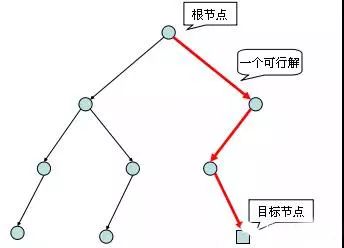
搜索算法设计过程中，主要需要考虑的问题有两个：状态与状态之间的关系（即扩展方式）。如果将状态对应顶点，状态之间的关系对应边，原搜索问题可抽象成一棵搜索树。初始状态对应根节点，目标状态对应目标节点，搜索算法即找到一条从根节点到目标节点的路径（一个可行解）。详见下图：

不同的搜索算法相当于搜索树的不同遍历方式。最常见的深度优先搜索（DFS -- Depth First Search）和宽度优先搜索（BFS -- Breadth First Search）对应着搜索树的两种遍历方式，如下图：

深度优先搜索所遵循的搜索策略是尽可能“深”地遍历搜索树，对应树的前序遍历。在深度优先搜索中，对于当前节点，如果有可行子节点，则向下遍历，否则回溯。

宽度优先搜索所遵循的搜索策略是尽可能“广”的遍历搜索树，对应树的分层遍历。在宽度优先搜索中，每次都先将搜索树某一层的所有结点全部访问完毕后再访问下一层，首次达到的目标节点通常就是最优解。

深度优先搜索与宽度优先搜索有不同的应用，大致如下表：

项目/特性

优势

劣势

深度优先搜索（DFS）

1. 比较适合回溯类搜索

2. 参数传递、状态修改和恢复都比较方便

3. 自顶向下地处理问题

4. 能很快到达解答树的底端

1. 使用递归算法容易导致栈溢出

2. 可能产生冗余搜索

宽度优先搜索（BFS）

1. 容易解决“最少步数”、“深度最小”问题

2. 问题的解靠近解答树的根结点

3. 启发式搜索在BFS中更容易实现

1. 空间一般比DFS大

2. 状态重复的排除有时耗时多

 迭代加深搜索

迭代加深搜索是权衡深度优先搜索和宽度优先搜索的利弊后的搜索策略。迭代加深搜索实质是限定下界的深度优先搜索，即首先允许深度优先搜索搜索k层搜索树，若没有发现可行解，则增加搜索树深度至k+1，再次执行深度优先搜索。迭代加深搜索算法比起宽度优先搜索牺牲了时间，但节约了空间。迭代加深搜索的时间不会超过等效BFS占用时间的两倍，当数据规模增大时，二者的差距还会逐渐减小，而迭代加深搜索的空间占用和DFS一样小。另外迭代加深搜索跟DFS一样，在某些问题上需要判断重复。

搜索算法的优化

没有任何优化的搜索算法又被称为“裸搜”，其时间复杂度通常很高，通常由以下两方面的影响：搜索时产生了无用节点、重复搜索。搜索算法的优化主要也基于这两方面进行。

解决重复搜索问题，不论深度优先搜索还是宽度优先搜索，都使用状态记录来解决。在搜索的过程中，记录搜索状态，当搜索到与之前的状态相同的状态时，即可舍去该子树。记录状态通常由两种方式，一种是将状态按照一定的策略进行排序；另一种则是用散列（Hash）表。

解决搜索时产生了无用节点问题，大致有两种策略，一种是剪枝，另一种是改进搜索顺序。

剪枝主要应用于深度优先搜索，其主要方式有两种，一种是可行性剪枝，另一种是最优化剪枝。当搜索到某一节点后，可行性剪枝即继续搜索不能够产生一个可行解时，可立即回溯；最优化剪枝即继续搜索不能够产生比当前最优值更优的解时，可立即回溯。

改进搜索顺序方式主要有两种，一种是随机化搜索，另一种是启发式搜索。随机化搜索主要应用与深度优先搜索，其策略为随机选取节点的子节点进行扩展。随机化搜索的好处是可以避免原问题的顺序性带来的影响。启发式搜索跟宽度优先搜索类似，不同的是，宽度优先搜索仅仅用和根节点的距离作为权重，而启发式搜索则是设计一个估价函数，每次扩展按照该估价函数最大的节点进行扩展。这些优化策略会在例题解析中详细讲述。