学小实，学大事 | 动态规划算法

Posted 2021-04-18 信彩飞扬

在上一期对论文写作格式的介绍后，小伙伴们有没有对“挑战杯”论文大赛感兴趣呢？这一期，我们将继续介绍经典的算法。大名鼎鼎的五大经典算法包括分治法、动态规划、贪心法、回溯法以及分支限界法。在前面的几期学小实里，我们介绍了分治算法。这一期我们将对同属于五大经典算法之一的动态规划算法进行介绍。

一、基本概念

动态规划(dynamic programming)是运筹学的一个分支，是求解决策过程(decision process)最优化的数学方法。20世纪50年代初美国数学家R.E.Bellman等人在研究多阶段决策过程(multistep decision process)的优化问题时，提出了著名的最优化原理(principle of optimality)，把多阶段过程转化为一系列单阶段问题，利用各阶段之间的关系，逐个求解，创立了解决这类过程优化问题的新方法——动态规划。动态规划的经典题目包括最长回文字串、最大子数组和、切割回文数、最长公共子序列、最长子串、最长递增子序列、背包问题等。

动态规划常常适用于有重叠子问题和最优子结构性质的问题，动态规划方法所耗时间往往远少于朴素解法。

 二、基本思想与策略

动态规划背后的基本思想非常简单。大致上，若要解一个给定问题，我们需要解其不同部分（即子问题），再根据子问题的解以得出原问题的解。通常许多子问题非常相似，为此动态规划法试图仅仅解决每个子问题一次，从而减少计算量：一旦某个给定子问题的解已经算出，则将其记忆化存储，以便下次需要同一个子问题解之时直接查表。这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。

动态规划法与分治法最大的差别是：适合于用动态规划法求解的问题，经分解后得到的子问题往往不是互相独立的（即下一个子阶段的求解是建立在上一个子阶段的解的基础上，进行进一步的求解）。

三、适用的情况

能采用动态规划求解的问题的一般要具有3个性质：

（1）最优化原理：如果问题的最优解所包含的子问题的解也是最优的，就称该问题具有最优子结构，即满足最优化原理。

（2）无后效性：即某阶段状态一旦确定，就不受这个状态以后决策的影响。也就是说，某状态以后的过程不会影响以前的状态，只与当前状态有关。

（3）有重叠子问题：即子问题之间是不独立的，一个子问题在下一阶段决策中可能被多次使用到。（该性质并不是动态规划适用的必要条件，但是如果没有这条性质，动态规划算法同其他算法相比就不具备优势）。

四、求解的基本步骤

动态规划所处理的问题是一个多阶段决策问题，一般由初始状态开始，通过对中间阶段决策的选择，达到结束状态。这些决策形成了一个决策序列，同时确定了完成整个过程的一条活动路线(通常是求最优的活动路线)。如图所示。动态规划的设计都有着一定的模式，一般要经历以下几个步骤。

初始状态→│决策１│→│决策２│→…→│决策ｎ│→结束状态

（1）划分阶段：按照问题的时间或空间特征，把问题分为若干个阶段。在划分阶段时，注意划分后的阶段一定要是有序的或者是可排序的，否则问题就无法求解。

（2）确定状态和状态变量：将问题发展到各个阶段时所处于的各种客观情况用不同的状态表示出来。当然，状态的选择要满足无后效性。

（3）确定决策并写出状态转移方程：因为决策和状态转移有着天然的联系，状态转移就是根据上一阶段的状态和决策来导出本阶段的状态。所以如果确定了决策，状态转移方程也就可写出。但事实上常常是反过来做，根据相邻两个阶段的状态之间的关系来确定决策方法和状态转移方程。

（4）寻找边界条件：给出的状态转移方程是一个递推式，需要一个递推的终止条件或边界条件。

一般，只要解决问题的阶段、状态和状态转移决策确定了，就可以写出状态转移方程（包括边界条件）。

实际应用中可以按以下几个简化的步骤进行设计：

（1）分析最优解的性质，并刻画其结构特征。

（2）递归的定义最优解。

（3）以自底向上或自顶向下的记忆化方式（备忘录法）计算出最优值。

（4）根据计算最优值时得到的信息，构造问题的最优解。

五、算法实现的说明

动态规划的主要难点在于理论上的设计，也就是上面4个步骤的确定，一旦设计完成，实现部分就会非常简单。

使用动态规划求解问题，最重要的就是确定动态规划三要素：（1）问题的阶段；（2）每个阶段的状态；（3）从前一个阶段转化到后一个阶段之间的递推关系。

递推关系必须是从次小的问题开始到较大的问题之间的转化，从这个角度来说，动态规划往往可以用递归程序来实现，不过因为递推可以充分利用前面保存的子问题的解来减少重复计算，所以对于大规模问题来说，有递归不可比拟的优势，这也是动态规划算法的核心之处。

确定了动态规划的这三要素，整个求解过程就可以用一个最优决策表来描述，最优决策表是一个二维表，其中行表示决策的阶段，列表示问题状态，表格需要填写的数据一般对应此问题的在某个阶段某个状态下的最优值（如最短路径，最长公共子序列，最大价值等），填表的过程就是根据递推关系，从1行1列开始，以行或者列优先的顺序，依次填写表格，最后根据整个表格的数据通过简单的取舍或者运算求得问题的最优解。

 

实例：动态规划的入门问题——爬楼梯

题目描述：有一座高度是n级台阶的楼梯，从下往上走，每跨一步只能向上1级或者2级台阶。要求用程序来求出一共有多少种走法。

解题思路：

比如，我们走10级的楼梯，每次走1级台阶，一共走10步，这是其中一种走法。我们可以简写成 1,1,1,1,1,1,1,1,1,1。

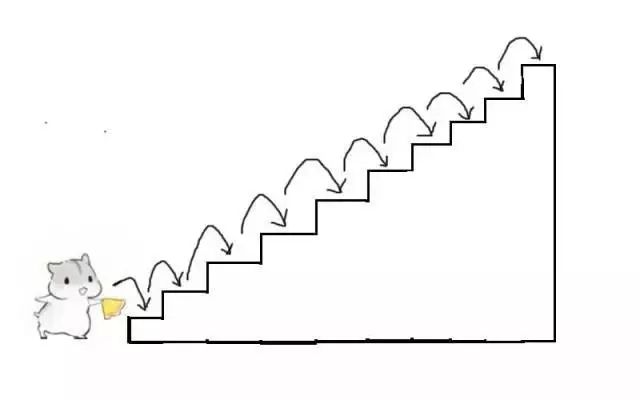
再比如，每次走2级台阶，一共走5步，这是另一种走法。我们可以简写成 2,2,2,2,2。

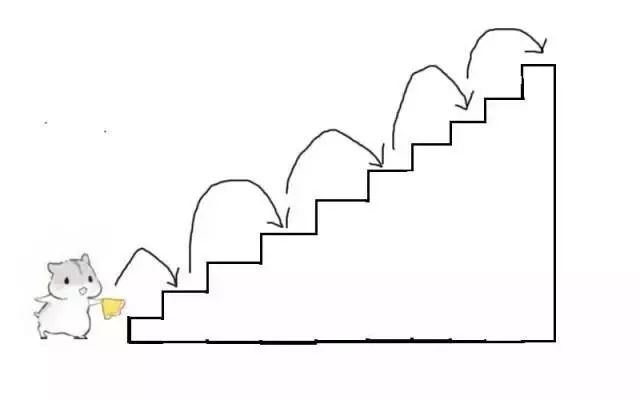
当然，除此之外，还有很多很多种走法。但是这样一个个算太麻烦了，我们可以只去思考最后一步怎么走。

这样，走到第十个楼梯的走法 = 走到第八个楼梯 + 走到第九个楼梯。我们用f(n)来表示走到第n个楼梯的走法，所以就有了f(10) = f(9) + f(8)，然后f(9) = f(8) + f(7)， f(8) = f(7) + f(6)......

这样我们就得出来一个递归式：
f(n) = f(n-1) + f(n-2)

由于在利用动态规划过程中，重复计算过多，所以我们常利用列表存储当前计算结果，避免重复计算。于是，该问题的实现如下（python3.7）：

至此，大家对动态规划算法也算是有了一些初步的了解了，动态规划在日常工作中应用非常广泛，同学们不妨开动脑筋，思考有哪些问题可以利用动态规划的思想来解决。

文源/部分来源于网络

文案/信息学院学生会学术实践部

审核/庞世杰

编辑/章雯