动态规划-2

Posted 2021-04-18 步方糖

题目1:最长公共子序列

分析:

先来看看什么是子串和子序列:

子串应该比较好理解，至于什么是子序列，这里给出一个例子：有两个母串

cnblogs    belong

比如序列bo, bg, lg在母串cnblogs与belong中都出现过并且出现顺序与母串保持一致，我们将其称为公共子序列。最长公共子序列（Longest Common Subsequence,LCS），顾名思义，是指在所有的子序列中最长的那一个。子串是要求更严格的一种子序列，要求在母串中连续地出现。在上述例子的中，最长公共子序列为blog（cnblogs,belong），最长公共子串为lo（cnblogs, belong）。

然后用动态规划的思想分析这道题:用 i , j 分别表示字符串s1和s2中第 i, j 个元素,用二维数组maxlen[i][j]表示从第一个元素分别到第 i, j 个元素的最长公共子序列长度,则有如下关系:

maxlen[i][j] = 0, i=j=0

maxlen[i][j] = maxlen[i-1][j-1] + 1, s1[i] == s2[j]

maxlen[i][j] = max{maxlen[i-1][j], maxlen[i][j-1]}, 其他情况

根据上面关系可以写出以下代码:

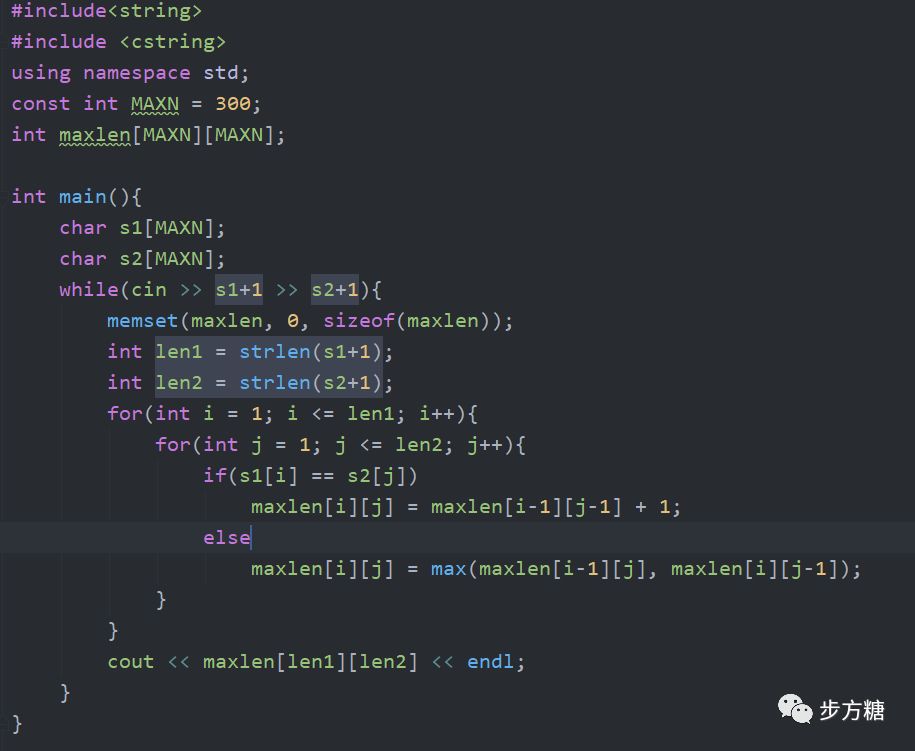
题目2

分析:01背包问题

01背包是指在M件物品取出若干件放在空间为W的背包里，每件物品的体积为W1，W2至Wn，与之相对应的价值为c1,c2至cn。01背包是背包问题中最简单的问题。01背包的约束条件是给定几种物品，每种物品有且只有一个，并且有权值和体积两个属性。在01背包问题中，因为每种物品只有一个，对于每个物品只需要考虑选与不选两种情况。如果不选择将其放入背包中，则不需要处理。如果选择将其放入背包中，由于不清楚之前放入的物品占据了多大的空间，需要枚举将这个物品放入背包后可能占据背包空间的所有情况。

用dp[i][v]表示将第 i 件物品恰好装入容量为v的背包中所能获得的最大价值.对于每一件物品都有放或者不放两种选择,

对于不放入背包,那么问题就变成第 i-1 件物品恰好装入容量为v的背包所能获得的最大价值.即dp[i-1][v]

放入第 i 件物品,那么问题变成第 i-1 件物品恰好放入容量为 v-w[i] 的背包中获得的最大价值 + c[i],即dp[i-1][v-w[i]] + c[i]

那么求dp[i][v]就是两者中最大的那个,即

dp[i][v] = max{dp[i-1][v],dp[i-1][v-w[i]] + c[i]}

由于题目中数据量过大,用二维数组表示dp[i][v]占用空间太大,所以换一种思路表示dp,用dp[v]表示在容量为v的背包内放入若干物品的总价值为dp[v],即dp[v] = max{dp[v], dp[v - w[i]] + c[i]}.这里记住 v 要逆序枚举

题目3:完全背包问题,

有N种物品和一个容量为V的背包，每种物品都有无限件可用。

第i种物品的体积是w，价值是c。求解将哪些物品装入背包可使这些物品的体积总和不超过背包容量，且价值总和最大。

思路:这个问题非常类似于01背包问题，所不同的是每种物品有无限件，也就是从每种物品的角度考虑，与它相关的策略已并非取或不取两种，而是有取0件、取1件、取2件……取[无限]件等很多种。可以得到状态转移方程:

dp[i][v] = max{dp[i-1][v],dp[i][v-w[i]] + c[i]},转换成一维数组的dp形式为dp[v] = max{dp[v], dp[v - w[i]] + c[i]},与01背包相同,不过枚举时是正向枚举.