参赛博文｜0-1背包问题（动态规划）附例题详解——java实现

Posted 2021-04-18 西安比特教育

比特科技

 

问题描述

给定 n 种物品，每种物品有对应的重量weight和价值value，一个容量为 maxWeight 的背包，问：应该如何选择装入背包的物品，使得装入背包中的物品的总价值最大？

思路分析

面对每个物品，我们只有选择拿取或者不拿两种选择，不能选择装入某物品的一部分，也不能装入同一物品多次。

使用动态规划思想，很容易想到，我们需要一个空间来储存：从0号物品开始，对于每个重量上限的最优解。所以我们可以设计一个二维数组存放当前最大价值，如下：（我们假设4件物品，重量和价值数组如下）

Weight[]  = { 2 ,3 ,4 ,5 }    

value[]   = { 3 ,4 ,5 ,7 }      

N = 4 件物品

最大价值数组为maxvalue[N+1][maxWeight+1]，因为我们要从0开始保存

i：只拿前i件物品（这里的i因为取了0，所以对应到weight和value里面都是i-1号位置）      

j：假设能取的总重量为j

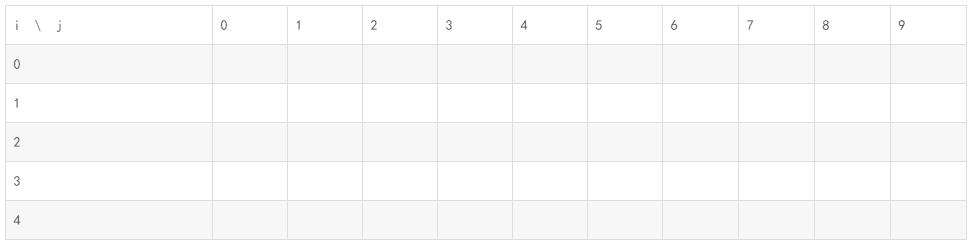
因为当maxWeight = 0 和不取物品（i=0）时，没有任何价值，所以如图先把0填上

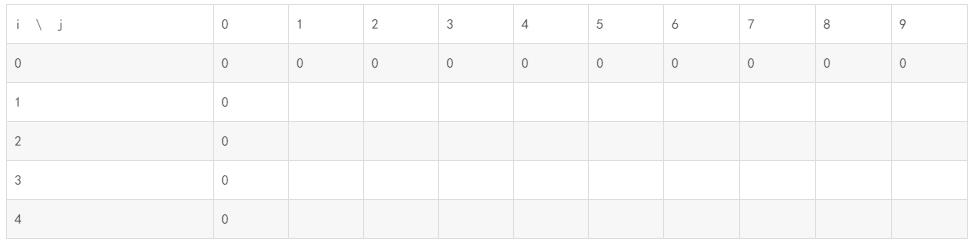
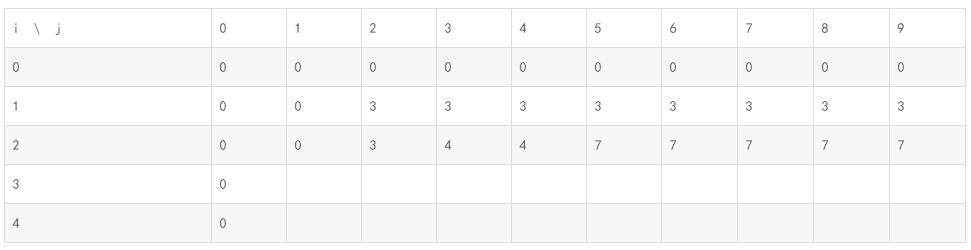
然后我们开始遍历这个表格，填充他们。

我们考虑：开始拿物品的时候，我们判断，如果当前拿到的物品的重量（weight[i-1]）<= 当前能取的最大重量(j)，我们就考虑要不要放进这个。

于是我们比较这两个价值：

maxvalue[i-1][j]（不放这个物品的价值）

value[i-1] + maxvalue[i-1][j-weight[i-1]]（这个物品的价值 加上 当前能放的总重量减去当前物品重量时取前i-1个物品时的对应重量时候的最高价值）

这个是关键，大家仔细想一下

哪个高，我们就吧哪个放进当前数组遍历到的位置。

这里我讲一下，当i=3，的时候的情况

Weight[]=  { 2 ,3 ,4 ,5 }    

value[] =  { 3 ,4 ,5 ,7 }

i=3,j=1: weight[i-1] = 4  <=  j;

所以maxvalue[3][1] = maxvalue[2][1] = 0 ;

i=3,j=2:同理maxvalue[3][2] = maxvalue[2][2] =3;

i=3,j=3:同理maxvalue[3][3] = maxvalue[2][3] =4;

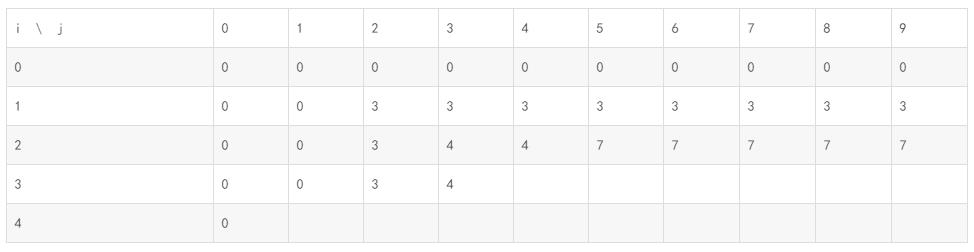
i=3,j=4:

weight[i-1] = 4  <=  j成立;

所以判断

value[i-1] + maxvalue[i-1][j-weight[i-1]]

=5+maxvalue[2][4-4] 

= 5 

比不放入大

所以maxvalue[3][4] = 5;

表示当只有前3件物品，限制重量为4的时候，maxvalue=5

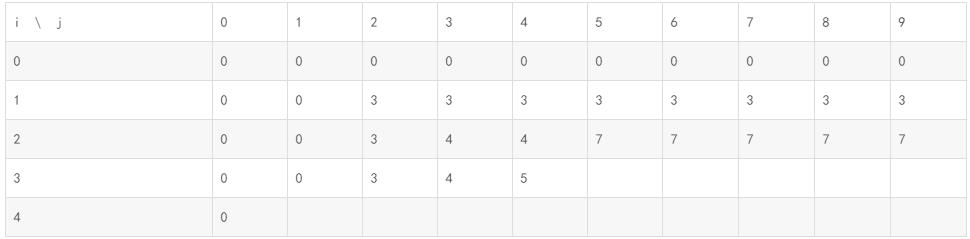
i=3,j=5:

weight[i-1] = 4  <=  j成立;

所以判断value[i-1] + maxvalue[i-1][j-weight[i-1]]

= 5  + maxvalue[2][5-4]

= 5  +  0   

比maxvalue[i-1][j] 小

所以maxvalue[3][5] = maxvalue[i-1][j] = maxvalue[2][5]  =  7;

表示当只有前3件物品，限制重量为5的时候，maxvalue=7

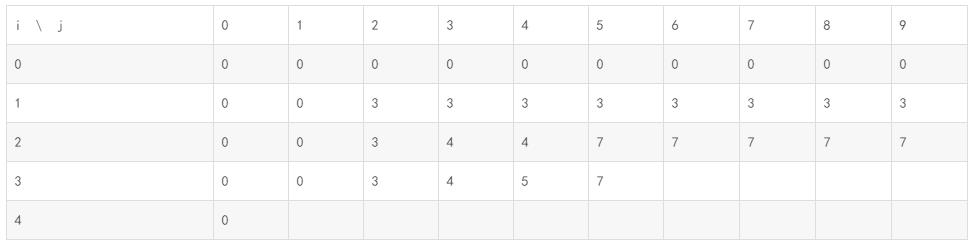
i=3,j=6:

weight[i-1] = 4  <=  j 成立;

所以判断value[i-1] + maxvalue[i-1][j-weight[i-1]]

= 5 +  maxvalue[2][6-4]

= 5  + 3   

比maxvalue[i-1][j] 大

所以maxvalue[3][6]  =  8;

表示当只有前3件物品，限制重量为6的时候，maxvalue=8

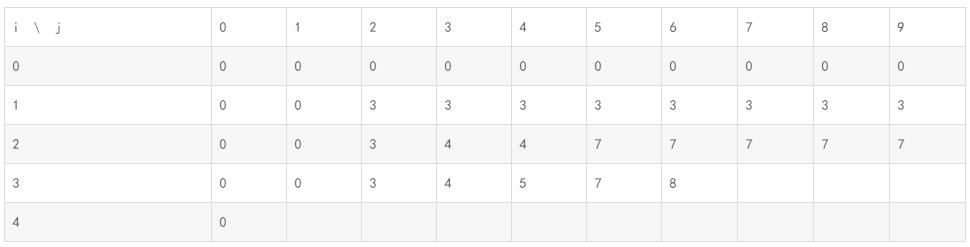
后面依次类推，所有的情况我都讲到了

最后的表填完后：

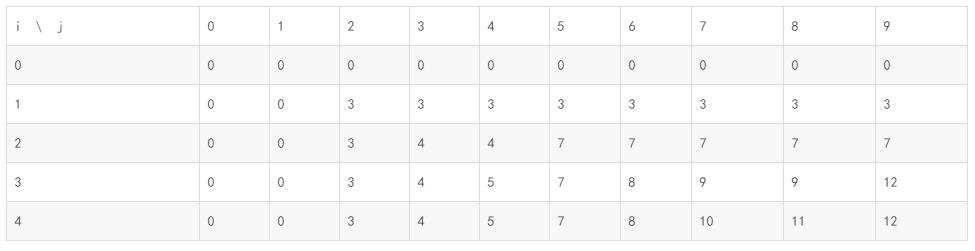
直接输出右下角就是最大价值。

代码如下：

package 动态规划;
//0-1背包问题
public class Knapsack {
 
 public static int knapsack(int[] weight, int[] value, int maxweight){

   int n = weight.length;
   //最大价值数组为maxvalue[N+1][maxWeight+1]，因为我们要从0开始保存
   int[][] maxvalue = new int[n+1][maxweight + 1];
   
   //重量和物品为0时，价值为0
   for (int i = 0; i < maxweight + 1; i++) {
     maxvalue[0][i] = 0;
     
   }
   for (int i = 0; i < n + 1; i++) {
     maxvalue[i][0] = 0;
     
   }
   
   //i：只拿前i件物品（这里的i因为取了0，所以对应到weight和value里面都是i-1号位置）      
    //j：假设能取的总重量为j
   //n是物品件数
   for (int i = 1; i <= n ; i++) {
     for (int j = 1; j <= maxweight; j++) {
       //当前最大价值等于放上一件的最大价值
       maxvalue[i][j] = maxvalue[i-1][j];
       //如果当前件的重量小于总重量，可以放进去或者拿出别的东西再放进去
        if (weight[i-1] <= j) {
         //比较（不放这个物品的价值）和
         //（这个物品的价值 加上 当前能放的总重量减去当前物品重量时取前i-1个物品时的对应重量时候的最高价值）
          if(maxvalue[i-1][j - weight[i-1]] + value[i-1]>maxvalue[i-1][j]) {
            maxvalue[i][j] = maxvalue[i-1][j - weight[i-1]] + value[i-1];
          }
       }
     }
   }
   return maxvalue[n][maxweight];
 }
 public static void main(String[] args) {
   // TODO 自动生成的方法存根
   int weight[] = {2,3,4,5};
   int value[] = {3,4,5,7};
   int maxweight = 9;
   System.out.println(knapsack(weight, value, maxweight));
 }

}

如果你喜欢这篇文章

请继续关注博文大赛

为你喜欢的作者打call哦！

End

---

编辑：啊琛琛

审核：啊琛琛

导师微信 / 15596668826

导师QQ / 2799935869

导师Tel / 15249287076