动态规划算法秘籍
Posted 数据结构与算法
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了动态规划算法秘籍相关的知识,希望对你有一定的参考价值。
作者丨rainchxy
https://www.jianshu.com/p/0e2d0494593a
本文来自通俗易懂算法入门书《趣学算法》。
动态规划是1957年理查德·贝尔曼在《Dynamic Programming》一书中提出来的,八卦一下,这个人可能有同学不知道,但他的一个算法你可能听说过,他和莱斯特·福特一起提出了求解最短路径的Bellman-Ford 算法,该算法解决了Dijkstra算法不能处理负权值边的问题。
Dynamic Programming,这里的Programming不是编程的意思,而是指一种表格处理法。我们把每一步得到的子问题结果存储在表格里,每次遇到该子问题时不需要再求解一遍,只需要查询表格即可。
4.1.1 算法思想
动态规划也是一种分治思想,但与分治算法不同的是,分治算法是把原问题分解为若干子问题,自顶向下,求解各子问题,合并子问题的解从而得到原问题的解。动态规划也是把原问题分解为若干子问题,然后自底向上,先求解最小的子问题,把结果存储在表格中,在求解大的子问题时,直接从表格中查询小的子问题的解,避免重复计算,从而提高算法效率。
 4.1.2 算法要素
4.1.2 算法要素
什么问题可以使用动态规划呢?我们首先要分析问题是否具有以下两个性质:
(1)最优子结构
最优子结构性质是指问题的最优解包含其子问题的最优解。最优子结构是使用动态规划的最基本条件,如果不具有最优子结构性质就不可以使用动态规划解决。
(2)子问题重叠
子问题重叠是指在求解子问题的过程中,有大量的子问题是重复的,那么只需要求解一次,然后把结果存储在表中,以后使用时可以直接查询,不需要再次求解。子问题重叠不是使用动态规划的必要条件,但问题存在子问题重叠更能够充分彰显动态规划的优势。
什么问题可以使用动态规划呢?我们首先要分析问题是否具有以下两个性质:
(1)最优子结构
最优子结构性质是指问题的最优解包含其子问题的最优解。最优子结构是使用动态规划的最基本条件,如果不具有最优子结构性质就不可以使用动态规划解决。
(2)子问题重叠
子问题重叠是指在求解子问题的过程中,有大量的子问题是重复的,那么只需要求解一次,然后把结果存储在表中,以后使用时可以直接查询,不需要再次求解。子问题重叠不是使用动态规划的必要条件,但问题存在子问题重叠更能够充分彰显动态规划的优势。
 4.1.1 解题秘籍
4.1.1 解题秘籍
遇到一个实际问题,如何采用动态规划来解决呢?
(1) 分析最优解的结构特征。
(2) 建立最优值的递归式。
(3) 自底向上计算最优值,并记录。
(4) 构造最优解。
本章通过8个实例,讲解了动态规划的解题过程。动态规划求解最优化问题时需要考虑两个性质:最优子结构和子问题重叠,只要满足最优子结构性质就可以使用动态规划,如果还具有子问题重叠,则更能彰显动态规划的优势。判断可以使用动态规划后,就可以分析其最优子结构特征,找到原问题和子问题的关系,从而得到最优解递归式。然后按照最优解递归式自底向上求解,采用备忘机制(查表法)有效解决子问题重叠,重复的子问题不需要重复求解,只需查表即可。
动态规划的关键:
(1)最优子结构判定
a. 作出一个选择;
b. 假定已经知道了哪种选择是最优的;
例如矩阵连乘问题,我们假设已经知道在第k个矩阵加括号是最优的,即(AiAi+1…Ak)(Ak+1Ak+2…Aj)。
c. 最优选择后会产生哪些子问题;
例如矩阵连乘问题,我们作出最优选择后产生两个子问题:(AiAi+1…Ak),(Ak+1Ak+2…Aj)。
d. 证明原问题的最优解包含其子问题的最优解。
通常使用“剪切—粘贴”反证法。证明如果原问题的解是最优解,那么子问题的解也是最优解。反证:假定子问题的解不是最优解,那么就可以将它“剪切”掉,把最优解“粘贴”进去,从而得到一个比原问题最优解更优的解,这与前提原问题的解是最优解矛盾。得证。
例如:矩阵连乘问题,c=a+b+d,我们只需要证明如果c是最优的,则a和b一定是最优的(即原问题的最优解包含子问题的最优解)。
反证法:如果a不是最优的,(AiAi+1…Ak) 存在一个最优解aˊ,aˊ
(2)如何得到最优解递归式
a.分析原问题最优解和子问题最优解的关系;
例如矩阵连乘问题,我们假设已经知道在第k个矩阵加括号是最优的,即(AiAi+1…Ak)(Ak+1Ak+2…Aj)。作出最优选择后产生两个子问题:(AiAi+1…Ak),(Ak+1Ak+2…Aj)。如果我们用m[i][j]表示AiAi+1…Aj矩阵连乘的最优解,那么两个子问题:(AiAi+1…Ak),(Ak+1Ak+2…Aj)对应的最优解分别是m[i][k],m[k+1][j]。剩下的只需要考察(AiAi+1…Ak)和(Ak+1Ak+2…Aj)的结果矩阵相乘的乘法次数了。两个结果矩阵相乘的乘法次数是pi*pk+1*qj。
因此,原问题最优解和子问题最优解的关系:m[i][j]= m[i][k]+m[k+1][j]+ pi*pk+1*qj
b.考察有多少种选择;
实质上,我们并不知道哪种选择是最优的,因此就需要考察有多少种选择,然后从这些选择中找到最优解。
例如矩阵连乘问题,加括号的位置k(AiAi+1…Ak)(Ak+1Ak+2…Aj),k的取值范围是{i,i+1,…,j-1},即i≤k
c.得到最优解递归式。
例如矩阵连乘问题,m[i][j]表示AiAi+1…Aj矩阵连乘的最优解,根据最优解和子问题最优解的关系,并考察所有的选择,找到最小值就是我们要的最优解。
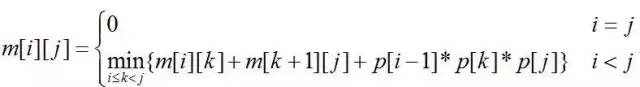
推荐↓↓↓
长
按
关
注
以上是关于动态规划算法秘籍的主要内容,如果未能解决你的问题,请参考以下文章 算法动态规划 ② ( 动态规划四要素 | 动态规划状态 State | 动态规划初始化 Initialize | 动态规划方程 Function | 动态规划答案 Answer ) 算法动态规划 ② ( 动态规划四要素 | 动态规划状态 State | 动态规划初始化 Initialize | 动态规划方程 Function | 动态规划答案 Answer ) 算法动态规划 ① ( 动态规划简介 | 自底向上的动态规划示例 | 自顶向下的动态规划示例 )