算法系列之-动态规划

Posted 2021-04-18 三木小小推

文章引用自：

https://blog.csdn.net/u013309870/article/details/75193592

动态规划算法的核心

A * "1+1+1+1+1+1+1+1 =？" *
A : "上面等式的值是多少"
B : 计算 "8!"
A *在上面等式的左边写上 "1+" *
A : "此时等式的值为多少"
B : quickly "9!"
A : "你怎么这么快就知道答案了"
A : "只要在8的基础上加1就行了"
A : "所以你不用重新计算因为你记住了第一个等式的值为8!动态规划算法也可以说是 '记住求过的解来节省时间'"

由上面的小故事可以知道动态规划算法的核心就是记住已经解决过的子问题的解。

动态规划算法的两种形式

上面已经知道动态规划算法的核心是记住已经求过的解，记住求解的方式有两种：①自顶向下的备忘录法 ②自底向上。 为了说明动态规划的这两种方法，举一个最简单的例子：求斐波拉契数列Fibonacci 。先看一下这个问题：

Fibonacci (n) = 1;   n = 0
Fibonacci (n) = 1;   n = 1
Fibonacci (n) = Fibonacci(n-1) + Fibonacci(n-2)

以前学c语言的时候写过这个算法使用递归十分的简单。先使用递归版本来实现这个算法：

 1 public int fib(int n)
 2{
 3    if(n<=0)
 4        return 0;
 5    if(n==1)
 6        return 1;
 7    return fib( n-1)+fib(n-2);
 8}
 9//输入6
10//输出：8

先来分析一下递归算法的执行流程，假如输入6，那么执行的递归树如下：

上面的递归树中的每一个子节点都会执行一次，很多重复的节点被执行，fib(2)被重复执行了5次。由于调用每一个函数的时候都要保留上下文，所以空间上开销也不小。这么多的子节点被重复执行，如果在执行的时候把执行过的子节点保存起来，后面要用到的时候直接查表调用的话可以节约大量的时间。下面就看看动态规划的两种方法怎样来解决斐波拉契数列Fibonacci 数列问题。

①自顶向下的备忘录法

 1public static int Fibonacci(int n)
 2{
 3        if(n<=0)
 4            return n;
 5        int []Memo=new int[n+1];        
 6        for(int i=0;i<=n;i++)
 7            Memo[i]=-1;
 8        return fib(n, Memo);
 9    }
10    public static int fib(int n,int []Memo)
11    {
12
13        if(Memo[n]!=-1)
14            return Memo[n];
15    //如果已经求出了fib（n）的值直接返回，否则将求出的值保存在Memo备忘录中。               
16        if(n<=2)
17            Memo[n]=1;
18
19        else Memo[n]=fib( n-1,Memo)+fib(n-2,Memo);  
20
21        return Memo[n];
22    }

备忘录法也是比较好理解的，创建了一个n+1大小的数组来保存求出的斐波拉契数列中的每一个值，在递归的时候如果发现前面fib（n）的值计算出来了就不再计算，如果未计算出来，则计算出来后保存在Memo数组中，下次在调用fib（n）的时候就不会重新递归了。比如上面的递归树中在计算fib（6）的时候先计算fib（5），调用fib（5）算出了fib（4）后，fib（6）再调用fib（4）就不会在递归fib（4）的子树了，因为fib（4）的值已经保存在Memo[4]中。

②自底向上的动态规划

备忘录法还是利用了递归，上面算法不管怎样，计算fib（6）的时候最后还是要计算出fib（1），fib（2），fib（3）……,那么何不先计算出fib（1），fib（2），fib（3）……,呢？这也就是动态规划的核心，先计算子问题，再由子问题计算父问题。

 1public static int fib(int n)
 2{
 3        if(n<=0)
 4            return n;
 5        int []Memo=new int[n+1];
 6        Memo[0]=0;
 7        Memo[1]=1;
 8        for(int i=2;i<=n;i++)
 9        {
10            Memo[i]=Memo[i-1]+Memo[i-2];
11        }       
12        return Memo[n];
13}

自底向上方法也是利用数组保存了先计算的值，为后面的调用服务。观察参与循环的只有 i，i-1 , i-2三项，因此该方法的空间可以进一步的压缩如下。

 1public static int fib(int n)
 2    {
 3        if(n<=1)
 4            return n;
 5
 6        int Memo_i_2=0;
 7        int Memo_i_1=1;
 8        int Memo_i=1;
 9        for(int i=2;i<=n;i++)
10        {
11            Memo_i=Memo_i_2+Memo_i_1;
12            Memo_i_2=Memo_i_1;
13            Memo_i_1=Memo_i;
14        }       
15        return Memo_i;
16    }

一般来说由于备忘录方式的动态规划方法使用了递归，递归的时候会产生额外的开销，使用自底向上的动态规划方法要比备忘录方法好。 你以为看懂了上面的例子就懂得了动态规划吗？那就too young too simple了。动态规划远远不止如此简单，下面先给出一个例子看看能否独立完成。然后再对动态规划的其他特性进行分析。

动态规划小试牛刀

例题：钢条切割

上面的例题来自于算法导论 关于题目的讲解就直接截图算法导论书上了这里就不展开讲。现在使用一下前面讲到三种方法来来实现一下。

①递归版本

 1price = [1, 5, 8, 9, 10, 17, 17, 20, 24, 30]
 2
 3def cut(p, n):
 4
 5    if n == 0:
 6        return 0
 7    q = 0
 8    for i in range(1, n+1):
 9        q = max(q, p[i-1]+cut(p, n-i))
10    return q

递归很好理解，如果不懂可以看上面的讲解，递归的思路其实和回溯法是一样的，遍历所有解空间但这里和上面斐波拉契数列的不同之处在于，在每一层上都进行了一次最优解的选择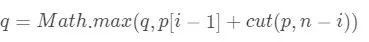，这个段语句就是最优解选择，这里上一层的最优解与下一层的最优解相关。

②备忘录版本

 1public static int cutMemo(int []p)
 2    {
 3        int []r=new int[p.length+1];
 4        for(int i=0;i<=p.length;i++)
 5            r[i]=-1;                        
 6        return cut(p, p.length, r);
 7    }
 8    public static int cut(int []p,int n,int []r)
 9    {
10        int q=-1;
11        if(r[n]>=0)
12            return r[n];
13        if(n==0)
14            q=0;
15        else {
16            for(int i=1;i<=n;i++)
17                q=Math.max(q, cut(p, n-i,r)+p[i-1]);
18        }
19        r[n]=q;
20
21        return q;
22    }

有了上面求斐波拉契数列的基础，理解备忘录方法也就不难了。备忘录方法无非是在递归的时候记录下已经调用过的子函数的值。这道钢条切割问题的经典之处在于自底向上的动态规划问题的处理，理解了这个也就理解了动态规划的精髓。

③自底向上的动态规划

 1len_stick = 4
 2max_price = [0 for i in range(len_stick+1)]
 3
 4for k in range(1, len_stick+1):
 5     max_price[k] = 0
 6     for i in range(1, k+1):
 7         temp_price = price[i-1] + max_price[k-i]
 8         if temp_price > max_price[k]:
 9             max_price[k] = temp_price
10
11
12print(max_price[len_stick])

自底向上的动态规划问题中最重要的是理解注释①处的循环，这里外面的循环是求r[1],r[2]……，里面的循环是求出r[1],r[2]……的最优解，也就是说r[i]中保存的是钢条长度为i时划分的最优解，这里面涉及到了最优子结构问题，也就是一个问题取最优解的时候，它的子问题也一定要取得最优解。下面是长度为4的钢条划分的结构图。我就偷懒截了个图。

动态规划原理

虽然已经用动态规划方法解决了上面两个问题，但是大家可能还跟我一样并不知道什么时候要用到动态规划。总结一下上面的斐波拉契数列和钢条切割问题，发现两个问题都涉及到了重叠子问题，和最优子结构。

①最优子结构

用动态规划求解最优化问题的第一步就是刻画最优解的结构，如果一个问题的解结构包含其子问题的最优解，就称此问题具有最优子结构性质。因此，某个问题是否适合应用动态规划算法，它是否具有最优子结构性质是一个很好的线索。使用动态规划算法时，用子问题的最优解来构造原问题的最优解。因此必须考查最优解中用到的所有子问题。

②重叠子问题

在斐波拉契数列和钢条切割结构图中，可以看到大量的重叠子问题，比如说在求fib（6）的时候，fib（2）被调用了5次，在求cut（4）的时候cut（0）被调用了4次。如果使用递归算法的时候会反复的求解相同的子问题，不停的调用函数，而不是生成新的子问题。如果递归算法反复求解相同的子问题，就称为具有重叠子问题（overlapping subproblems）性质。在动态规划算法中使用数组来保存子问题的解，这样子问题多次求解的时候可以直接查表不用调用函数递归。

欢迎订阅

下面是三木小小推的二维码，欢迎订阅呦~~

你点的每个好看，我都认真当成了喜欢