动态规划——数字三角形

Posted 2021-04-18 coding易码当先

1

问题描述

        如下图所示，一只蚂蚁从顶层数字 13 往底层数字爬行，这只蚂蚁在顶层数字 13 时，只能往左下数字 11 或者右下数字 8 走。给定一个 n 层的数字三角形，求出此蚂蚁从顶层数字走到底层数字时所经过的所有数字之和的最大值。

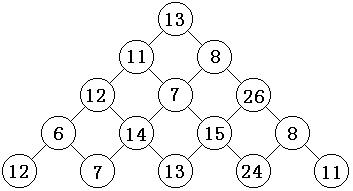
图1 数字三角形

2

问题分析

        

        如图 1 所示，要求数字 13 到底层数字之和的最大值，就相当于找出从数字 11 到底层数字之和的最大值以及从数字 8 到底层数字之和的最大值两者中的最大值再加上自身的值。假设使用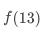表示数字 13 从顶层到底层数字之和的最大值，那么就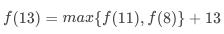。而对于底层数字来说，有。

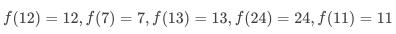3

数据存储

        

        数字三角形如何存储呢？ 我们可以使用一个二维矩阵来存储，如下代码所示。

total_rows = 5 # 总行数
digit = [[13],
         [11,8],
         [12,7,26],
         [6,14,15,8],
         [12,7,13,24,11]]

4

列出数学递推公式

        

        按照上述方式存储之后，依据我们之前的问题分析，对于第 i 行第 j 列的数字，其到底层数字之和最大值可以表示。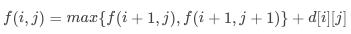

5

使用递归的方式实现

        

        递归实现的代码如下：

def f(row, column):
    if row is total_rows - 1:
        return digit[row][column]
    else:
        return max(f(row+1, column), f(row+1, column+1)) + digit[row][column]

        但是使用递归的方式来实现的话，当层数比较大的时候我们会发现运算起来相当的慢，因为递归里面出现了大量的重复计算。

6

动态规划

        使用数组把已经计算过的结果保存下来，避免了重复计算，能够极大的提升计算的速度。

def find_max(rows, columns):
    rows -= 2
    columns -= 2
    for row in range(rows, -1, -1):
        for column in range(0, columns + 1):
            digit[row][column] = max(digit[row + 1][column], digit[row + 1][column + 1]) + digit[row][column]
        columns -= 1
    return digit[0][0]