用这个例子理解动态规划，怎么可能不懂？

Posted 2021-04-18 Python那些事

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了用这个例子理解动态规划，怎么可能不懂？相关的知识，希望对你有一定的参考价值。

豆豆家住2楼，每天需要爬10级楼梯，每次走1级或2级，请问爬到2楼一共有多少种走法？

比如，每次走1级台阶，一共走10步，这是其中一种走法。我们可以简写成 1,1,1,1,1,1,1,1,1,1。再比如，每次走2级台阶，一共走5步，这是另一种走法。我们可以简写成 2,2,2,2,2。当然，除此之外，还有很多很多种走法。

可以从最后一步考虑：当走到最后一步的时候，可能有几种情况？

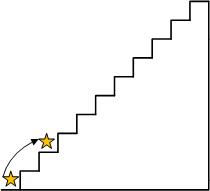
因为每次只能走1级或两级，所以最后一步肯定是从9级到第10级或者第8级到第10级，故只有如下图所示的两种方案。

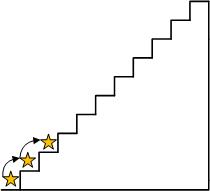
用这个例子理解动态规划，怎么可能不懂？

那么，再考虑一个问题，如果从第0级到第9级一共有X种走法，从第0级到第8级一共有Y种走法，那么从第0级到第10级一共有多少种走法？

很明显，走到第10级台阶分为两种情况，先到第9级，共有X种走法，或者先到第8级，共有Y种走法，那么总共共有X+Y种走法。

为了表达方便，我们把10级台阶走法的数量记录为F(10)，9级台阶走法的数量记录为F(9)，8级台阶走法的数量记录为F(8)，则有：F(10) = F(9) + F(8)。递推之后，当剩余1级台阶和2级台阶时，分别由多少种走法呢？很明显，F(1) = 1, F(2) = 2。

用这个例子理解动态规划，怎么可能不懂？

所以，将问题建立模型为：

F(1) = 1

F(2) = 2

F(n) = F(n-1) + F(n-2) (3 <= n <= 10)

方案1：递归式动态规划

现在让我们看一下动态规划，它采用分治的策略，把求最优解问题分解为求若干子问题的最优解，记录子问题的解，化繁为简。

Python代码如下：

def climbStairs(n):
    """
 计算n级台阶的走法，每次可走1步或者2步
 :param n: 台阶总数
 :return: n级台阶的走法
 """
    if n < 1:
        return 0
    elif n == 1:
        return 1
    elif n == 2:
        return 2
    else:
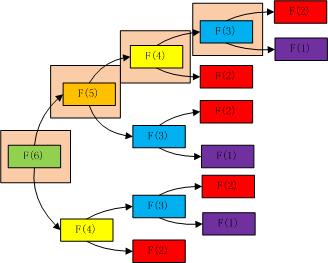
        return climbStairs(n - 1) + climbStairs(n - 2)

很明显，递归算法的缺点是耗时严重，存在大量的重复计算（如下图所示只需要计算阴影部分的即可），算法复杂度高（算法复杂度为O(2^n)）。

用这个例子理解动态规划，怎么可能不懂？

方案2：备忘录递归式动态规划

那么如何避免呢？可以通过备忘录算法，即每次计算出的n级台阶的走法都存储起来，下次用的时候，如果有，则直接使用，不再计算。Python代码如下：

def climbStairs(n, value):
    """
 计算n级台阶的走法，每次可走1步或者2步
 :param n: 台阶总数
 :param value: 存储各个不同台阶走法的dict
 :return: n级台阶的走法
 """
    if n < 1:
        return 0
    elif n == 1:
        return 1
    elif n == 2:
        return 2
    else:
        if value.get(n) is not None:
            return value.get(n)
        else:
            return climbStairs(n - 1, value) + climbStairs(n - 2, value)

通过备忘录算法，算法复杂度变为O(n)，而空间复杂度也是O(n)。怎么进行进一步的简化呢？

方案3：迭代求解

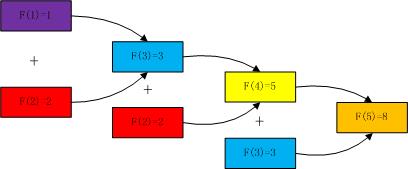
刚刚我们是逆向思考，从最后一步开始思考。现在，我们反过来，从第1,2步开始思考。当我们知道F(1)和F(2)后，可以推知F(3)的值，同理，F(4)的值可以由F(2)和F(3)得知。

用这个例子理解动态规划，怎么可能不懂？

你发现了什么？没错，正向思考只需要保存邻近2个解。Python代码如下：

def climbStairs(n):
    """
 计算n级台阶的走法，每次可走1步或者2步
 :param n: 台阶总数
 :return: n级台阶的走法
 """
    if n < 1:
        return 0
    if n == 1:
        return 1
    if n == 2:
        return 2

    a = 1
    b = 2
    temp = 0

    for i in range(3,n + 1):
        temp = a + b
        a = b
        b = temp
    return temp