动态规划类算法——最优字典序
Posted 斯年有归
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了动态规划类算法——最优字典序相关的知识,希望对你有一定的参考价值。
算法
题源中国计算机协会——计算机职业资格认证考试
试题编号:201612-4
试题名称:压缩编码
时间限制:3.0s
内存限制:256.0MB

要求描述


算法分析

由于要保持字典序 此算法并不适用于哈夫曼算法
却似乎可以用类似哈夫曼的思想解决:
保持字典序 寻找并与最小的相邻节点合并成树
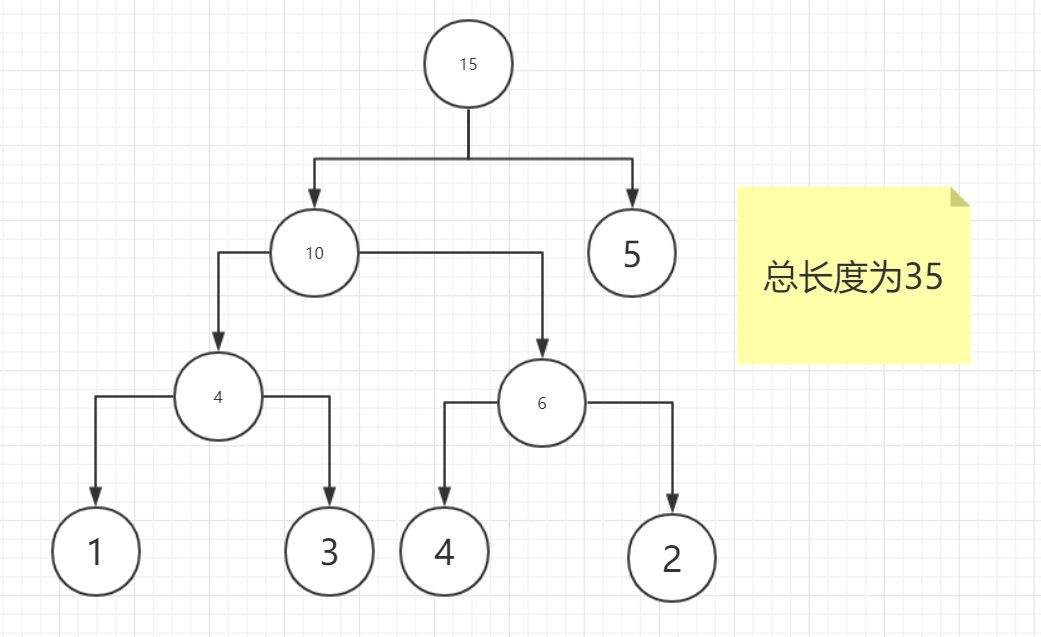
但是这显然不是最优解
最优解题目已给出如下
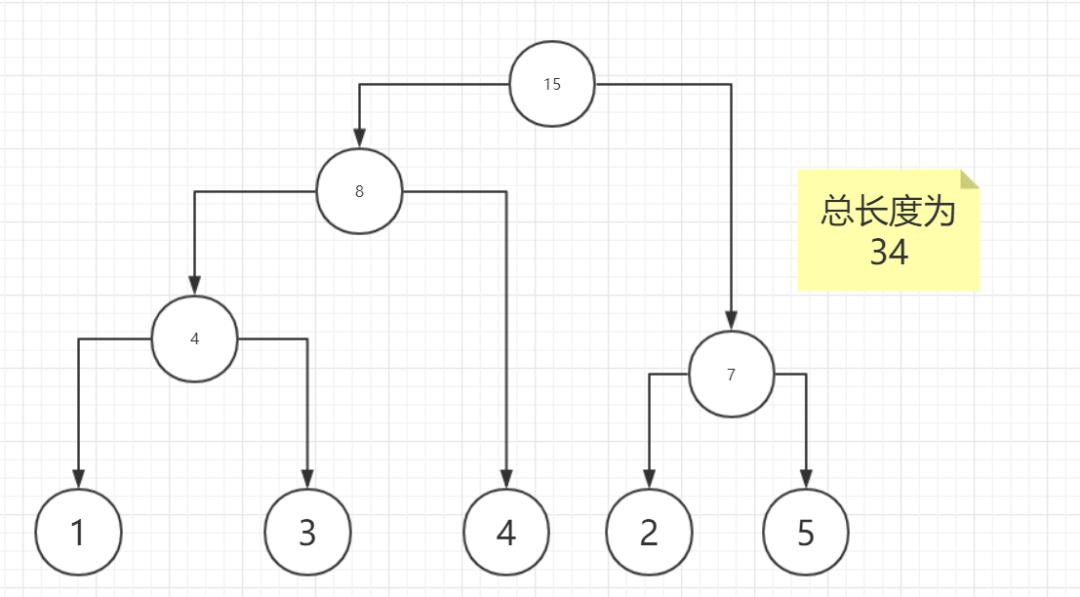
故知这题属于动态规划类算法
而非贪心类算法
解决方案

设元素为n个 则建立一个nxn的矩阵
矩阵元素(i,j)表示从i到j字母的最短长度
——局部的最优结果
对角线元素为对应字母的频率
(同时也符合上句的定义)

下一步是列举出两两相邻的两个点的最短长度
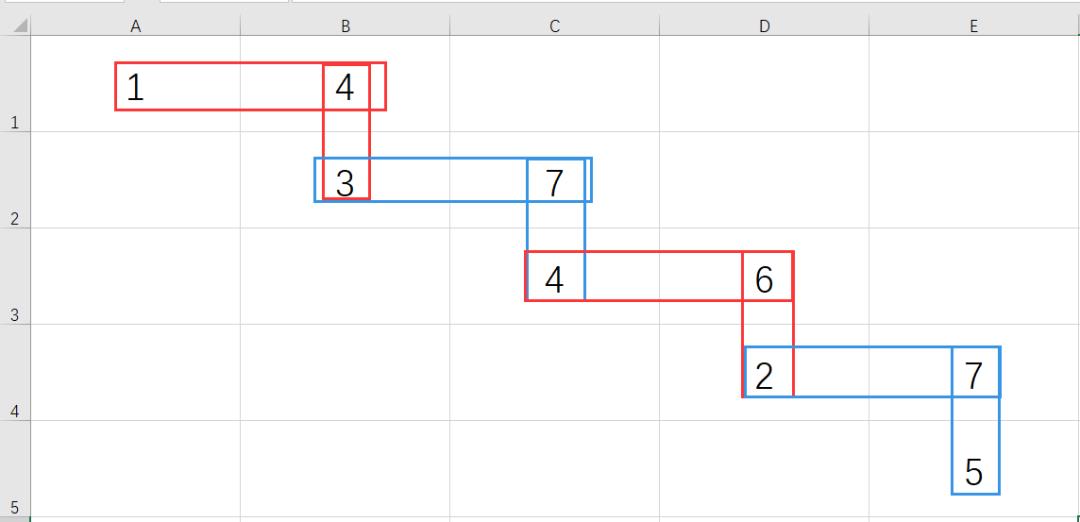
接着下一步/层(此步开始详细说明原理)
(1,C)就是A-C字典序的最优长度
有可能的情况是:
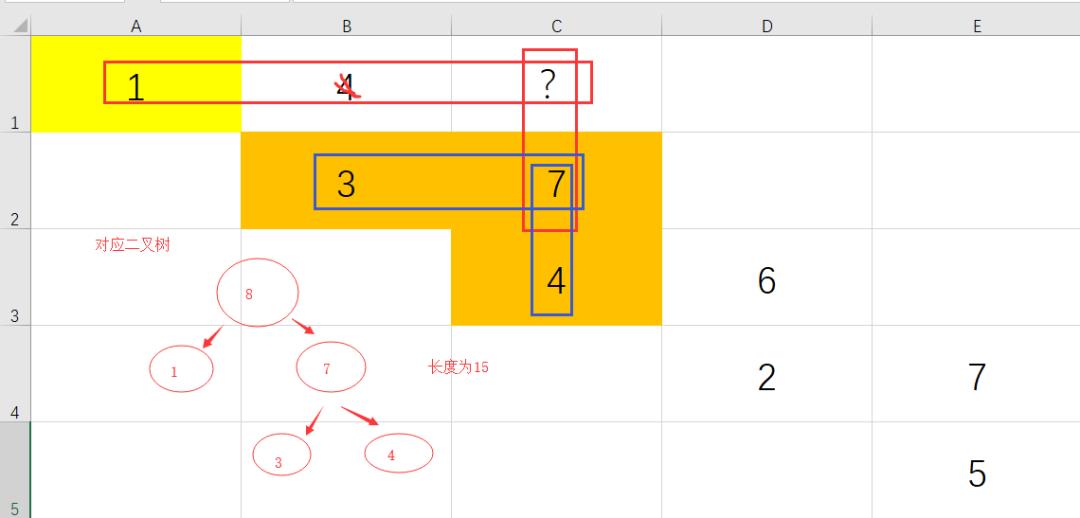
情况1
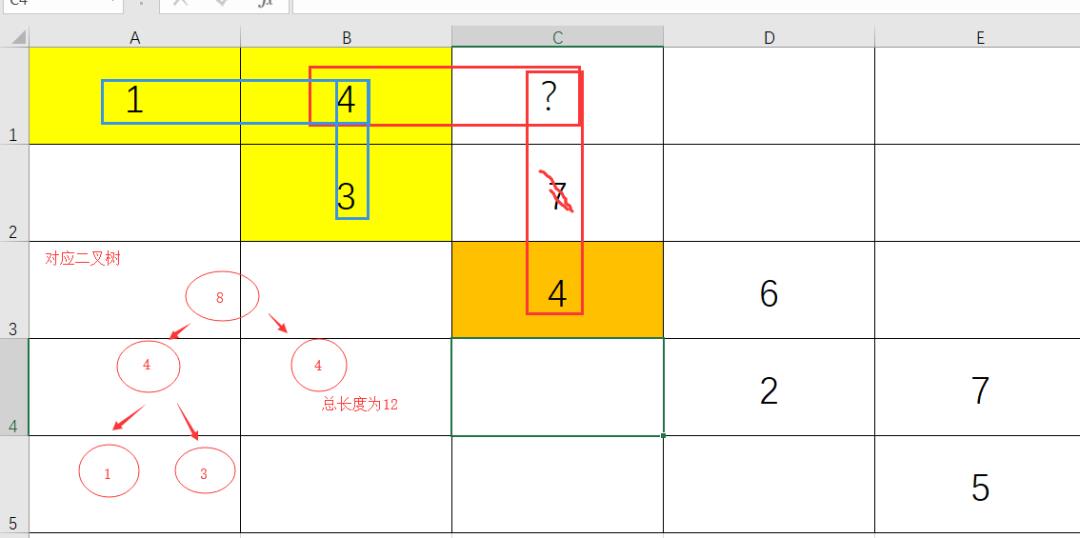
情况2
故(1,C)的局部最优解是情况2 总长度为12
同理填满这一层
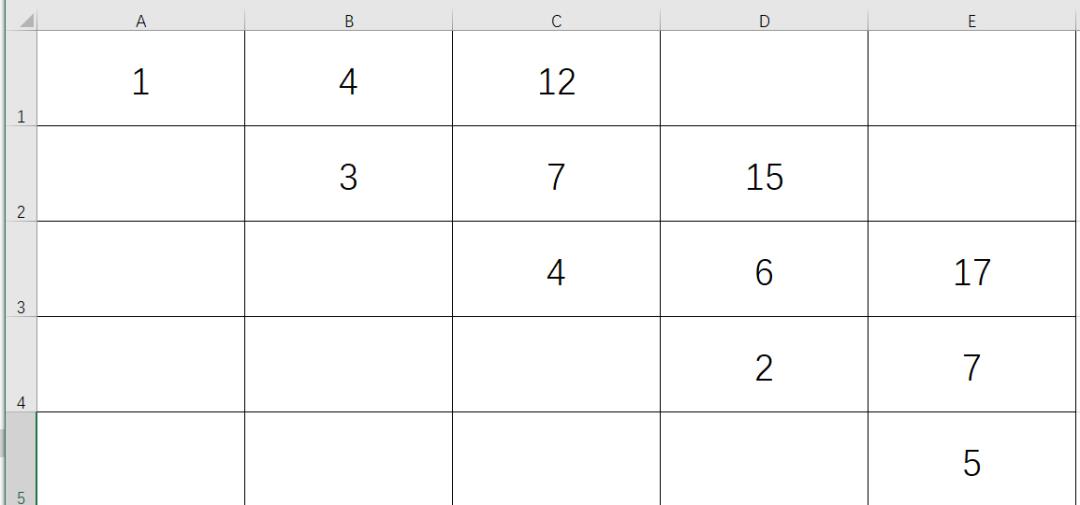
下一层用同样的方法
这里直接给出最短长度的方案
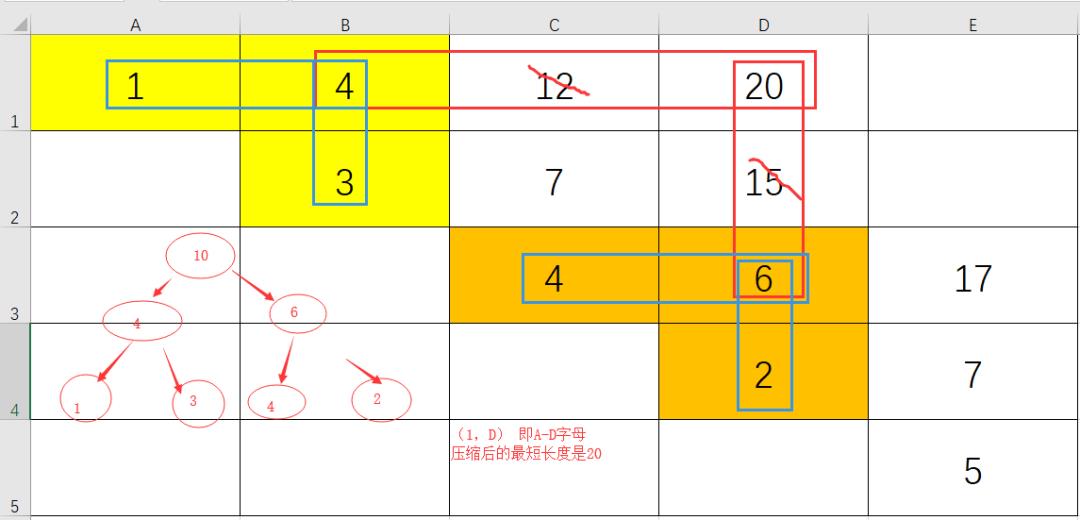
例子中的最终答案
即由A-E,点(1,E)的结果如下
代码实现
import java.util.*;
public class Main
{
static public void main(String[] args)
{
Scanner sc=new Scanner(System.in);
int n=sc.nextInt();
int[][] shu=new int[n][n];
for(int i=0;i<n;i++)
{
shu[i][i]=sc.nextInt();
}
// System.out.println("开始执行");
int min=0;
int x=0;
int y=0;
int sum=0;
for(int i=1;i<n;i++)
{
for(int j=0;j<n-i;j++)
{
min=1<<30;//最大值
x=0;
y=0;
sum=0;
for(int k=j;k<i+j;k++)
{
x=shu[j][k];
y=shu[k+1][i+j];
if(k==j)
{
x=0;
}
if(k+1==j+i)
{
y=0;
}
if(min>x+y) min=x+y;
}
//求出最小的组合边后,入加sum
for(int u=j;u<=i+j;u++)
{
sum+=shu[u][u];
}
shu[j][i+j]=sum+min;
}
}
// System.out.println("矩阵::");
// for(int h=0;h<n;h++)
// { for(int g=0;g<n;g++)
// {
// System.out.print(shu[h][g]+" ");
// }
// System.out.println(" ");
// }
System.out.println(shu[0][n-1]);//"输出结果:"
}
}
算法:Parkz
排版:Cecilia
ABOUT US
随缘post算法
欢迎一起探讨及错误指正
以上是关于动态规划类算法——最优字典序的主要内容,如果未能解决你的问题,请参考以下文章