经典动态规划:打家劫舍系列问题
Posted 数据结构与算法
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了经典动态规划:打家劫舍系列问题相关的知识,希望对你有一定的参考价值。
作者丨labuladong
House Robber I
public int rob(int[] nums);
// 主函数
public int rob(int[] nums) {
return dp(nums, 0);
}
// 返回 nums[start..] 能抢到的最大值
private int dp(int[] nums, int start) {
if (start >= nums.length) {
return 0;
}
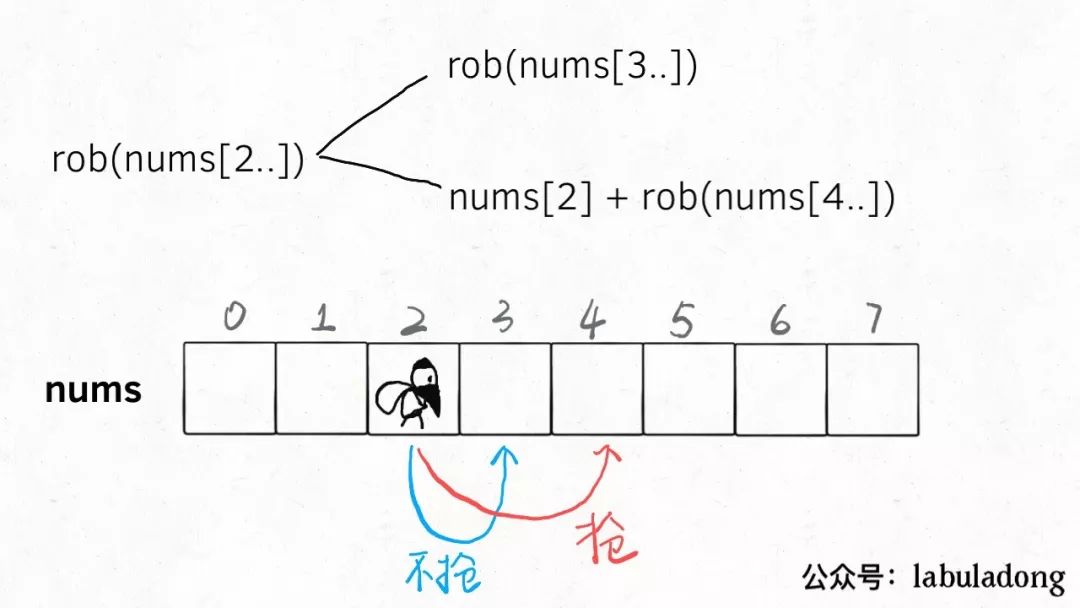
int res = Math.max(
// 不抢,去下家
dp(nums, start + 1),
// 抢,去下下家
nums[start] + dp(nums, start + 2)
);
return res;
}
start
位置,是存在重叠子问题的,比如下图:
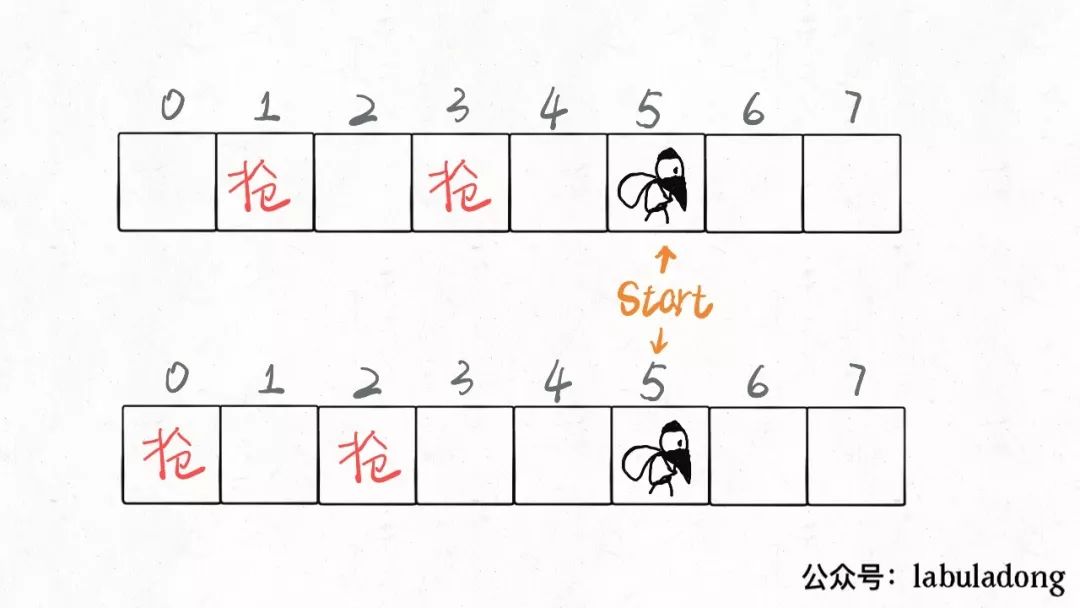
private int[] memo;
// 主函数
public int rob(int[] nums) {
// 初始化备忘录
memo = new int[nums.length];
Arrays.fill(memo, -1);
// 强盗从第 0 间房子开始抢劫
return dp(nums, 0);
}
// 返回 dp[start..] 能抢到的最大值
private int dp(int[] nums, int start) {
if (start >= nums.length) {
return 0;
}
// 避免重复计算
if (memo[start] != -1) return memo[start];
int res = Math.max(dp(nums, start + 1),
nums[start] + dp(nums, start + 2));
// 记入备忘录
memo[start] = res;
return res;
}
int rob(int[] nums) {
int n = nums.length;
// dp[i] = x 表示:
// 从第 i 间房子开始抢劫,最多能抢到的钱为 x
// base case: dp[n] = 0
int[] dp = new int[n + 2];
for (int i = n - 1; i >= 0; i--) {
dp[i] = Math.max(dp[i + 1], nums[i] + dp[i + 2]);
}
return dp[0];
}
dp[i]
最近的两个状态有关,所以可以进一步优化,将空间复杂度降低到 O(1)。
int rob(int[] nums) {
int n = nums.length;
// 记录 dp[i+1] 和 dp[i+2]
int dp_i_1 = 0, dp_i_2 = 0;
// 记录 dp[i]
int dp_i = 0;
for (int i = n - 1; i >= 0; i--) {
dp_i = Math.max(dp_i_1, nums[i] + dp_i_2);
dp_i_2 = dp_i_1;
dp_i_1 = dp_i;
}
return dp_i;
}
House Robber II
nums=[2,3,2]
,算法返回的结果应该是 3 而不是 4,因为开头和结尾不能同时被抢。
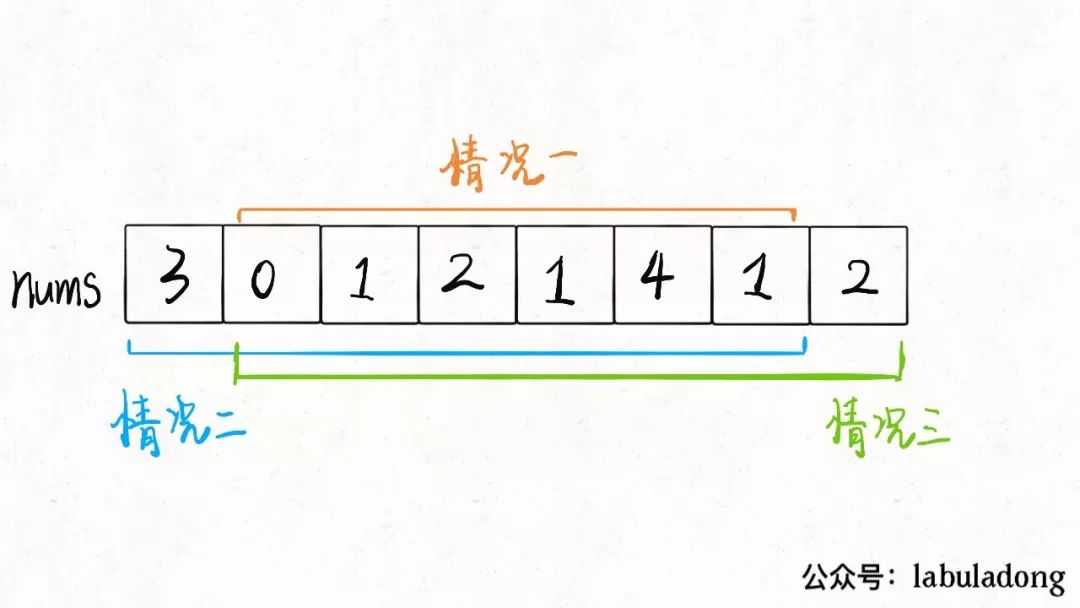
public int rob(int[] nums) {
int n = nums.length;
if (n == 1) return nums[0];
return Math.max(robRange(nums, 0, n - 2),
robRange(nums, 1, n - 1));
}
// 仅计算闭区间 [start,end] 的最优结果
int robRange(int[] nums, int start, int end) {
int n = nums.length;
int dp_i_1 = 0, dp_i_2 = 0;
int dp_i = 0;
for (int i = end; i >= start; i--) {
dp_i = Math.max(dp_i_1, nums[i] + dp_i_2);
dp_i_2 = dp_i_1;
dp_i_1 = dp_i;
}
return dp_i;
}
House Robber III

Map<TreeNode, Integer> memo = new HashMap<>();
public int rob(TreeNode root) {
if (root == null) return 0;
// 利用备忘录消除重叠子问题
if (memo.containsKey(root))
return memo.get(root);
// 抢,然后去下下家
int do_it = root.val
+ (root.left == null ?
0 : rob(root.left.left) + rob(root.left.right))
+ (root.right == null ?
0 : rob(root.right.left) + rob(root.right.right));
// 不抢,然后去下家
int not_do = rob(root.left) + rob(root.right);
int res = Math.max(do_it, not_do);
memo.put(root, res);
return res;
}
N
为数的节点数。
int rob(TreeNode root) {
int[] res = dp(root);
return Math.max(res[0], res[1]);
}
/* 返回一个大小为 2 的数组 arr
arr[0] 表示不抢 root 的话,得到的最大钱数
arr[1] 表示抢 root 的话,得到的最大钱数 */
int[] dp(TreeNode root) {
if (root == null)
return new int[]{0, 0};
int[] left = dp(root.left);
int[] right = dp(root.right);
// 抢,下家就不能抢了
int rob = root.val + left[0] + right[0];
// 不抢,下家可抢可不抢,取决于收益大小
int not_rob = Math.max(left[0], left[1])
+ Math.max(right[0], right[1]);
return new int[]{not_rob, rob};
}
推荐↓↓↓
长
按
关
注
以上是关于经典动态规划:打家劫舍系列问题的主要内容,如果未能解决你的问题,请参考以下文章