一道有关动态规划（Dynamic Programming）的网易面试题

Posted 2021-04-18 机器之禅

最近遇到一道很经典的有关动态规划的网易面试题：

小Q和牛博士合唱一首歌曲,这首歌曲由n个音调组成,每个音调由一个正整数表示。
对于每个音调要么由小Q演唱要么由牛博士演唱,对于一系列音调演唱的难度等于所有相邻音调变化幅度之和, 例如一个音调序列是8, 8, 13, 12, 那么它的难度等于|8 - 8| + |13 - 8| + |12 - 13| = 6(其中||表示绝对值)。
现在要对把这n个音调分配给小Q或牛博士,让他们演唱的难度之和最小,请你算算最小的难度和是多少。
如样例所示: 小Q选择演唱{5, 6}难度为1, 牛博士选择演唱{1, 2, 1}难度为2,难度之和为3,这一个是最小难度和的方案了。

输入描述:

输入包括两行,第一行一个正整数n(1 ≤ n ≤ 2000) 第二行n个整数v[i](1 ≤ v[i] ≤ 10^6), 表示每个音调。

输出描述:

输出一个整数,表示小Q和牛博士演唱最小的难度和是多少。

输入例子1:

5
1 5 6 2 1

输出例子1:

3

这是一道动态规划的题目。

详细很多同学和我一样，一看到动态规划（Dynamic Programming）和拓扑图等名词就头疼，令人纠结的是很多大公司都会考动态规划的题目，好吧！静下心来去弄懂动态规划的算法原理。

动态规划的思想：

若该问题很复杂，我们考虑将问题分为几个小问题，而且这些小问题相互之间不存在相互调用，这就是动态规划的思想。

如下图有五个阶段，每个阶段有4种选择，求最短路径：

我们用暴力搜索方法去求解，共需要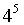次运算，时间复杂度高达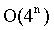，如果面试利用暴力搜索方法去寻找最优问题，应该达不到所设置的运行时间。

我们用动态规划方法去求解，利用递归思想，先计算S1阶段的最短路径，然后保存该路径，利用递归的思想去求解S2，S3，....，S5，这种方法的时间复杂度。所以说动态规划大大的减小了运行时间。

一说到“递归”，我们想到了什么？没错，那就是递归表达式，动态规划算法称其为状态转移方程，思想是一样的。

若我们知道了状态转移方程，且知道初始状态值，那么我们就可以通过递归去求解算法最优问题，切记动态规划算法能够缩短运行时间的原因在于每次递归后保存了该状态的值。

下面我们用动态规划分析这道面试题：

假设dp[i][j]表示一个人选择第i个音调和另一个人选择第j个音调的最小难度，这里不特指小Q和牛博是的原因是这里的 i 永远大于 j。

i大于j共有两种情况：

1）i =j+1时，我们在完全题目的基础下，写下递归关系（即状态转移方程）：

dp[i][j] = dp[i-1][k] + abs(arr[i] - arr[k])    其中 0<=k<i-1

 2）i>=j+1时，递归关系：

dp[i][j] = dp[i-1][j] +  abs(arr[i])-arr[i-1])

我们知道了状态转移方程，还需要设置初始值：

由题意可知，难度计算必须要有两个调才能计算。

因此初始值可设置：dp[0][0] = 0，dp[1][0] = 0；

当i = j+1时，dp[i][j]的递推表达式没考虑到一种特殊情况：当一个人是第一次谈第i个调时，之前的 （i-1）个调都是另一个人谈的，就有 dp[i][j] = abs(arr[1]-arr[0]) + abs(arr[2]-arr[1]) + ... + abs(arr[i-1]-arr[i-2])

根据上面的分析编码：

#include<iostream>
#include<vector>
#include<algorithm>

using namespace std;

int main()
{
	int len=0;

	while(cin >> len)
	{
		vector<int> arr(len);
		for(int i = 0;i < len;i++)
			cin>>arr[i];

		if(len<3)
			cout<<"0"<<endl;
		else
		{
			//vector<vector<int>> dp(len,len);
			vector<vector<int>> dp(len,vector<int>(len));
			vector<int> acc(len);

			//dp[0][0] = 0 - abs(arr[1] - arr[0]);
			dp[0][0] = 0;

			for(int i = 1;i < len;i++)
			{
				acc[i] = acc[i-1] + abs(arr[i] - arr[i-1]);
				dp[i][i-1] = acc[i-1];
				for(int j = 0;j<i-1;j++){
					dp[i][j] = dp[i-1][j] + acc[i] - acc[i-1];
					dp[i][i-1] = min(dp[i][i-1],dp[i-1][j] + abs(arr[i]-arr[j]));
				}
			}

			int min1 = 1e9;
			for(int j =0;j<len-1;j++){
				min1 = min(min1,dp[len-1][j]);
			}
			cout<<min1<<endl;
		}

	}
	return 0;
}

代码和解题思路参考了网友buaaqlyj的回答：

https://www.nowcoder.com/test/question/done?tid=30725143&qid=126954#summary

欢迎扫码关注：