动态规划入门看这篇就够了,万字长文!
Posted 小浩算法
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了动态规划入门看这篇就够了,万字长文!相关的知识,希望对你有一定的参考价值。

今天是小浩算法 “365刷题计划” 动态规划 - 整合篇。大家应该期待已久了吧!奥利给!

我们把要解决的一个大问题转换成若干个规模较小的同类型问题,当我们求解出这些小问题的答案,大问题便不攻自破。同时,在求解这些小问题的过程中,我们把需要重复计算的答案记录下来放在数组中,下次如果遇到同样的小问题需要计算,便直接查询出结果。这就是动态规划。
很多人觉得DP难(下文统称动态规划为DP),根本原因是因为DP区别于一些固定形式的算法(如 DFS、二分法、KMP),没有固定的步骤规定第一步第二步来做什么。所以我觉得DP更应该被看作为一种解决问题的思想。这种思想的本质是:一个规模较大的问题(可以用两三个参数表示),通过若干规模较小的问题的结果来得到的(通常会寻求到一些特殊的计算逻辑,如求最值等)
讲解动态规划的资料很多,官方的定义是指把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解。概念中的各阶段之间的关系,其实指的就是状态转移方程。
我们一般看到的状态转移方程,基本长成下面这样(注:i、j、k 都是在定义DP方程中用到的参数。opt 指代特殊的计算逻辑,大多数情况下为 max 或 min。func 指代逻辑函数):
dp[i] = opt(dp[i-1])+1
dp[i][j] = func(i,j,k) + opt(dp[i-1][k])
dp[i][j] = opt(dp[i-1][j-1],dp[i-1][j])+arr[i][j]
dp[i][j] = opt(dp[i-1][j] + xi, dp[i][j-1] + yj, ...)
....等等
到这里估计大家要懵逼了,这特么都是些啥玩意。先别着急叉掉这个页面,听我慢慢说来。状态转移方程,说白了是用来描述大规模问题和小规模问题之间的关系。既然是关系,那肯定就不是唯一的,抽象的,形式化的东西。可以用小拇指想想,世界上关系那么多,你怎么可能全部能记得住。所以我个人并不建议去死记硬背各种类型的状态转移方程。脱离了应用场景的公式,全部都是耍流氓,生搬硬套的结果一定是四不像。既然如此,那DP的题型就完全无法掌握吗?我认为不是。在本节中,我们将通过5道题目,带着大家由浅入深学习一下动态规划的核心思想。

我们先通过一道最简单的DP题目,熟悉DP的概念。
第70题:假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入:2 输出:2 解释:有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
示例 2:
输入:3 输出:3 解释:有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
首先我们分析本题,该题满足“大问题由小问题的结果产生”的条件:
上 1 阶台阶:有 1 种方式
上 2 阶台阶:有 1+1 和 2 两种方式
上 3 阶台阶:我们只能从第 2 阶或者第 1 阶 到达第 3 阶,所以到达第 3 阶的方法总数就是到第 1 阶和第 2 阶的方法数之和。
上 n 阶台阶:我们只能从第 n-1 阶或者第 n-2 阶 到达第 n 阶,所以到达第 n 阶的方法总数就是到第 n-1 阶和第 n-2 阶的方法数之和。
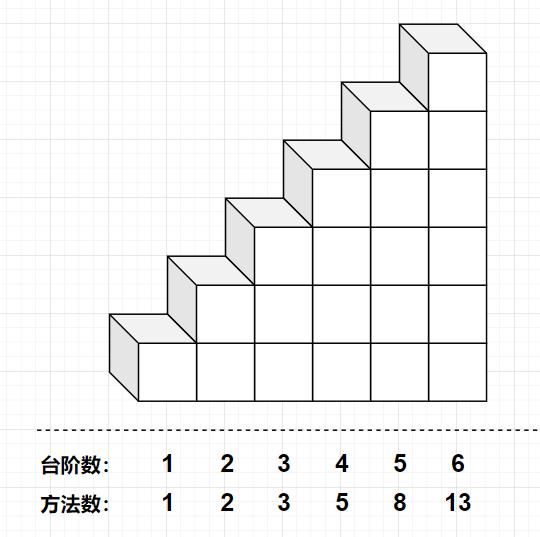
“大问题由小问题的结果产生”,我们也可以换个专业点的说法:即该问题的最优解可以从其子问题的最优解来进行构建。我们令 dp[n] 表示到达第 n 阶的方法总数。可以得到如下状态转移方程(如果不明白,可以认真看一下上面的图):
dp[n]=dp[n-1]+dp[n-2]
根据分析,得出代码:(Go语言)
1func climbStairs(n int) int {
2 if n == 1 {
3 return 1
4 }
5 dp := make([]int, n+1)
6 dp[1] = 1
7 dp[2] = 2
8 for i := 3; i <= n; i++ {
9 dp[i] = dp[i-1] + dp[i-2]
10 }
11 return dp[n]
12}
在上文中,我们讲解了DP的概念并且通过示例进行了学习。现在我们继续通过一道简单例题,来加强大家的理解。
第53题:给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
示例:
输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大,为 6。
动态规划第一步:定义状态。对于本题如何定义状态?我们分析题目,一个连续子数组一定要以一个数作为结尾,那是不是可以定义dp[i] 表示以 nums[i] 结尾的连续子数组的最大和。为啥要这样定义?如果要得到dp[i],那么nums[i]一定会被选取。并且 dp[i] 所表示的连续子序列与 dp[i-1] 所表示的连续子序列很可能就差一个 nums[i],当然这是在dp[i-1]大于0的情况下。公式是这样:
dp[i] = dp[i-1]+nums[i] , if (dp[i-1] >= 0)
自然,dp[i-1]也是有可能小于0的,此时dp[i]的值就是nums[i]了。
dp[i] = nums[i] , if (dp[i-1] < 0)
通过上面的分析,我们可以得出状态转移方程:
dp[i]=max(nums[i], dp[i−1]+nums[i])
得到了状态转移方程,但是我们还需要通过一个已有的状态的进行推导,我们可以想到 dp[0] 一定是以 nums[0] 进行结尾。所以对dp[0]进行初始化:
dp[0] = nums[0]
问题来了,最终的答案是啥?在很多题目中,因为dp[i]本身就定义成了题目中的问题,所以dp[i]最终就是要的答案。但是对于本题,这里定义的状态,并不是题目中要求解的问题,所以不能直接返回最后的一个状态 (这一步经常有初学者会摔跟头)。那最终答案是啥呢?其实我们是寻找:
max(dp[0], dp[1], ..., d[i-1], dp[i])
干巴巴的说了半天,我们绘制成图可能更容易理解:
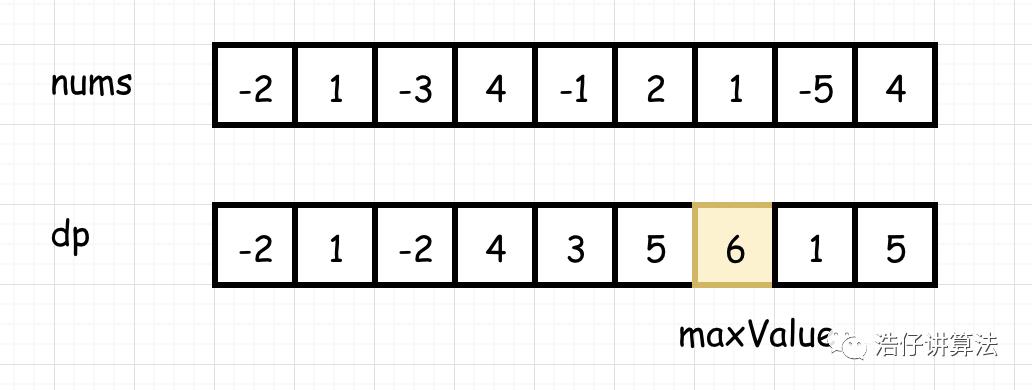
根据分析,得出代码:
1func maxSubArray(nums []int) int {
2 if len(nums) < 1 {
3 return 0
4 }
5 dp := make([]int, len(nums))
6 //设置初始化值
7 dp[0] = nums[0]
8 for i := 1; i < len(nums); i++ {
9 //处理 dp[i-1] < 0 的情况
10 if dp[i-1] < 0 {
11 dp[i] = nums[i]
12 } else {
13 dp[i] = dp[i-1] + nums[i]
14 }
15 }
16 result := -1 << 31
17 for _, k := range dp {
18 result = max(result, k)
19 }
20 return result
21}
22
23func max(a, b int) int {
24 if a > b {
25 return a
26 }
27 return b
28}
进一步精简代码:
1func maxSubArray(nums []int) int {
2 if len(nums) < 1 {
3 return 0
4 }
5 dp := make([]int, len(nums))
6 result := nums[0]
7 dp[0] = nums[0]
8 for i := 1; i < len(nums); i++ {
9 dp[i] = max(dp[i-1]+nums[i], nums[i])
10 result = max(dp[i], result)
11 }
12 return result
13}
14
15func max(a, b int) int {
16 if a > b {
17 return a
18 }
19 return b
20}
这个例子是为了告诉大家:状态的定义并不一定是最终求解的问题答案,自然也就不能想当然的到最后返回一个dp[i]就觉得完事,具体问题具体分析,把握住状态的含义才是核心。(谨记)

前面两道题,相信大家对DP已不陌生,本题将增加一定难度。(越短越难有木有)
第300题:给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
首先我们分析题目,要找的是最长上升子序列(Longest Increasing Subsequence,LIS)。因为题目中没有要求连续,所以LIS可能是连续的,也可能是非连续的。同时,LIS符合可以从其子问题的最优解来进行构建的条件。所以我们可以尝试用动态规划来进行求解。首先我们定义状态:dp[i] 表示以nums[i]结尾的最长上升子序列的长度。我们假定nums为[1,9,5,9,3]:
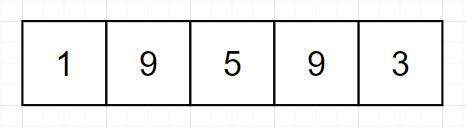
我们初步可以得到下面的结论:
如果nums[i]比前面的所有元素都小,那么dp[i]等于1(即它本身)(该结论正确)
如果nums[i]前面存在比他小的元素nums[j],那么dp[i]就等于dp[j]+1(该结论错误,比如nums[3]>nums[0],即9>1,但是dp[3]并不等于dp[0]+1)
为什么第二个结论错误?因为dp[i]前面比他小的元素,不一定只有一个!可能除了nums[j],还包括nums[k],nums[p] 等等等等。所以dp[i]除了可能等于dp[j]+1,还有可能等于dp[k]+1,dp[p]+1 等等等等。所以我们求dp[i],需要找到dp[j]+1,dp[k]+1,dp[p]+1 等等等等 中的最大值。(初学者极易在这里摔跟头)我们可以得到下面的状态转移公式:
dp[i] = max(dp[j]+1,dp[k]+1,dp[p]+1,.....)
条件:
nums[i] > nums[j]
nums[i] > nums[k]
nums[i] > nums[p]
如果不能理解,可以看下面这个图:
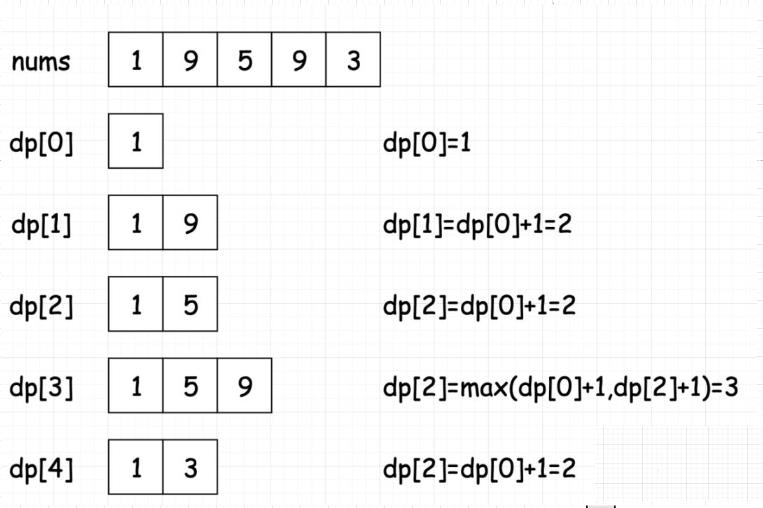
最后我们只需要找DP数组中的最大值即可,代码如下:
1func lengthOfLIS(nums []int) int {
2 if len(nums) < 1 {
3 return 0
4 }
5 dp := make([]int, len(nums))
6 result := 1
7 for i := 0; i < len(nums); i++ {
8 dp[i] = 1
9 for j := 0; j < i; j++ {
10 //这行代码就是上文中那个 等等等等
11 if nums[j] < nums[i] {
12 dp[i] = max(dp[j]+1, dp[i])
13 }
14 }
15 result = max(result, dp[i])
16 }
17 return result
18}
19
20func max(a, b int) int {
21 if a > b {
22 return a
23 }
24 return b
25}
这道题目相比上面两道题难度有所提升,但其解题思想与上面两题如出一辙,请大家认真思考。

在上文中,我们通过题目“最长上升子序列”以及"最大子序和",学习了DP在线性关系中的分析方法。这种分析方法,在运筹学中也被称为“线性动态规划”,当然这点大家作为了解即可。现在我们将分享一道略微区别于前面三道题的类型。
第120题:给定一个三角形,找出自顶向下的最小路径和。
每一步只能移动到下一行中相邻的结点上。
例如,给定三角形:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
不少人在这道题目上栽过跟头,一起分析一下。首先我们要找的是三角形最小路径和,总得知道这是个啥意思。假设我们有一个三角形:[[2], [3,4], [6,5,7], [4,1,8,3]],长这样:
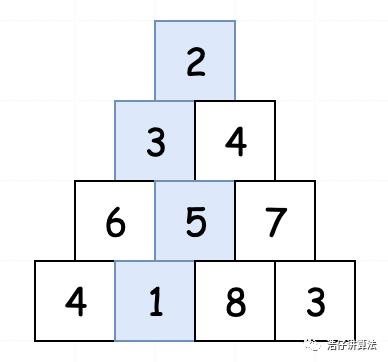
那从上到下的最小路径和就是2-3-5-1,等于11。由于我们是使用数组来定义一个三角形,所以便于我们分析,我们将三角形稍微进行改动:
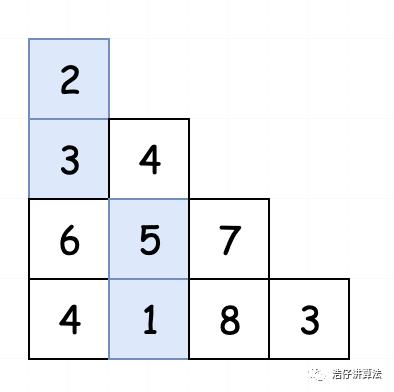
相当于我们将整个三角形进行了拉伸。这时候,我们根据题目中给出的条件:每一步只能移动到下一行中相邻的结点上。其实也就等同于,每一步我们只能往下移动一格或者右下移动一格。将其转化成代码,假如2所在的元素位置为[0,0],那我们往下移动就只能移动到[1,0]或者[1,1]的位置上。假如5所在的位置为[2,1],同样也只能移动到[3,1]和[3,2]的位置上。如下图所示:
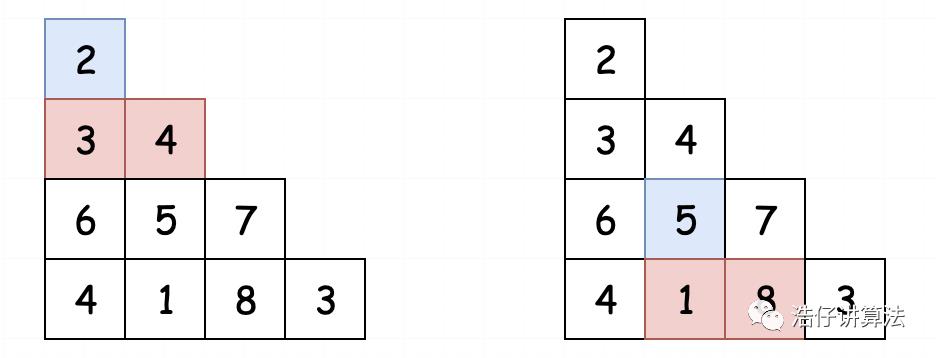
明确了题目,我们开始分析。题目很明显满足可以从子问题的最优解进行构建的条件,所以我们考虑通过动态规划进行求解。老样子,我们先定义状态:
dp[i][j] : 表示包含第i行j列元素的最小路径和
我们很容易想到可以自顶向下进行分析。并且,无论最后的路径是哪一条,它一定要经过最顶上的元素,即[0,0]。所以我们需要对dp[0][0]进行初始化。
dp[0][0] = [0][0]位置所在的元素值
继续分析,如果我们要求dp[i][j],那么其一定会从自己头顶上的两个元素移动而来。啥意思:
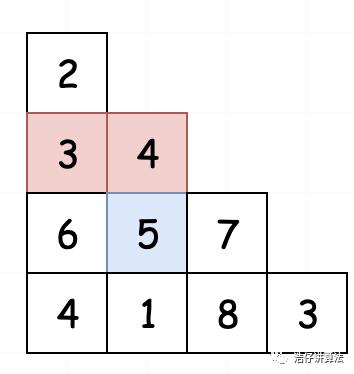
如5这个位置的最小路径和,要么是从2-3-5而来,要么是从2-4-5而来。然后取两条路径和中较小的一个即可。进而我们得到状态转移方程:
dp[i][j] = min(dp[i-1][j-1],dp[i-1][j]) + triangle[i][j]
但是,我们这里会遇到一个问题!除了最顶上的元素之外,
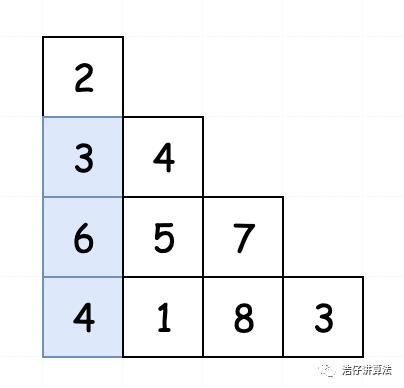
最左边的元素只能从自己头顶而来。(2-3-6-4)
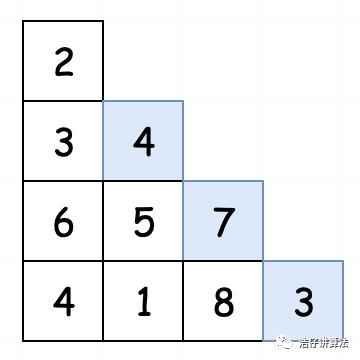
最右边的元素只能从自己左上角而来。(2-4-7-3)
同时,我们观察到,位于第2行的元素,都是特殊元素(因为都只能从[0,0]的元素走过来),我们可以直接将其特殊处理,得到:
dp[1][0] = triangle[1][0] + triangle[0][0]
dp[1][1] = triangle[1][1] + triangle[0][0]
最后,我们只要找到最后一行元素中,路径和最小的一个,就是我们的答案。即(l为dp数组长度):
result = min(dp[l-1,0],dp[l-1,1],dp[l-1,2]....)
综上我们就分析完了,我们总共进行了4步:
定义状态
总结状态转移方程
分析状态转移方程不能满足的特殊情况。
得到最终解
根据分析,得出代码:
1//未优化内存版本
2func minimumTotal(triangle [][]int) int {
3 if len(triangle) < 1 {
4 return 0
5 }
6 if len(triangle) == 1 {
7 return triangle[0][0]
8 }
9 dp := make([][]int, len(triangle))
10 for i, arr := range triangle {
11 dp[i] = make([]int, len(arr))
12 }
13
14 result := 2 << 31 + 1
15 dp[0][0] = triangle[0][0]
16 dp[1][1] = triangle[1][1] + triangle[0][0]
17 dp[1][0] = triangle[1][0] + triangle[0][0]
18
19 for i := 2; i < len(triangle); i++ {
20 for j := 0; j < len(triangle[i]); j++ {
21 if j == 0 {
22 dp[i][j] = dp[i-1][j] + triangle[i][j]
23 } else if j == (len(triangle[i]) - 1) {
24 dp[i][j] = dp[i-1][j-1] + triangle[i][j]
25 } else {
26 dp[i][j] = min(dp[i-1][j-1], dp[i-1][j]) + triangle[i][j]
27 }
28 }
29 }
30 for _,k := range dp[len(dp)-1] {
31 result = min(result, k)
32 }
33 return result
34}
35
36func min(a, b int) int {
37 if a > b {
38 return b
39 }
40 return a
41}

运行上面的代码,我们发现使用的内存过大。我们有没有什么办法可以压缩内存呢?通过观察我们发现,在我们自顶向下的过程中,其实我们只需要使用到上一层中已经累积计算完毕的数据,并且不会再次访问之前的元素数据。绘制成图如下:
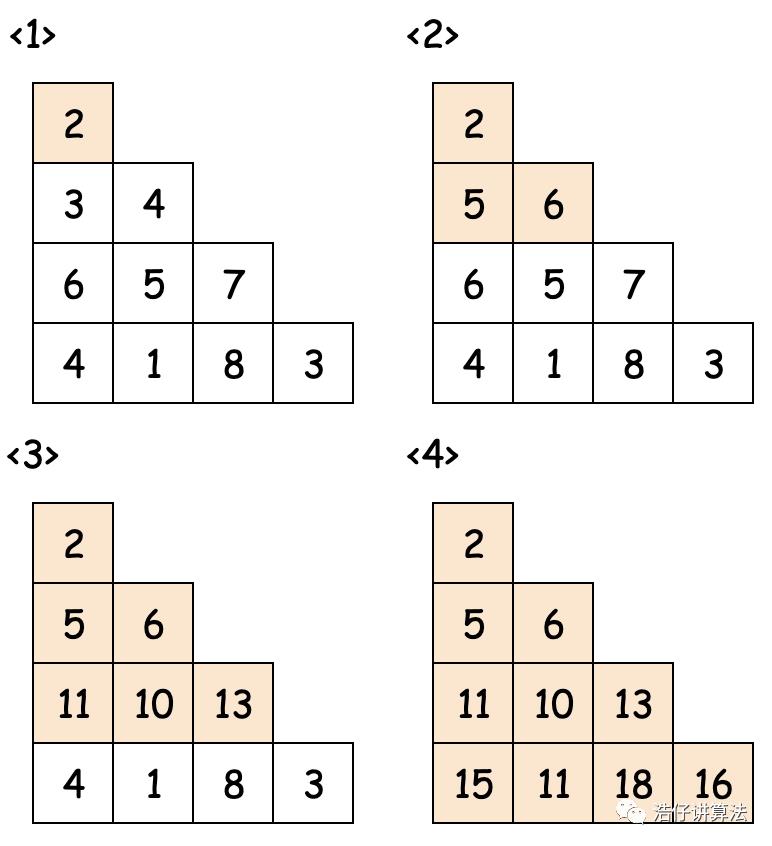
所以我们可以优化代码:
1//优化版本
2func minimumTotal(triangle [][]int) int {
3 l := len(triangle)
4 if l < 1 {
5 return 0
6 }
7 if l == 1 {
8 return triangle[0][0]
9 }
10 result := 1<<31 - 1
11 triangle[0][0] = triangle[0][0]
12 triangle[1][1] = triangle[1][1] + triangle[0][0]
13 triangle[1][0] = triangle[1][0] + triangle[0][0]
14 for i := 2; i < l; i++ {
15 for j := 0; j < len(triangle[i]); j++ {
16 if j == 0 {
17 triangle[i][j] = triangle[i-1][j] + triangle[i][j]
18 } else if j == (len(triangle[i]) - 1) {
19 triangle[i][j] = triangle[i-1][j-1] + triangle[i][j]
20 } else {
21 triangle[i][j] = min(triangle[i-1][j-1], triangle[i-1][j]) + triangle[i][j]
22 }
23 }
24 }
25 for _,k := range triangle[l-1] {
26 result = min(result, k)
27 }
28 return result
29}
30
31func min(a, b int) int {
32 if a > b {
33 return b
34 }
35 return a
36}

可以看到现在内存极大的进行了优化。总结一下,这道题的难度是比前面几道题大的,但是还是可以按部就班的进行分析。当然,在分析的过程中,本题我们引入了一个技巧:根据每次计算只会访问前一次计算结果的特性,我们把原数组直接当成了DP数组来进行使用。(同时,本题其实还可以自下而上进行分析,大家可以下去尝试一下)

在上文中,我们通过分析,顺利完成了“三角形最小路径和”的动态规划题解。在本节中,我们继续看一道相似题型,以求能完全掌握这种“路径和”问题。
第64题:给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
上一题是三角形,这一道题换成了矩形,是不是可以直接“抄”上面的分析过程呢?分析一下,要找的是 最小路径和,这是个啥意思呢?假设我们有一个 m*n 的矩形 :[[1,3,1],[1,5,1],[4,2,1]]
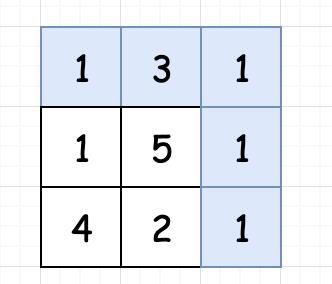
那从左上角到右下角的最小路径和,我们可以很容易看出就是1-3-1-1-1,这一条路径,结果等于7。
明确题目后继续分析,该题与上一道求三角形最小路径和一样,题目符合可以从子问题的最优解进行构建,所以我们考虑使用动态规划进行求解。首先,我们定义状态:
dp[i][j] : 表示包含第i行j列元素的最小路径和
同样,因为任何一条到达右下角的路径,都会经过[0,0]这个元素。所以我们需要对dp[0][0]进行初始化。
dp[0][0] = [0][0]位置所在的元素值
继续分析,根据题目给的条件,如果我们要求dp[i][j],那么它一定是从自己的上方或者左边移动而来。如下图所示:
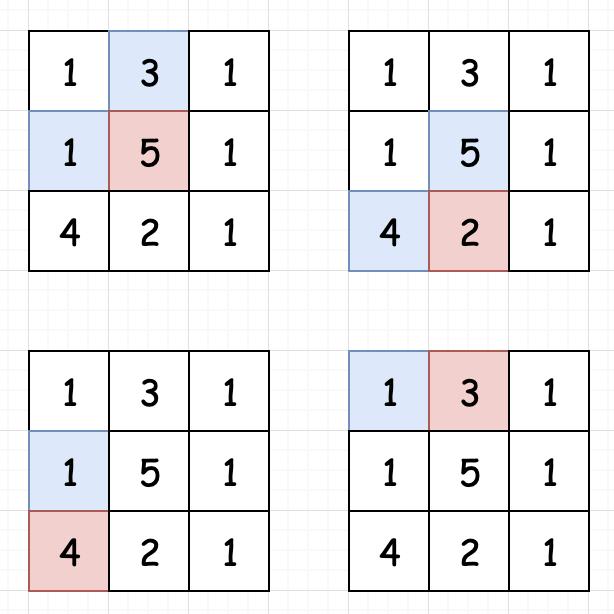
5,只能从3或者1移动而来
2,只能从5或者4移动而来
4,从1移动而来
3,从1移动而来
(红色位置必须从蓝色位置移动而来)
进而我们得到状态转移方程:
dp[i][j] = min(dp[i-1][j],dp[i][j-1]) + grid[i][j]
同样我们需要考虑两种特殊情况:
最上面一行,只能由左边移动而来(1-3-1)
最左边一列,只能由上面移动而来(1-1-4)
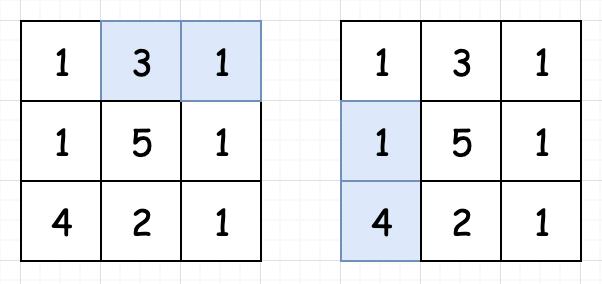
最后,因为我们的目标是从左上角走到右下角,整个网格的最小路径和其实就是包含右下角元素的最小路径和。即:
设:dp的长度为l
最终结果就是:dp[l-1][len(dp[l-1])-1]
综上我们就分析完了,我们总共进行了4步:
定义状态
总结状态转移方程
分析状态转移方程不能满足的特殊情况。
得到最终解
根据分析,得出题解:
1//原始版本
2func minPathSum(grid [][]int) int {
3 l := len(grid)
4 if l < 1 {
5 return 0
6 }
7 dp := make([][]int, l)
8 for i, arr := range grid {
9 dp[i] = make([]int, len(arr))
10 }
11 dp[0][0] = grid[0][0]
12 for i := 0; i < l; i++ {
13 for j := 0; j < len(grid[i]); j++ {
14 if i == 0 && j != 0 {
15 dp[i][j] = dp[i][j-1] + grid[i][j]
16 } else if j == 0 && i != 0 {
17 dp[i][j] = dp[i-1][j] + grid[i][j]
18 } else if i !=0 && j != 0 {
19 dp[i][j] = min(dp[i-1][j], dp[i][j-1]) + grid[i][j]
20 }
21 }
22 }
23 return dp[l-1][len(dp[l-1])-1]
24}
25
26func min(a, b int) int {
27 if a > b {
28 return b
29 }
30 return a
31}

事实总是惊人的相似,运行上面的代码,内存又过大了。有没有什么办法可以压缩内存呢?同样的方法,在我们自左上角到右下角计算各个节点的最小路径和的过程中,我们只需要使用到之前已经累积计算完毕的数据,并且不会再次访问之前的元素数据。绘制成图如下:
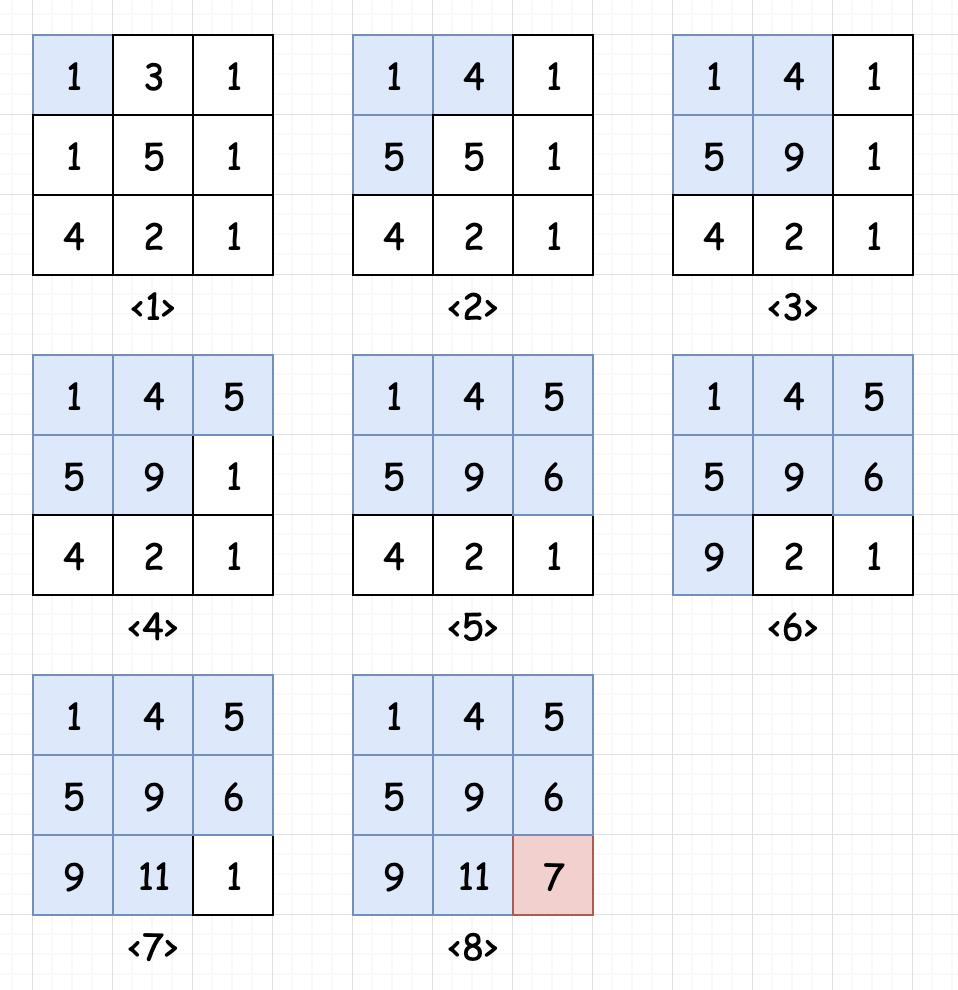
优化后的代码如下:
1//优化版本
2func minPathSum(grid [][]int) int {
3 l := len(grid)
4 if l < 1 {
5 return 0
6 }
7 for i := 0; i < l; i++ {
8 for j := 0; j < len(grid[i]); j++ {
9 if i == 0 && j != 0 {
10 grid[i][j] = grid[i][j-1] + grid[i][j]
11 } else if j == 0 && i != 0 {
12 grid[i][j] = grid[i-1][j] + grid[i][j]
13 } else if i !=0 && j != 0 {
14 grid[i][j] = min(grid[i-1][j], grid[i][j-1]) + grid[i][j]
15 }
16 }
17 }
18 return grid[l-1][len(grid[l-1])-1]
19}
20
21func min(a, b int) int {
22 if a > b {
23 return b
24 }
25 return a
26}


通过上文的学习,相信大家已经对DP有所了解。这道题将回归一道简单问题,和大家探究一个疑惑:如果状态定义出错,会出现什么问题?
第198题:你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。
给定一个代表每个房屋存放金额的非负整数数组,计算你在不触动警报装置的情况下,能够偷窃到的最高金额。
示例 1:
输入: [1,2,3,1]
输出: 4
解释: 偷窃 1 号房屋 (金额 = 1) ,然后偷窃 3 号房屋 (金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 2:
输入: [2,7,9,3,1]
输出: 12
解释: 偷窃 1 号房屋 (金额 = 2), 偷窃 3 号房屋 (金额 = 9),接着偷窃 5 号房屋 (金额 = 1)。
偷窃到的最高金额 = 2 + 9 + 1 = 12 。
上面的题目,我们第一步都是先定义状态。只要定义好了状态,同时分析出状态转移方程,一般就可以流畅的解决问题了。但是如果状态定义出错会发生什么呢?我们尝试一下:假设有i间房子,我们可能会定义出两种状态:
dp[i] : 偷盗 含 第i个房子时,所获取的最大利益
dp[i] : 偷盗 至 第i个房子时,所获取的最大利益
如果我们定义为状态一,因为我们没办法知道获取最高金额时,小偷到底偷盗了哪些房屋。所以我们需要找到所有状态中的最大值,才能找到我们的最终答案。即:
max(dp[0],dp[1],.....,dp[len(dp)-1])
如果我们定义为状态二,因为小偷一定会从前偷到最后(强调:偷盗至第i个房间,不代表小偷要从第i个房间中获取财物)。所以我们的最终答案很容易确定。即:
dp[i]
现在我们分析这两种状态定义下的状态转移方程:
如果是状态一,偷盗含第i个房间时能获取的最高金额,我们相当于要找到偷盗每一间房子时可以获取到的最大金额。比如下图,我们要找到dp[4],也就是偷盗9这间房子时,能获取到的最大金额。

那我们就需要找到与9不相邻的前后两段中能获取到的最大金额。

我们发现题目进入恶性循环,因为我们若要找到与9不相邻的两端中能偷盗的最大金额,根据dp[i]的定义,我们就又需要分析在这两段中盗取每一间房子时所能获取的最大利益!想想都很可怕!所以我们放弃掉这种状态的定义。
如果是状态二,偷盗至第i个房子时,所能获取的最大利益。那我们可以想到,由于不可以在相邻的房屋闯入,所以 至i房屋可盗窃的最大值,要么就是至 i-1 房屋可盗窃的最大值,要么就是至 i-2 房屋可盗窃的最大值加上当前房屋的值,二者之间取最大值。即:
dp[i] = max(dp[i-2]+nums[i], dp[i-1])
如果不能理解可以看下图:
(相当于小贼背了个背包,里边装了之前偷来的财物,每到达下一个房间门口,来选择是偷还是不偷。)
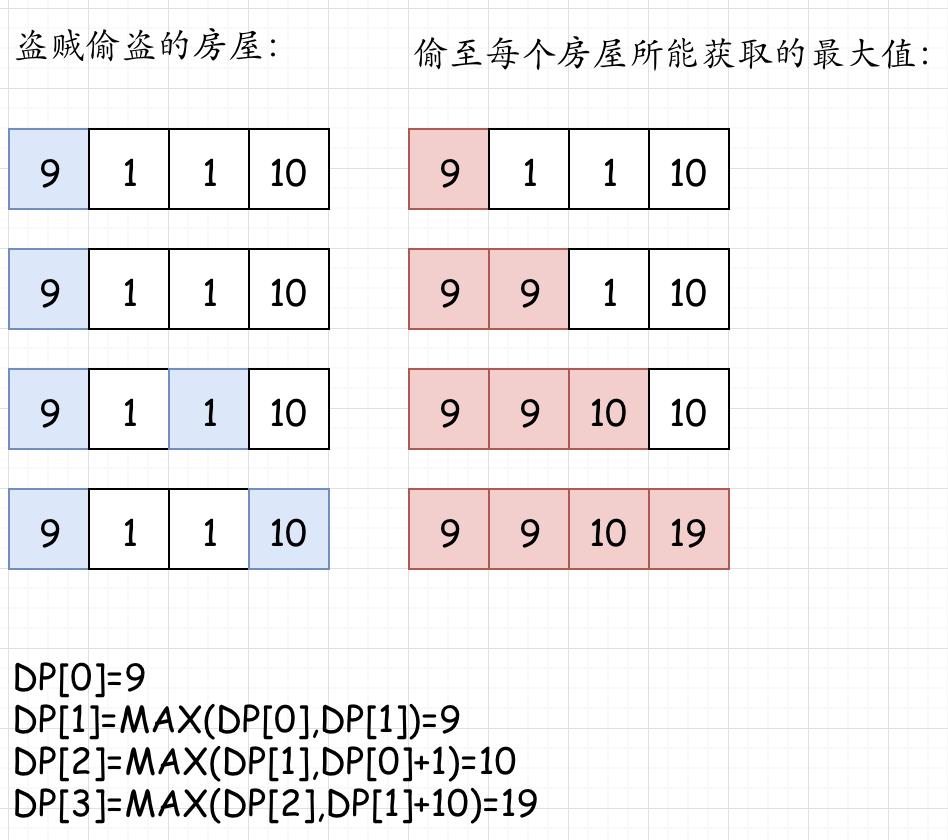
1func rob(nums []int) int {
2 if len(nums) < 1 {
3 return 0
4 }
5 if len(nums) == 1 {
6 return nums[0]
7 }
8 if len(nums) == 2 {
9 return max(nums[0],nums[1])
10 }
11 dp := make([]int, len(nums))
12 dp[0] = nums[0]
13 dp[1] = max(nums[0],nums[1])
14 for i := 2; i < len(nums); i++ {
15 dp[i] = max(dp[i-2]+nums[i],dp[i-1])
16 }
17 return dp[len(dp)-1]
18}
19
20func max(a,b int) int {
21 if a > b {
22 return a
23 }
24 return b
25}

内存又大了?还是一样优化方法,小贼偷盗的过程中,不可能转回头去到自己已经偷过的房间!(太蠢)小偷只需要每次将财物搬到下一个房间就行!
根据上面思路,优化后的代码如下:
1func rob(nums []int) int {
2 if len(nums) < 1 {
3 return 0
4 }
5 if len(nums) == 1 {
6 return nums[0]
7 }
8 if len(nums) == 2 {
9 return max(nums[0],nums[1])
10 }
11 nums[1] = max(nums[0],nums[1])
12 for i := 2; i < len(nums); i++ {
13 nums[i] = max(nums[i-2]+nums[i],nums[i-1])
14 }
15 return nums[len(nums)-1]
16}
17
18func max(a,b int) int {
19 if a > b {
20 return a
21 }
22 return b
23}
动态规划入门整合系列篇到这里就完事了,相信大家如果可以完整看完,一定会有所收获。但是呢,其实大家可以看到,上面的系列还有很多内容没有讲:比如状态压缩,背包问题 等等。后面我的计划是单独拎出来一个 背包系列篇 以及 动态规划高级篇系列。
今天的整合篇去除了之前的一些冗余内容,对部分图解也进行了重构,熬夜整合,猝死边缘。如果大家觉得有收获,希望可以转发支持!如果想看我的其他算法文章的,可以看:
如果你问我对学习算法有什么建议,可以看:
小浩算法,每日一题
关注领取《图解算法》高清版
进群的小伙伴请加右侧私人微信(备注:进群)
以上是关于动态规划入门看这篇就够了,万字长文!的主要内容,如果未能解决你的问题,请参考以下文章